C/C++程序开发（08）：一个入门级的TSP路径优化程序

需求描述：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。

---

实现算法：设计变邻域搜索算法计算TSP的最短路径

---

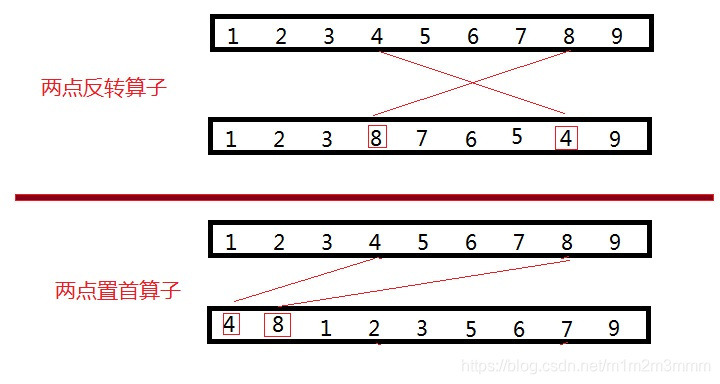
设计算子：

---

代码实现：

（1）头文件vns.h

#include <iostream>
#include <cstdio>
#include <string>
#include <fstream>
#include <vector>
#include <algorithm>
#include <iterator>
#include <valarray>

using namespace std;

struct point{
	double x;
	double y;
};

struct solution{
	vector<int> citiesCode; //城市编码序列
	double pathLength;
};

//输出结果序列
void outputSol(const solution sol);


//得到城市坐标：从外部文件中获取城市坐标信息
int getCitiesCoor(string filePath, vector<point>& citiesCoordinate);
//得到城市矩阵
double* getDistanceMat(const vector<point> citiesCoordinate);

//生成随机客户
vector<int> generateInitPath(int cityCnt);

//得到路径长度
double getPathLength(double* disMat, vector<int> cityCode);

//生成初始解
solution generateIniSol(int cityCnt, double* disMat);

//变邻域搜索函数
solution variableNeighborhoodSearch(solution iniSol, double* disMat);

//梯度下降递减函数
void vnsDescent(solution& sol, double* disMat, int cnt);

//两点反转算子
solution operator2inverse(solution sol, double* disMat);
double getPathReduceCost(vector<int> oldCitiesCode, vector<int> newCitiesCode, double* disMat);
vector<int> get2InverseSerize(int pt1,int pt2, vector<int> citiesCode, double* disMat);

//两点置首算子
solution operator2header(solution& sol, double* disMat);
//得到两点置首后的新序列
vector<int> get2HeaderSerize(int pt1,int pt2, vector<int> citiesCode, double* disMat);

//剔除向量中重复序列,且保持原有序列的顺序
vector<int> delRepetitiveSequence(vector<int> oldSeq);

//扰动函数--分块乱序重组函数（建议为城市个数的因子）
vector<int> shaking(solution inisol, int blockCnt);

（2）源文件vns.cpp

#include "vns.h"

void outputSol(const solution sol)
{
	cout << "路径序列为：" << endl;
	for(vector<int>::const_iterator it = sol.citiesCode.begin(); it != sol.citiesCode.end(); it++)
	{
		cout << *it << " ";
	}
	cout << "\n路径长度：" << sol.pathLength << endl;
}

int getCitiesCoor(string filePath, vector<point>& citiesCoordinate)
{
	ifstream input(filePath);
	string line;
	point pt;
	while(getline(input, line))
	{
		//使用逗号进行字符串分割
		pt.x = atof(line.substr(0, line.find(',')).c_str());
		pt.y = atof(line.substr(line.find(',') + 1, line.length()).c_str());
		citiesCoordinate.push_back(pt);
	}
	return citiesCoordinate.size();
}

//得到城市矩阵
double* getDistanceMat(const vector<point> citiesCoordinate)
{
	int cityCnt = citiesCoordinate.size();
	double* distance = new double[cityCnt * cityCnt];
	for(int i = 0; i < cityCnt; i++)
	{
		for(int j = 0; j < cityCnt; j++)
		{
			distance[i * cityCnt + j] = sqrt(pow(citiesCoordinate[i].x - citiesCoordinate[j].x, 2.0) + 
				pow(citiesCoordinate[i].y - citiesCoordinate[j].y, 2.0));
		}
	}
	return distance;
}

//生成随机客户
vector<int> generateInitPath(int cityCnt)
{
	vector<int> cityCode;
	for(int i = 0; i < cityCnt; i++)
	{
		cityCode.push_back(i);
	}
	random_shuffle(cityCode.begin(), cityCode.end());
	return cityCode;
}

//得到路径长度
double getPathLength(double* disMat, vector<int> cityCode)
{
	double pathLength = disMat[*(cityCode.begin()) * cityCode.size() + *(cityCode.end() - 1)];
	for(vector<int>::iterator it = cityCode.begin(); it != cityCode.end() - 1; it++)
	{
		double tmp = disMat[*it * cityCode.size() + *(it + 1)];
		pathLength += tmp;
	}
	return pathLength;
}
//生成初始解
solution generateIniSol(int cityCnt, double* disMat)
{
	solution tmp = {generateInitPath(cityCnt), getPathLength(disMat, generateInitPath(cityCnt))};
	return tmp;
}

//变邻域搜索函数
solution variableNeighborhoodSearch(solution iniSol, double* disMat)
{
	//初始化分块数
	solution vnsSol;
	int blockCnt = 13;
	vector<int> newCitiesCode = shaking(iniSol, blockCnt);
	double newPathLength = getPathLength(disMat, newCitiesCode);
	solution newSol = {newCitiesCode, newPathLength};
	int iter = 0, cnt = 0;
	while(iter < 10)
	{
		cnt = rand() % 2;
		vnsDescent(newSol, disMat, cnt);	
		iter++;
	}
	return newSol;
}

//梯度下降递减函数
void vnsDescent(solution& sol, double* disMat, int cnt)
{
	solution curSol = sol;
	int count = 0;
	switch(cnt)
	{
	case 0:
		//两点反转算子
		cout << "正在执行两点反转算子" << endl;
		while(count < 5)
		{
			curSol = operator2inverse(sol, disMat);
			if(curSol.pathLength < sol.pathLength)
			{
				sol = curSol;
				cout << "当前解："<< sol.pathLength << endl;
			}else
			{
				count++;			
			}
		}
		break;
	case 1:
		//两点置首算子
		cout << "正在执行两点置首算子" << endl;
		curSol = operator2header(sol, disMat);
		while(count < 5)
		{
			curSol = operator2header(sol, disMat);
			if(curSol.pathLength < sol.pathLength)
			{
				sol = curSol;
				cout << "当前解："<< sol.pathLength << endl;
			}else
			{
				count++;				
			}
		}	
		break;
	}
}

//两点反转算子
solution operator2inverse(const solution sol, double* disMat)
{
	int citiesCnt = sol.citiesCode.size();
	double* tmp = new double[citiesCnt * citiesCnt];
	//计算路径反转节约量
	for(int i = 0; i < citiesCnt - 1; i++)
	{
		for(int j = i + 1; j < citiesCnt; j++)
		{
			double temp = getPathReduceCost(sol.citiesCode,get2InverseSerize(i,j, sol.citiesCode, disMat), disMat);
			tmp[i * citiesCnt + j] = temp;
		}
	}
	int len = citiesCnt * citiesCnt - 1;
	double max = *max_element(tmp, tmp + len);
	int index = distance(tmp, max_element(tmp, tmp + len));
	vector<int> curBestSerize = get2InverseSerize(index / citiesCnt,index % citiesCnt, sol.citiesCode, disMat);
	solution curBestSol = {curBestSerize, getPathLength(disMat, curBestSerize)};
	delete[] tmp; tmp = NULL;
	return curBestSol;
	//
	/*int cnt = 0;
	solution curCitiesCode;
	while()
	{
		cnt++;
		for(int i = 0; i < citiesCnt; i++)
		{
			for(int j = 0; j < citiesCnt; j++)
			{
				if(tmp[i * citiesCnt + j] < 0.000001)
				{
					curCitiesCode.citiesCode = get2InverseSerize(i,j, sol.citiesCode, disMat);
					curCitiesCode.pathLength = getPathLength(curCitiesCode.citiesCode);
					cnt = 0;
				}
			}
		}
	}*/
}

//两点置首算子
solution operator2header(solution& sol, double* disMat)
{
	int citiesCnt = sol.citiesCode.size();
	double* tmp = new double[citiesCnt * citiesCnt];

	for(int i = 0; i < citiesCnt - 1; i++)
	{
		for(int j = i + 1; j < citiesCnt; j++)
		{
			tmp[i * citiesCnt + j] = getPathReduceCost(sol.citiesCode,get2InverseSerize(i,j, sol.citiesCode, disMat), disMat);
		}
	}

	int len = citiesCnt * citiesCnt - 1;
	int index = distance(tmp, max_element(tmp, tmp + len));
	vector<int> curBestSerize = get2InverseSerize(index / citiesCnt,index % citiesCnt, sol.citiesCode, disMat);
	solution curBestSol = {curBestSerize, getPathLength(disMat, curBestSerize)};
	delete[] tmp; tmp = NULL;
	return curBestSol;
}

//序列反转路径节约值
double getPathReduceCost(vector<int> oldCitiesCode, vector<int> newCitiesCode, double* disMat)
{
	return getPathLength(disMat, oldCitiesCode) - getPathLength(disMat, newCitiesCode);
}
//两点反转后的更新路径
vector<int> get2InverseSerize(int pt1,int pt2, vector<int> citiesCode, double* disMat)
{
	//重构路径
	int max = pt1 > pt2 ? pt1 : pt2;
	int min = pt1 < pt2 ? pt1 : pt2;
	vector<int> curCitiesCode;
	for(int i = 0; i <= min; i++)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	for(int i = max; i > min; i--)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	for(int i = max + 1; i < citiesCode.size(); i++)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	return curCitiesCode;
}

//得到两点置首后的新序列
vector<int> get2HeaderSerize(int pt1,int pt2, vector<int> citiesCode, double* disMat)
{
	vector<int> curCitiesCode;
	curCitiesCode.push_back(pt1);
	curCitiesCode.push_back(pt2);
	for(int i = pt1; i < pt2; i++)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	for(int i = 0; i < pt1; i++)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	for(int i = pt2; i < citiesCode.size() - 1; i++)
	{
		curCitiesCode.push_back(citiesCode[i]);
	}
	return curCitiesCode;
}

//剔除向量中重复序列,且保持原有序列的顺序
vector<int> delRepetitiveSequence(vector<int> oldSeq)
{
	vector<int> newSeq;
	vector<int>::iterator it1,it2;  
    for (it1 = oldSeq.begin(); it1 < oldSeq.end(); it1++)
    {
        it2 = find(oldSeq.begin(),it1,*it1);
        if (it2 == it1)
            newSeq.push_back(*it1);  
    }
	return newSeq;
}

//扰动函数--分块乱序重组函数
vector<int> shaking(solution inisol, int blockCnt)
{
	vector<int> noOrderCityCode;
	int* index = new int[blockCnt];
	//生成随机分块序列
	for(int i = 0; i < blockCnt; i++)
	{
		index[i] = i;
	}
	std::random_shuffle(index, index + blockCnt);
	int elementsCntPerBlock = inisol.citiesCode.size() / blockCnt;
	//分块
	vector<vector<int>> blockSeq;
	for(int i = 0; i < blockCnt; i++)
	{
		blockSeq.push_back(vector<int>(inisol.citiesCode.begin() + i * elementsCntPerBlock, 
			inisol.citiesCode.begin() + (i + 1) * elementsCntPerBlock));
	}

	//按照生成的随机序进行重组
	for(int i = 0; i < blockCnt; i++)
	{
		for(int j = 0; j < elementsCntPerBlock; j++)
		{
			noOrderCityCode.push_back(blockSeq[index[i]][j]);
		}
	}
	delete[] index; index = NULL;
	return delRepetitiveSequence(noOrderCityCode);
}

（3）主程序main.cpp

#include "vns.h"
#include "ctime"

int main()
{
	srand((unsigned) time(0));
	vector<point> pt;
	int cityCnt = getCitiesCoor("cities.txt", pt);
	cout << "此次共" << cityCnt << "个城市参与计算" << endl;
	//生成城市序列
	double* distanceMat = getDistanceMat(pt);
	//生成初始城市序列
	solution iniSol = generateIniSol(cityCnt, distanceMat);
	cout << "-------------初始路径----------------" << endl;
	outputSol(iniSol);
	solution bestSol = variableNeighborhoodSearch(iniSol, distanceMat);
	cout << "-------------最优路径----------------" << endl;;
	outputSol(bestSol);
	//输出结果
	FILE* output = fopen("resault.txt", "a+");
	fprintf(output, "\n路径序列：\n");
    for (int i = 0; i < cityCnt; i++)
    {
		fprintf(output, "%d, ", bestSol.citiesCode[i]);
    }
	fprintf(output, "\nlength = %lg\n", bestSol.pathLength);
	fclose(output);

	//资源清理
	delete[]distanceMat; distanceMat = NULL;
	return 0;
}

---

程序结果展示

---

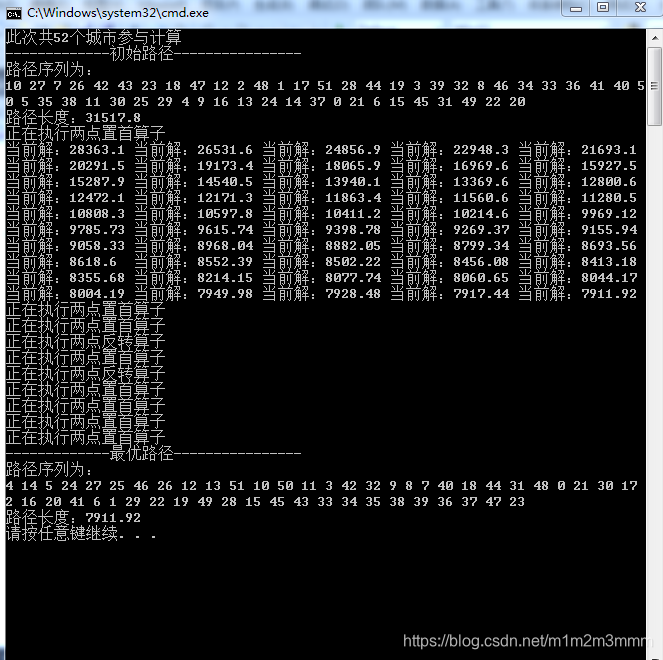
本文算例测试数据及路径可视化程序见博文：

https://blog.youkuaiyun.com/m1m2m3mmm/article/details/86558642

---

程序代码存在缺陷

（1）运行时间较长，不能满足大规模数据测试需求；（2）代码存在一定程度的冗余，算法搜索效果稳定性不强，寻优能力有待改善；（3）算子的效用体现不够明显，算法只能执行其中的某一个算子，便不会再更新更优解；但作为入门级程序，欢迎新手参考学习，也欢迎各位高手提出进一步优化建议。