图相关文章：
1. 图的建立 - 邻接矩阵与邻接表
https://blog.youkuaiyun.com/m15253053181/article/details/127552328?spm=1001.2014.3001.55012. 图的遍历 - DFS与BFShttps://blog.youkuaiyun.com/m15253053181/article/details/127558368?spm=1001.2014.3001.55013. 顶点度的计算https://blog.youkuaiyun.com/m15253053181/article/details/127558599?spm=1001.2014.3001.55014. 最小生成树 - Prim与Kruskalhttps://blog.youkuaiyun.com/m15253053181/article/details/127589852?spm=1001.2014.3001.55015. 单源最短路径 - Dijkstra与Bellman-Fordhttps://blog.youkuaiyun.com/m15253053181/article/details/127630356?spm=1001.2014.3001.55016. 多源最短路径 - Floydhttps://blog.youkuaiyun.com/m15253053181/article/details/128039852?spm=1001.2014.3001.55017. 拓扑排序AOV网https://blog.youkuaiyun.com/m15253053181/article/details/128042358?spm=1001.2014.3001.5501
目录
1 最小生成树问题
求解思想：
最小生成树问题的解决方案是基于贪心的思想，向空边集A中不断加入“合适”的边，使其扩展至一棵最小生成树
1.1 问题概述
现在我们需要修建道路来连通各个城市，已知各道路修建费用不同，那么如何确定修建方案，使得连通各个城市的成本最小？
将其转化为图论问题，即求权重最小的连通生成子图，这便是我们所说的最小生成树问题。
生成树的概念（图论）：
图T'=<V', E'>是无向图G的一个生成子图，并且是连通且无环的（树）。
显然，图的最小生成树并不唯一。
1.2 求解问题的思想
首先将问题抽象出来，以不同的线段和颜色来区分不同的顶点和边。
一个很自然的想法便是，任给一个空的边集A，不断向A中增加新边，则A会逐步扩展膨胀至一棵最小生成树。
因此，现在问题变转变为了如何寻找这样的边，使得其一定会扩展成最小生成树？
根据最小生成树的定义，显然，新边需满足以下两点要求：
① 需保证加入新边后，A仍是一个无环图；
② 需保证加入新边后，A仍是最小生成树的子集。
至此，问题再度转化。无环图我们暂且不说，如何保证A仍是最小生成树的子集呢？
此处需要一些图论的基础知识，简单给出两个概念。
给出以下定理：
如果边集A在割(S, V - S)中的某一侧，且(u, v)是横跨该割的所有边中最短的那条，则(u, v)便是我们要找的“新边”。
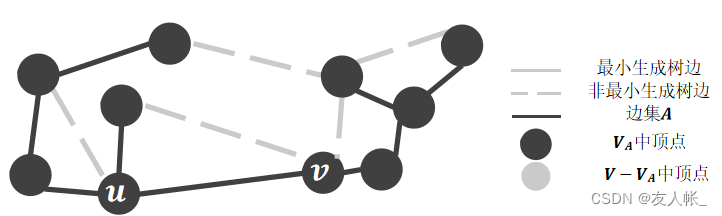
以上述图片为例来阐述这个定理，假设绿线左侧黑色的顶点构成了顶点集S，右侧灰色的顶点构成了顶点集V-S；左侧灰色实线表示确实是最小生成树的边，虚线表示不是最小生成树的边；右侧（V-S）的灰线，不论虚实，我们目前并不知道哪些是最小生成树的边。我们现在要做的就是找到所谓的“新边”，加入到左侧。
需要注意的有两点：
① “边集A在割(S, V - S)中的某一侧”的含义：以此图为例，边集A就是左侧灰色实线，他们全都在割的S这一侧，并不会有边存在于横跨的位置或者右侧V-S的部分。
② 这个定理是个动态的过程。（A初始为空集），当加入“新边”后，边集A扩展，同时将扩展到的新的顶点加入到割的某一侧（即S或V-S也是在不断更新的）。以此图为例，三条绿边为横跨，其中绿色实线为横跨中最短的那条，那么就将横跨纳入边集A，将与横跨相连的属于V-S中的那个顶点拉到V中，即边集A、顶点集V、V-S都进行了更新。
上述这段话可能略显抽象，拿上述图示自己画一下就很好理解了。
可以看到，最小生成树问题的求解是基于贪心的思想的，具体体现在每次加入的新边都是“横跨该割的所有边中最短的那条”。
那么如何具体来实现判断无环图与新边，便是以下两种算法要做的事情。
2 算法求解
2.1 Prim算法
（1）算法思想
第1步：任意选择一个顶点，作为生成树的起始顶点；
第2步：保持边集A始终为一棵树，选择割(V_A, V - V_A)；
第3步：选择横跨割(V_A, V - V_A)的边中最短的那条，加入到边集A中；
第4步：重复第2步与第3步，直至覆盖所有顶点。
其中，第2步始终为一棵树，便保证了无环。
（2）实现
由于邻接表的存储方式寻找相邻顶点较容易，所以用邻接表实现。
在具体实现的过程中，我们需要一些辅助数组：
| 辅助数组 | 作用 |
|---|---|
| visited[i] | 用于标记顶点i是否已入树，是为1，否为0 |
| dist[i] | 用于记录未入树的顶点与正在扩张中的子树A的最短距离；一旦该顶点入树，dist[i]不再修改，为最小生成树中边的权重 |
| pred[i] | 记录顶点i在最小生成树中的前驱是谁 |
下面以一个动图来实际看一下实现过程。（color为B(black)表示加入树，为W(white)表示未加入，灰色的点代表可以选择的点）：
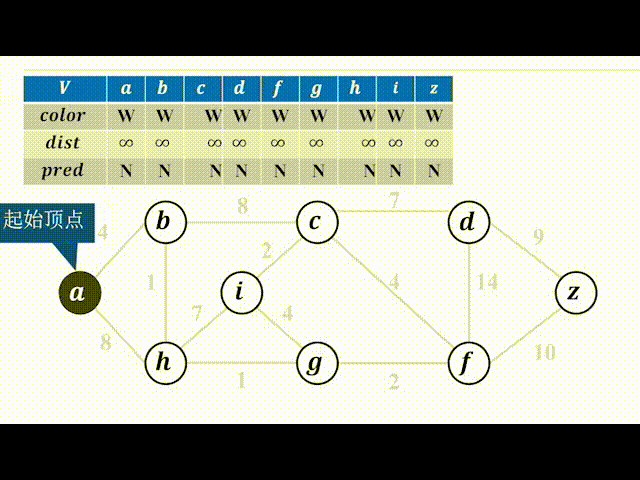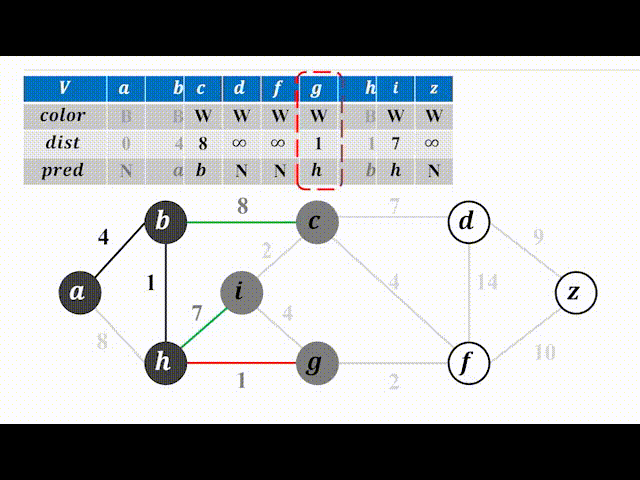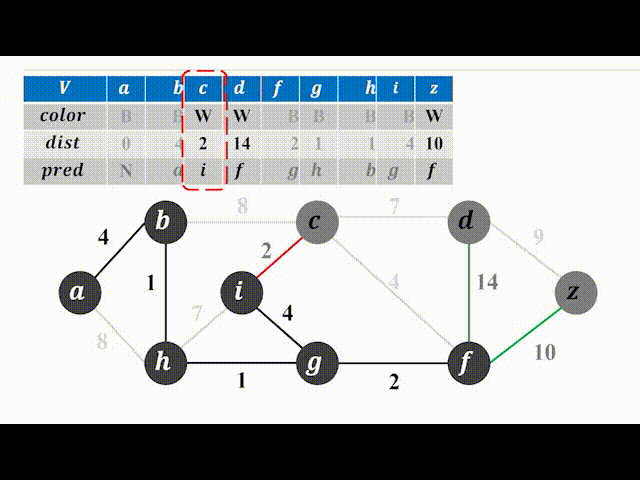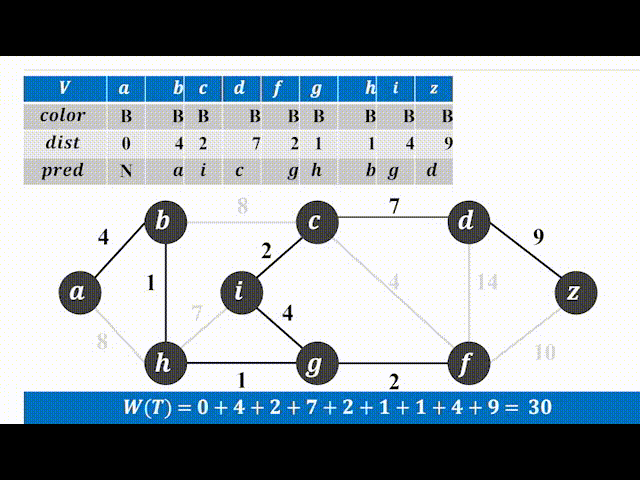
代码注释比较详细，不过多赘述，有以下几点需要注意：
① 需要牢牢记住dist[i]的含义；
② 请代入一个实例自己走一遍代码流程，不然比较抽象。
运行示例：
/* Prim */
void Prim(AdjList L)
{
int i, j;
int minDist; // 记录最小权值
int rec; // 记录新边的端点
LGNode pMove = NULL;
int *visited = (int *)malloc(sizeof(int) * L->numV); // 标记已入树
int *dist = (int *)malloc(sizeof(int) * L->numV); // 记录未入树的结点与子树A的距离
int *pred = (int *)malloc(sizeof(int) * L->numV); // 记录顶点前驱
int expense = 0; // 记录总花费
// 初始化
for (i = 0; i < L->numV; i++)
{
visited[i] = 0;
dist[i] = INF;
pred[i] = -1;
}
dist[0] = 0; // 选择第一个顶点作为起点（任选一个）
// Prim算法
for (i = 0; i < L->numV; i++) // 添加|V|次顶点
{
minDist = INF;
// 选出新边
for (j = 0; j < L->numV; j++) // 遍历dist数组，找出最小的那条边的端点（未访问过的）
{
if (!visited[j] && dist[j] < minDist)
{
minDist = dist[j];
rec = j; // 记录新边端点
}
}
// 引入了新边，故未入树的结点（实际上是与新边端点相邻的那些顶点）与子树A的距离可能会发生改变，更新dist
pMove = L->list[rec].next;
while (pMove) // 遍历新边端点的邻接顶点
{
if (!visited[pMove->v]) // 对于未访问过的那些顶点
{
if (pMove->dis < dist[pMove->v]) // 如果其到新边端点的距离小于其本身与子树A的距离，则更新
{
dist[pMove->v] = pMove->dis;
pred[pMove->v] = rec; // 将该顶点的前驱更新为新边端点
}
}
pMove = pMove->next;
}
visited[rec] = 1; // 新边标记为已入树
}
printf("Vertex num: \t");
for (i = 0; i < L->numV; i++)
{
printf("%2d ", i);
}
printf("\n");
printf("Vertex name: \t");
for (i = 0; i < L->numV; i++)
{
printf("%2c ", L->nameV[i]);
}
printf("\n");
printf("Vertex weight: \t");
for (i = 0; i < L->numV; i++)
{
printf("%2d ", dist[i]);
}
printf("\n");
printf("Vertex pred: \t");
for (i = 0; i < L->numV; i++)
{
printf("%2d ", pred[i]);
}
printf("\n");
}（3）算法分析
时间复杂度：O(V²)
在选出新边的过程中，我们需要对每个顶点都去遍历一遍，造成了内部循环的复杂度也是O(V)，那么如何进一步优化呢？
既然每次都是选择最短的边，我们很自然地想到可以用最小堆（优先队列）来实现，而最小堆的插入、取值、更新操作的时间复杂度都是O(logn)。
如果使用最小堆的结构来实现寻找新边的过程，可以把时间复杂度降到O(|E|log|V|)，实现优化。
程序的整体框架并不需要改变，请读者自行实现。
2.2 Kruskal算法
（1）算法思想
Kruskal算法采用最朴素的思想，既然需要保证加入新边后，A仍是一个无环图，那么就在选边的时候避免成环；需保证加入新边后，A仍是最小生成树的子集，则在每次选择时选择当前权重最小的边。
首先我们将每个顶点视作一个连通分量，接着按照边长升序序列，依次选择当前最短的边加入连通分量，若发现要加入的边的两个顶点在同一棵树上，则会构成环，便略过此边。重复这种操作，直至所有的边都被尝试过了，就得到了最小生成树。
具体操作流程可以归纳如下：
第1步：选取最小的边，构成一棵树；
第2步：在剩余的边中选取次小的边，若构成环，则选择再次小的边尝试；
第3步：重复第2步，直至覆盖所有点。
显然，在不断选取最小边的时候，会生成不止一棵树，森林不断地合并子树，最终形成一棵最小生成树。其中，每次选取不成环的最小边，是一种贪心策略。
我们先来直观地感受一下Kruskal算法：
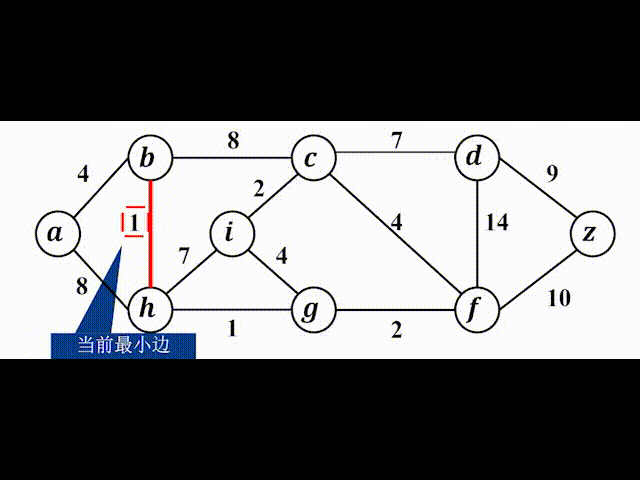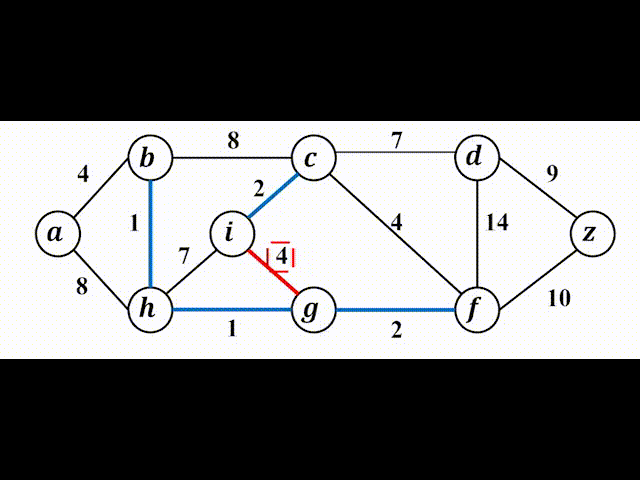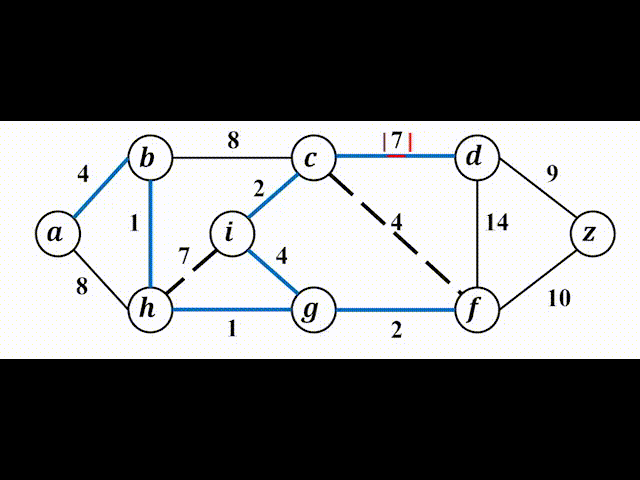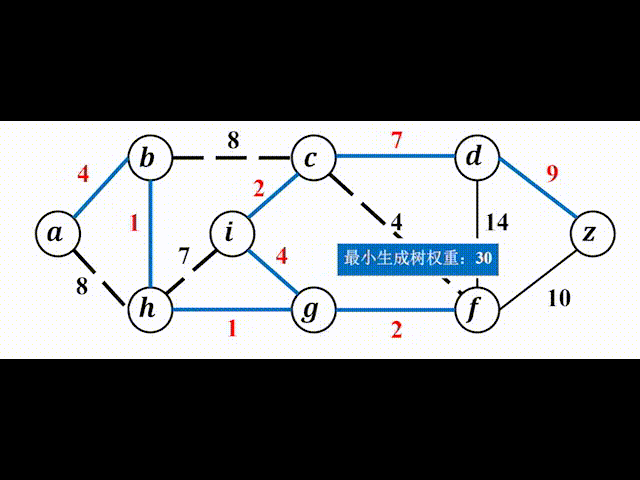
（2）并查集
我们只需要先对边按照权重升序排列，便可以保证每次选取的都是当前剩余的最短边。那么问题主要集中在：如何高效判定和维护所选边的顶点是否在一棵子树？
此处我们便需要使用到一种高级数据结构——并查集。
推荐一篇优秀博客，已经讲解足够清楚：并查集谦小白的博客-优快云博客并查集
这里我们采用如下结构的并查集：
给出并查集的操作：
/* 并查集数据结构 */
typedef struct union_find_set
{
int *nums; // 编号
int *parent; // 父结点
int *height; // 树高
} * UFS;
/*------------------------ 并查集的操作 ------------------------*/
/* 初始化并查集 */
UFS initUFS(int numV)
{
int i;
UFS set = (UFS)malloc(sizeof(struct union_find_set));
set->nums = (int *)malloc(sizeof(int) * numV);
set->parent = (int *)malloc(sizeof(int) * numV);
set->height = (int *)malloc(sizeof(int) * numV);
for (i = 0; i < numV; i++)
{
set->nums[i] = i;
set->parent[i] = i; // 父结点指向自己
set->height[i] = 1; // 每个结点都是高为1的树
}
return set;
}
/* 找根节点 */
int findRoot(UFS set, int node)
{
int root = node;
while (set->parent[root] != root) // 回溯往上找
{
root = set->parent[root];
}
return root;
}
/* 判断是否在同一棵树 */
int inSameset(UFS set, int node1, int node2)
{
int root1 = findRoot(set, node1);
int root2 = findRoot(set, node2);
return root1 == root2;
}
/* 合并两棵树 */
void unionSet(UFS set, int node1, int node2)
{
int root1 = findRoot(set, node1);
int root2 = findRoot(set, node2);
if (set->height[root1] <= set->height[root2])
{
if (set->height[root1] == set->height[root2])
{
set->height[root2]++;
}
set->parent[root1] = root2;
}
else
{
set->parent[root2] = root1;
}
}（3）实现
由于首先需要对边进行排序，这里使用邻接矩阵的存储方式会更容易一些。
运行示例：
鉴于整体代码较长，先给出核心代码：
// Kruskal
count = 0;
for (i = 0; i < G->numE; i++)
{
if (!inSameset(set, edge[0][i], edge[1][i])) // 两个顶点不在同一棵树中
{
// 将边加入到正在扩张的最小生成树中
MST[0][count] = edge[0][i];
MST[1][count] = edge[1][i];
MST[2][count] = edge[2][i];
unionSet(set, edge[0][i], edge[1][i]); // 合并不相交集
expense += edge[2][i]; // 记录总长
count++;
}
}完整代码：
void Kruskal(MGraph G)
{
int i, j, temp1, temp2, temp3;
int count = 0; // 记录边数
int edge[3][MaxVertexNum]; // 顶点1 顶点2 边长
int MST[3][MaxVertexNum]; // 最小生成树
UFS set = initUFS(G->numV);
int expense = 0;
// 读入所有的边
for (i = 0; i < G->numV; i++)
{
for (j = 0; j < i; j++)
{
if (G->dis[i][j] != -1)
{
edge[0][count] = i;
edge[1][count] = j;
edge[2][count] = G->dis[i][j];
count++;
}
}
}
// 对边进行排序 - 冒泡
for (i = 0; i < count; i++)
{
for (j = i; j < count; j++)
{
if (edge[2][i] > edge[2][j])
{
temp1 = edge[0][i];
temp2 = edge[1][i];
temp3 = edge[2][i];
edge[0][i] = edge[0][j];
edge[1][i] = edge[1][j];
edge[2][i] = edge[2][j];
edge[0][j] = temp1;
edge[1][j] = temp2;
edge[2][j] = temp3;
}
}
}
// Kruskal
count = 0;
for (i = 0; i < G->numE; i++)
{
if (!inSameset(set, edge[0][i], edge[1][i])) // 两个顶点不在同一棵树中
{
MST[0][count] = edge[0][i];
MST[1][count] = edge[1][i];
MST[2][count] = edge[2][i];
unionSet(set, edge[0][i], edge[1][i]); // 合并不相交集
expense += edge[2][i]; // 记录总长
count++;
}
}
printf("Vertex 1: \t");
for (i = 0; i < count; i++)
printf("%2d ", MST[0][i]);
printf("\n");
printf("Vertex 2: \t");
for (i = 0; i < count; i++)
printf("%2d ", MST[1][i]);
printf("\n");
printf("Distance: \t");
for (i = 0; i < count; i++)
printf("%2d ", MST[2][i]);
printf("\n\n");
}（4）算法分析
时间复杂度：𝑶(|𝑬|𝐥𝐨𝐠|𝑽|)
扫一扫
6586
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
