合法出栈顺序 —— 卡特兰数

当我们按一定顺序输入元素进栈时，往往会有多种序列；1，2，5，14，42······，我们发现，这与卡特兰数极为相似，那么何为卡特兰数？

它是组合数学中的一种常见数列，我们可以将它转化为几何问题，先对它有一个具体的认识：

在n*n的网格上，每次只能向右或向上走一格，在不穿越网格主对角线的情况下，从左下角（0,0）走到右上角（n，n）的不同路径计数,如图。

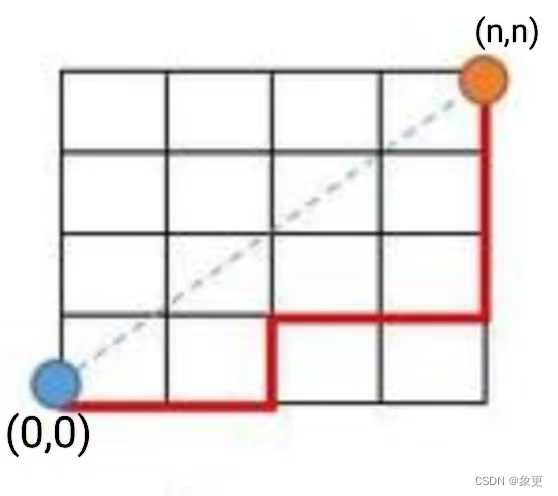
若不考虑穿越主对角线的情况，可以考虑为 

那么从(0,0)点到(n,n)点的过程中，我们总共需要向右移动n步，向上移动n步，一共2n步。我们可以理解为在2n步里面选出n步来向上移动，那么剩下的n步就是向右移动的步数，那么方案总数就是C (n,2n)；若考虑穿越主对角线的情况，如图，

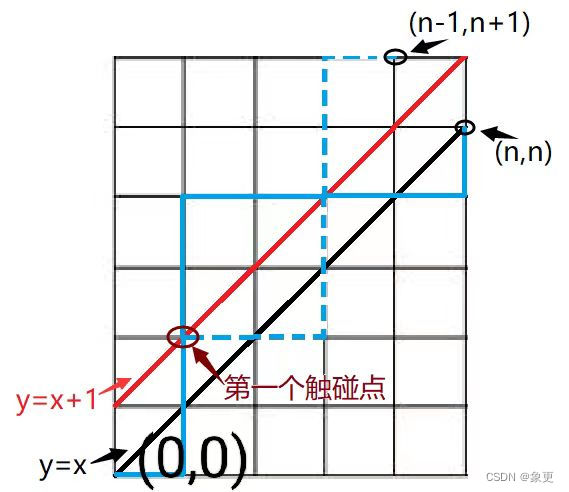
凡超越主对角线都可视为触碰到y=x+1,在第一个触碰点处，关于y=x+1对称，我们会发现所有触碰到y=x+1的路径都会对称到（n-1，n+1）处，共C(n-1,n+1)种，

我们可以得出Catalan(卡特兰数)=C (n,2n)-C(n-1,n+1);

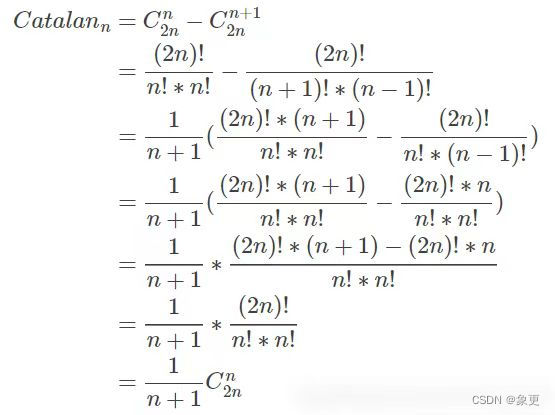
另Catalan(卡特兰数)=C (n,2n)-C(n-1,n+1)=f(0)f(n-1)+f(1)f(n-2)+······+f(n-1)f(0);

出栈元素顺序种类公式：

                                                  

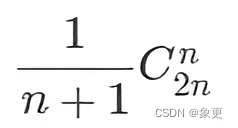
出栈顺序也可以用二叉排序树进行查找，感兴趣可以试着做一下！