从【拼车】问题的解法，简单介绍差分数组

 引入：

        力扣上第1094题，【拼车】

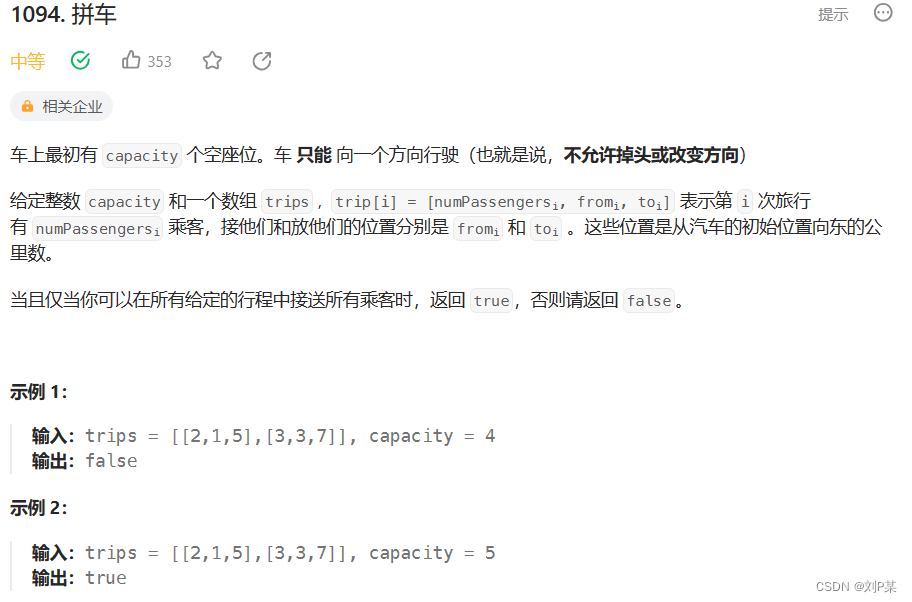        当时解这道题初步的想法是定义一个数组，下标表示里程数即车当前的位置，元素表示在这个时间点上，车内的乘客总人数。

因为车的位置是[0~1000]        所以，定义的数组的下标范围也就是0到1000

例如示例1：

        在第1公里的时候，上两个人，在第5公里的时候下车，所以对数组下标为[1~4]的区间内的元素每一个都加上2

        在第3公里的时候，上三个人，在第7公里的时候下车，所以对数组下标为[3~6]的区间内的元素每一个都加上3

对这个数组的操作就是

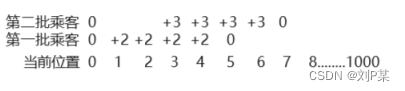
这样一个数组的结果就是：

0     2    2    5    5    3    3    0    0    0........0

可以看到这个数组的最大值是5，也就表示这辆车上最多的时候有5个人

只要判断这样一个数组的最大值，有没有超过车上座位的数量就可以了

        但是这就带来了一个问题：区间越大，需要操作的次数就越多

        如果一个人从第1公里坐到了第999公里，另外一个人从第2公里坐到了第1000公里，需要对数组中这两个区间的元素操作的次数就会大大增加。夸张点讲，试想如果这辆车行驶的总里程数是一万公里，或者十万公里呢？

        这个时候，传统的遍历修改方法显然是不太适合的，那么有没有什么方法，能够不用进行这么多次的操作，就侧面反映出数组某个区间的整体变化情况呢？

        此时就可以使用差分数组

差分数组定义：

        第一项与原数组相同，之后的每一项都等于原数组的这一项与前一项之差；

例如： 

原数组为 5 4 7 2 4 3 1

对应的差分数组为 5  (4-5)  (7-4)  (2-7)  (4-2)  (3-4)  (1-3)

                         即 5     -1      3        -5       2        -1      -2

性质一：

差分数组有一个重要的性质：对差分数组求前缀和数组，等于原数组

什么是前缀和数组？

 前缀和的定义很简单，就是数组这个位置之前的所有元素之和

还是拿上面的差分数组举例：

原数组：5 4 7 2 4 3 1

差分数组为：5     -1                   3                       -5       2        -1      -2

求前缀和为：5      4 (5+(-1))      7 (5+(-1)+3)       2        4        3        1

不难看出，前缀和数组就是原数组，求差分和求前缀这两个操作其实可以看成互逆操作。

那么差分数组是如何从侧面反映出原数组的区间整体变化情况的呢？

性质二：

        如果对原数组的某一个区间进行整体的增减，那么对应的差分数组只有区间首，以及区间尾的下一个位置会发生改变。

        例如：要对上面的数组的[1~4]进行整体+2
原数组就变为：5 6 9 4 6 3 1

           原差分数组：5     -1      3      -5      2       -1    -2
差分数组此时变为：5   (6-5) (9-6) (4-9) (6-4) (3-6) (1-3)
                         即：5      1      3       -5      2       -3    -2

                                        +2                                -2

此时发现，只有差分数组的[1] 和[5]发生了改变，[1]加上了改变量，[5]减去了改变量。

        由此性质可以反推，当差分数组的[ i ]+a，[ j+1 ]-a，此时求其前缀和数组，还原出来的原数组，在[ i~j ] 的区间上整体加上了a。

        当[i~j]这个区间非常大时，如果对原数组一个一个操作，将非常耗时。而用差分数组的性质反操作原数组，只需要进行两步操作，大大节约了时间，将区间操作转化为了节点操作。

 具体代码：

bool carPooling(int** trips, int tripsSize, int* tripsColSize, int capacity) {
    *tripsColSize = 3;
    int tomax = trips[0][2];    //找到最后一个下车的位置，申请空间的时候就不需要从0~1000
    for(int i=1;i<tripsSize;i++)
    {
       if(tomax<trips[i][2])
       tomax = trips[i][2];
    }

    int* diff = (int*)malloc(sizeof(int)*(tomax+1));
    memset(diff,0,sizeof(int)*(tomax+1));  //数组初始化

    for(int i=0;i<tripsSize;i++)
    {
        diff[trips[i][1]] += trips[i][0];  //上车位置加上乘客改变量
        diff[trips[i][2]] -= trips[i][0];  //下车位置减去乘客改变量
        if(diff[trips[i][1]]>capacity)     //假如加完以后发现已经大于最大座位数
        return false;                   //直接返回false
    }

    int count = 0;
    for(int i=0;i<tomax;i++)
    {
        count += diff[i];        //还原原数组，直接找到最大值
        if(count>capacity)
        return false;
    }
    free(diff);
    return true;
}

 总结：

        差分数组主要的适用场景是对原始数组进行频繁的区间增减操作，这个时候使用差分数组能够快速的完成，同时能够快速获得更新后的数组各个位置的值。

        主要就是把区间遍历操作，变为了对两个节点进行操作，再根据性质转换成原数组。