笔试编程算法题（五）（C++代码）

已于 2025-03-05 21:53:48 修改
阅读量860 收藏 18
点赞数 19
分类专栏： 错题复习 文章标签： 算法 c++ 开发语言
于 2024-12-18 22:44:27 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_74099572/article/details/143711861
版权

1.最长有效括号

解法：动态规划

状态表示：dp[i]表示，以i位置为结尾的，最长的有效括号长度。

状态转移方程：
这里就需要进行分情况讨论了。

1.当s[i] == '('时：

此时的s[i - 1]又分为两种情况：

a.当s[i - 1] == ')'时：此时这两个字符就是 ... )(...，显然这已经不可能拼接成一个有效的括号了，所以此时dp[i] = 0。

b.当s[i - 1] == '('时：此时两个字符就是 ...((...，然而这种情况下 它俩是有可能拼接成为一个有效括号的，并且在s[i - 1]前面有可能已经存在了有效括号，因此 dp[i] = dp[i - 1]。

2.当 s[i] == ')'时：

此时s[i - 1]同样分为两种情况：

a.当s[i - 1] == '('时：此时两个字符 ...()...，它俩刚好可以组成一个有效括号，并且dp[i - 1]之前也可能存在有效括号，因此此时dp[i] = dp[i - 2] + 2

b.当s[i - 1] == ')'时：此时这两个字符 ...))...，此时还不能判断它俩是否在一个有效括号内，比如它俩的前两个字符是 ((，因此还需要需要再判断一下，s[i - 1 - dp[i - 1] 是否 == '('，如果等于，那么此时dp[i] = dp[i - 1] + 2。

但是这里还有一种很容易被忽略的情况，

比如示例： ()(())，我们发现在 (())之前还有一个有效括号，不能把它给漏了，因此此时：
dp[i] = dp[i - 1] + 2 + dp[i - 2 - dp[i - 1]]，这里看着比较绕，但是用图就比较好理解了：

 初始化和边界情况：
dp表中表示的是长度，所以默认为0即可。

关于边界这里，因为会用到i - 2的值，所以不加以处理的话就会越界，这里有一个技巧，对于字符串，我们可以让 s = "  " + s。也就是给s前面加了两个辅助空间，但是又不影响计算。

关于返回值：
因为我们要求的是最大长度，而dp[i]表示的是以i位置为结尾的，不一定是最大值，因此我们要返回整个dp表中的最大值。

代码：
 

class Solution {
public:
    int longestValidParentheses(string s) {
        s = "  " + s; // 方便处理边界情况，以及下标映射
        int n = s.size();
        vector<int> dp(n);
        int ret = 0;
        for(int i = 2; i < n; ++i)
        {
            if(s[i] == ')')
            {
                if(s[i - 1] == '(') dp[i] = dp[i - 2] + 2;
                else
                {
                    if(s[i - 1 - dp[i - 1]] == '(') 
                    {
                        // 这里才符合一个有效子串
                        dp[i] += dp[i - 1] + 2;
                        dp[i] += dp[i - dp[i - 1] - 2];
                    }                 
                }
            }
            else 
            {   // 这里也要区分能不能拼接成有效子串
                if(s[i - 1] == '(') dp[i] = dp[i - 1];
            }
            
            ret = max(ret,dp[i]);
        }

        return ret;
    }
};

2.最长公共子序列 

 

解法：动态规划 

本题可是是该类问题的母版题。

状态表示：dp[i][j] 表示 s1 在区间[0,1]和 s2 在区间 [0,j] 它们最长的公共子序列的长度。

状态转移方程：
1.当s1[i] == s2[j]：dp[i][j] = dp[i - 1][j - 1] + 1

2.s1[i] != s2[j] ：

此时又分为三种情况：

a.dp[i - 1][j] 

b.dp[i][j - 1]

c.dp[i - 1][j - 1]。

我们只要到这三个范围中找到最大值即可。

但是有一个细节，那就是dp[i - 1][j] 和 dp[i][j - 1]其实已经包含dp[i - 1][j - 1]了，所以只需要考虑这两种情况就可以了。

初始化：
因为会用到i - 1 和 j - 1，所以可以多开一行和多开一列来处理边界问题。

并且在字符串这里，我们可以给原始字符串头插一个辅助结点的方式，来方便后续进行下标映射。

dp表中的元素默认都为0即可。

代码：
 

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int n = text1.size();
        int m = text2.size();
        text1 = " " + text1;
        text2 = " " + text2;
        vector<vector<int>> dp(n + 1,vector<int>(m + 1));

        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <= m; ++j)
            {
                if(text1[i] == text2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i - 1][j],dp[i][j - 1]);
            }
        }

        return dp[n][m];
    }
};

3.编辑距离 

解法：动态规划

状态表示：
dp[i][j] 表示，s1 的[0,i] 转化到 s2 的[0,j]所需要的最小步数。

状态转移方程：

对于最后一个位置分为两种情况：
1.s1[i] == s2[j]，那么dp[i][j] = dp[i - 1][j - 1]。

2.s1[i] != s2[j]，那么此时又分为三种情况：

a.s1 删去一个字符，那么此时dp[i][j] = dp[i - 1][j]。

b.s1 新增一个字符 ，那么此时dp[i][j] = dp[i][j - 1]。

c.对s1[i]进行替换，使其等于s2[j]，那么此时dp[i][j] = dp[i - 1][j - 1]。

这三种情况取最小值，然后再 + 1即可。

初始化：
因为会用到 i - 1，j - 1，所以依旧可以多开一行和多开一列来防止越界问题。

还有一个容易忽略的点就是：
对于第一行和第一列：

比如第一行，也就是当s1为空时，此时我们要想转化为s2，只能新增，当s2为空时，s1只能删减

代码：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.size();
        int m = word2.size();
        vector<vector<int>> dp(n + 1,vector<int>(m + 1));
        word1 = " " + word1;
        word2 = " " + word2;
        for(int i = 0; i <= n; ++i) dp[i][0] = i; // 初始化
        for(int j = 0; j <= m; ++j) dp[0][j] = j;

        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <= m; ++j)
            {
                if(word1[i] == word2[j]) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = min(dp[i][j - 1],min(dp[i - 1][j - 1],dp[i - 1][j])) + 1;
            }
        }

        return dp[n][m];
    }
};

4.多数元素 

本题有三种解法：

这里简单介绍一下前两种：

1.用一个hash表来统计各元素出现的次数，返回出现次数最大的即可。

时间复杂度和空间复杂度都是 O(N)。

2.将数组进行排序，排完序后，数组的中间点一定就是众数。

时间复杂度为 O(N * logN)，空间复杂度为 O(1)。

这里说下第三种解法：
摩尔投票法：
 用一个ret变量来标记最终结果，用votes变量来记录当前众数ret的票数。

遍历nums数组：
当 x == ret时，票数 + 1；否则 票数 - 1

当当前票数减到0时，将ret更新为当前的元素x。

这里的解法其实跟动态规划的思想比较像，当某一个更好的状态出现之前，这一次的答案从之前最好的状态中获取。

代码：

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int votes = 0;
        int ret = nums[0];
        for(auto x : nums)
        {
            if(votes == 0) ret = x;
            if(ret == x) ++votes;
            else --votes;
        }

        return ret;
    }
};

另外本题保证了一定会有一个众数，如果没有这个保证，那么我们需要再进行一次遍历，看看我们选出来的这个众数出现的次数是否真的大于数组的 一半。

5.颜色分类 

 

解法流程：
首先看第一种常规解法，也就是基于快排的思想，选取一个基准值，将数组划分成三份。

在本题基准值就是1

代码：

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int n = nums.size();
        int left = -1,right = n;
        int i = 0;
        while(i < right)
        {
            if(nums[i] == 1) ++i;
            else if(nums[i] > 1) swap(nums[--right],nums[i]);
            else swap(nums[++left],nums[i++]);
        }
    }
};

还有一种巧妙的解法：
这个解法的思路：首先将数组所有的元素都设置为2，此时会存在一些被错误覆盖了的0和1，然后再将 x < 2的元素全部都设置为1，此时还存在一些被错误覆盖了的0，最后再将x < 1元素设置为0，此时所有的2，1，0都是正确的。

可以理解为这是一个刷油漆的过程：

一开始都是：22222222

然后就变成：11112222

最后会变成：00112222

代码：

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int n0 = 0,n1 = 0;
        for(auto& x : nums)
        {
            int tmp = x;
            x = 2; // 先直接置为2
            if(tmp < 2) nums[n1++] = 1; // 然后再置为1
            if(tmp < 1) nums[n0++] = 0; // 最后再置为0
        }
    }
};

6.下一个排列 

 

解法流程：

我们需要从后往前找到一个大数，然后在大数的前面再找到一个小数，让它们进行交换，然后再将大数后面的元素进行一个逆置即可。

要点：大数和小数之间要尽可能的紧凑，找到符合要求的大数和小数之后，它们在小数后面的元素都是降序的。 

解题步骤：

先将找到符合要求的数对(i,j)，找到后，说明此时的[j,end]是降序的（注意是闭区间），再从[j,end]这个区间中，从后往前找，直到找到一个元素k，使得nums[i] < nums[k]，那么此时就可以交换nums[i]和nums[k]的值，然后对于[j,end]区间进行一个逆置即可。

代码：

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size();
        for(int i = n - 2; i >= 0; --i)
        {
            if(nums[i] < nums[i + 1]) // 找到数对了
            {
                for(int j = n - 1; j >= i + 1; --j)
                {
                    if(nums[i] < nums[j]) 
                    {
                        swap(nums[i],nums[j]);
                        reverse(nums.begin() + i + 1,nums.end()); // 用逆置而不是sort
                        return;
                    }
                }
            }
        }
        return sort(nums.begin(),nums.end());
    }
};

这里关于逆置[j,end]的元素用reverse而不是用sort，是因为已经确定这个区间的元素是降序了，用sort会使用到额外的空间，所以使用reverse。

7.寻找重复数 

解法：双指针。

这道题的思路可以参考环形链表2那道题。

我们可以将数组想象成一个链表，比如示例1的数组：

这里形成链表的要点就是：将数组的下标 n 和nums[n]建立一个映射关系。

 如下：

到这里，我们就可以通过定义快慢双指针，用解决环形链表2的方式找到环的入口，也就是重复的数了。

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = 0,fast = 0;
        slow = nums[slow];
        fast = nums[nums[fast]];
        while(slow != fast)
        {
            slow = nums[slow];
            fast = nums[nums[fast]];
        }

        fast = 0;
        while(fast != slow)
        {
            slow = nums[slow];
            fast = nums[fast];
        }

        return fast;
    }
};

8.删除有序数组中的重复项 II 

 

解法：双指针。

其实解决这类问题是有通用解法的。

还有一道题是： 删除有序数组中的重复项

它的不同点只在于：数字只能出现一次。

而本题可以出现两次，对于这类题，我们假设它能出现的次数是k次。

那么对于这类问题：

对于某一个数字 i ，对于前k个数字相同，我们可以直接保留，对于后面的数字：与当前的位置进行比较，如果不相同才会保留。

于是定义两个双指针slow和fast 

比如序列：1111222

对于前两个1，我们会保留，但是从下标2开始，如果当前的数字仍然和 （2 - k）也就是0下标的数字相同的话，slow不会继续向前移动，fast则继续向前移动。

当slow移动到哪，说明数组的大小就是多少。

代码：

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int k = 2; // 要保留多少个数
        int n = nums.size();
        if(k >= n) return n; // 特殊情况
        int slow = k,fast = k;
        while(fast < n)
        {
            if(nums[fast] != nums[slow - k])
            {
                nums[slow] = nums[fast];
                ++slow;
            }
            ++fast;
        }

        return slow;
    }
};

9.O(1)时间插入、删除和获取 

 

题解：
题目的要求很简单，那就是要求 插入和删除，以及随机获取一个元素的时间复杂度为O(1)。

对于插入和删除，想要实现时间复杂度为O(1)，我们很容易就能想到哈希表。

但是对于以O(1)时间随机获取一个元素， 此时数组貌似才是最合适的选择。

但是我们该怎样将数组和哈希表搭配在一起呢？

这里最大的难点就在于：

在删除元素的时候，除了在哈希表中删除元素，我们该怎样将这个元素在数组中也以O(1)的时间复杂度删除呢？

思路：
数组v中存的就是元素的值。，对于哈希表hash中的映射关系是 数组索引 映射 值。

对于要被删除的元素，我们只要把它放置到数组的末尾即可。这样调用pop_back()删除的时间复杂度也是O(1)的。

同时记得也更改一下hash中，数组原来最后一个值的索引。

代码：

class RandomizedSet {
private:
    vector<int> v; // 存的值
    unordered_map<int,int> hash; // 值 映射 索引
    int index = -1; // 当前可以用到的下标最大值
public:
    RandomizedSet() {
        srand(time(0));
    }
    
    bool insert(int val) {
        if(hash.count(val) > 0)
        {
            return false;
        }
        else 
        {
            hash[val] = ++index;
            v.push_back(val);
            return true;
        }
    }
    
    bool remove(int val) {
        if(hash.count(val) > 0)
        {
            int i = hash[val];
            // 把需要在数组删除的元素放到数组末尾，这样使用pop_back的方式删除就是O(1)
            hash[v[index]] = i;
            swap(v[i],v[index]); 

            hash.erase(val);
            v.pop_back();
            --index;
            return true;
        }
        else 
        {
            return false;
        }
    }
    
    int getRandom() {
        int ret = rand() % (index + 1);
        return v[ret];
    }
};

10.加油站 

解法：

第一种：用图的思想来分析。

对于示例：
 

以该题为例：
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

可以画出这样一个图：

其中绿色柱状表示当前加油站能加多少油，橙色柱状表示移动到当前加油站需要花费多少油。

蓝色虚线表示：当前到达当前加油站对你当前油量的净值。

黑色实线表示：当前油量的总剩余量。

图中的起点是以索引0开始的，为了符合题意，黑色实线的值必须一直保持在X轴及以上，那么此时选择起点的关键点：

油量亏空最大的一步必须要放在最后一步走，这样可以尽可能的等待之前的油量救助。

代码：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        int spare = 0; // 当前的油量
        int min_spare = 0x3f3f3f3f; // 油量亏空的最大值
        int min_index = 0; // 油量亏空最大值的索引
        for(int i = 0; i < n; ++i)
        {
            spare += gas[i] - cost[i]; // 计算当前的油量
            if(spare < min_spare)
            {
                min_spare = spare;
                min_index = i;
            }
        }

        // 关键点：油量亏空最大的一步要放在最后一步走，因此要返回的不是min_index
        // 而是 min_index + 1
        // 如果油量小于0，说明不能走一周，那么返回-1
        return spare >= 0 ? (min_index + 1) % n : -1;
    }
};

 时间复杂度O(N)，空间复杂度O(1)。

第二种解法：贪心

我们先预处理一个数组，diff，先将当前加油站的净值计算出来。

还是以示例1为例：

贪心的地方就是：当我们遍历到一段正数净值区间的第一个值时，开始计算它是否能够绕一周。

这里的细节就是：

用step表示当前走了多少步，rest表示当前油量。如果setp还在走的时候，rest<0了，那么说明无法绕一周，那么此时的i += step（也就是直接跳过了刚刚遍历的区间），然后继续寻找下一个正数净值区间的第一个值。

代码：

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        vector<int> diff(n);
        for(int i = 0; i < n; ++i) diff[i] = gas[i] - cost[i]; // 预处理

        for(int i = 0; i < n; ++i)
        {
            if(diff[i] < 0) continue;

            int step = 0; // 移动的步数
            int rest = 0; // 当前油量
            for(;step < n; ++step)
            {
                int index = (step + i) % n;
                rest += diff[index];
                if(rest < 0) break;
            }    
            if(rest >= 0) return i;
            i += step;
        }

        return -1;
    }
};

时间复杂度O(N),空间复杂度O(N)。

11.分发糖果 

解法：贪心

对于糖果的分配，需要满足两个条件：
1.每个孩子至少要有一个糖果。这个规则容易理解也容易满足。

2.相邻的孩子评分更高的孩子会获得更多的糖果。

对于这个规则，我们可以对其进行拆分，假设现在有孩子A和孩子B，那么就存在三种情况：

1.孩子A评分大于孩子B，此时A的糖果就必须多余B，我们对这种情况称为“左规则”，因为本题需要求的是最少糖果数目，因此我们可以让A的糖果数比B只多1，这也是本题贪心的所在。

2.孩子B的评分大于A，对这种情况称为“右规则”，同理，我们让B的糖果数比A多1。

3.两个孩子的评分相同，那么我们让它俩的糖果数维持不变。

 本题需要考虑的重点就是，分配给孩子们的糖果数量必须要同时满足左规则和右规则。

算法流程：

我们可以定义两个数组left和right，它们都表示分配给对应下标孩子的糖果数，把它们默认的值初始化为1，先从左往右遍历数组，先计算出只满足左规则时，分配给对应下标孩子的糖果数是多少，也就是计算left数组；接着再从右往左遍历数组，计算只满足右规则时，分配给对应下标的孩子的糖果数是多少，也就是计算right数组。

最终，如果我们需要同时满足左规则和右规则的话，应该取二者的最大值。

最后，再考虑一下边界问题，对于计算左规则时，0号下标是计算不到的，因为它的左边是-1，也就是没有孩子；同理，对于计算右规则时，n - 1下标也是计算不到的。为了同时满足左规则和右规则，我们可以手动的把计算不到的值加上。

代码：

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n = ratings.size();
        vector<int> left(n,1);
        vector<int> right(n,1);
        int ret = 0;
        for(int i = 1; i < n; ++i)
        {
            if(ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
        }
        ret += left[n - 1]; // 因为n - 1这个位置只有左规则，无法计算右规则，所以提前加上
        for(int i = n - 2; i >= 0; --i)
        {
            if(ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
            ret += max(left[i],right[i]);
        }
        return ret;
    }
};

12.整数转罗马数字 

 

 

解法：
本题主要就是用哈希的思想来解决问题。

大致的思路很容易想到，但是将思想转化成简洁的代码还是有一点难度的，这里就直接看代码了

class Solution {
public:
    string intToRoman(int num) {
        int values[] = {1000,900,500,400,100,90,50,40,10,9,5,4,1}; // 共13对映射关系
        string reps[] = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
        string ret;
        for(int i = 0; i < 13; ++i)
        {
            while(num >= values[i])
            {
                ret += reps[i];
                num -= values[i];
            }
        }

        return ret;
    }
};

13.Z字形变换 

 

解法：
我们可以设置一个flag，flag初始值 = 1。再设置一个vetcor<string> tmp这样的字符串数组，可以用它的下标来映射这是第几行的字符串。

然后遍历字符串s，设它的每个元素是ch，i表示行号：
1. tmp[i] += ch
2.i += flag

3.当i到达转折点时(i == 0 || i == numRows - 1)时，flag = -flag

最后将字符串数组中的字符串相加即可。

代码：
 

class Solution {
public:
    string convert(string s, int numRows) {
        if(numRows < 2) return s; // 特殊情况
        vector<string> tmp(numRows);
        int i = 0;
        int flag = 1;
        for(auto ch : s)
        {
            tmp[i] += ch;
            i += flag;  
            if(i == 0 || i == numRows - 1)
            {
                flag = -flag;
            } 
        }
        
        string ret;
        for(auto& s : tmp) ret += s;

        return ret;
    }
};

14.串联所有单词的字串 

解法：滑动窗口

本题中 “words 中所有字符串 长度相同。” 这个条件很重要。

我们可以先将words中的单词放在一个哈希表中，并统计它们出现的次数。

我们的滑动窗口的大小的单位可以看作是words数组的大小，而不是字符串的个数。

关于每次滑动窗口移动的步长：就是words中每个元素的大小，也就是words[0].size()。

滑动窗口执行的次数：同样也是words中每个元素的大小，也就是words[0].size()。

代码：
 

class Solution {
public:
//滑动窗口
//使用两个hash表，一个用来存words中的元素作为参考标准
//另一个hash表存s中的元素，用来判断是否要增加有效字符串的个数
    vector<int> findSubstring(string s, vector<string>& words) {
        vector<int> v;
        int len=words[0].size(),m=words.size(),n=s.size();
        map<string,int> hash1;
        map<string,int> hash2;
        for(auto e:words) hash1[e]++;
        int count=0,sum=0;//count为有效字符串的数量，sum为当前字符串的数量
        //外层循环的次数为word中每个元素的长度
        for(int i=0;i<len;i++)
        {
            //每次内层循环完后记得要重置字符串的数量大小。
            sum=0;
            count=0;
             //每次循环记得要清空hash2
            hash2.clear();
            for(int left=i,right=i;right<n;right+=len)
            {
                sum++;
                string in=s.substr(right,len);
                //小优化：因为map[x]如果x不存在，会先插入x，再进行比较，这样效率低
                // 我们可以直接先判断x是否存在，存在再比较
                //hash1中，然后再比较。
                if (hash1.count(in) && hash2[in]++ < hash1[in])
                {
                    count++;
                }
                if(sum>m)//出窗口，并且判断删除的left是否为有效字符串
                {
                    string out=s.substr(left,len);
                    if(hash1.count(out)&&hash2[out]--<=hash1[out]) count--;
                    left+=len;
                    sum--;
                }
                if(count==m) v.push_back(left);//更新结果
            }
        }
        return v;
    }
};

15.生命游戏 

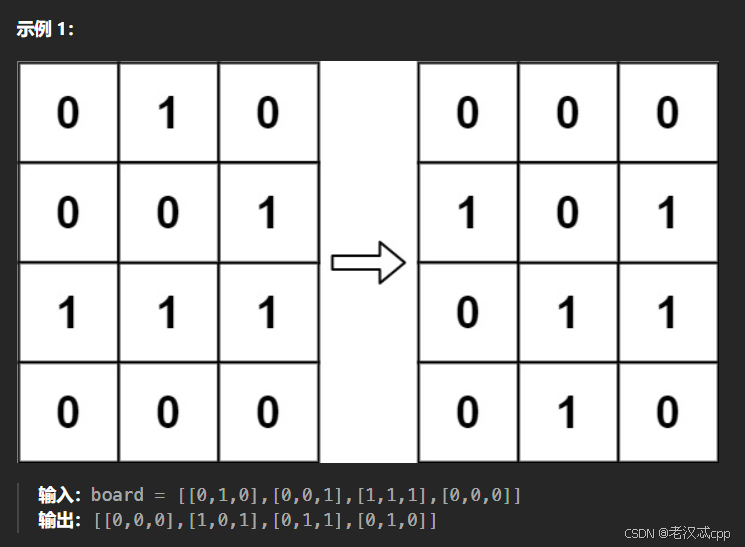
解法：

暴力解法很容易想到， 直接创建一个数组，这样空间复杂度为O(N * M)

优化就是，对于每一个board数组，每一个数据，我们可以用第二个保存结果，

最后将board数组的每一个数据都右移一位即可。

代码：
 

class Solution {
    int dx[8] = {0,0,1,1,1,-1,-1,-1};
    int dy[8] = {1,-1,0,1,-1,0,1,-1};

public:
    void gameOfLife(vector<vector<int>>& board) {
        int m = board.size(),n = board[0].size();
        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                int lives = 0;
                // 先计算八个方向有多少个活细胞
                for(int k = 0; k < 8; ++k)
                {
                    int x = i + dx[k];
                    int y = j + dy[k];
                    if(x >= 0 && x < m && y >= 0 && y < n && (board[x][y] & 1) == 1)
                    {
                        ++lives;
                    }
                }
                if((board[i][j] & 1) == 1)
                {
                    if(lives == 2 || lives == 3)
                    {
                        board[i][j] |= 2; // 将第二个比特位置为1
                    }
                    // 反之第二个比特位为0
                }
                else 
                {
                    if(lives == 3)
                    {
                        board[i][j] |= 2; // 同理
                    }
                }
            }     
        }  

        for(int i = 0; i < m; ++i)
        {
            for(int j = 0; j < n; ++j)
            {
                board[i][j] >>= 1; // 右移一位，第二个比特位上的结果覆盖到第一个比特位上
            }
        }  
    }
};

16.寻找峰值 

 

1.暴力解法：

 

此时一共分为三种和情况。（注意，题意中 nums[-1]和nums[n]是负无穷）

以最坏的情况3来看，事件复杂度为O(N)。

2.二分查找

 

对于一个位置i，分为两种情况，这两种情况都可以把数组分成两段，也就是具备二段性

对于情况1:

nums[i] > nums[i + 1] 那么仔细思考便可以推出 以i为划分的左半部分数组一定存在峰值，而右半部分可能存在。

情况2：

nums[i] < nums[i + 1]，同理，此时以i为划分的右半部分数组一定存在，而左半部分不一定。

至此根据二段性即可写出代码：

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        int left = 0,right = n - 1;
        while(left < right)
        {
            int mid = (right - left) / 2 + left;
            if(nums[mid] < nums[mid + 1]) left = mid + 1;
            else right = mid;
        }

        return left;
    }
};

  

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值