逻辑斯蒂回归

逻辑斯蒂回归

什么是逻辑斯蒂回归

其实就是解决二分类问题的一个算法，其中逻辑斯蒂是个函数这个函数是一个饱和函数（这类函数叫sigmoid），其值在0~1之间

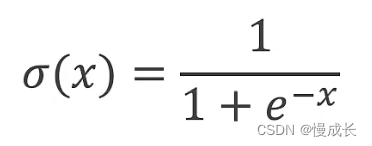
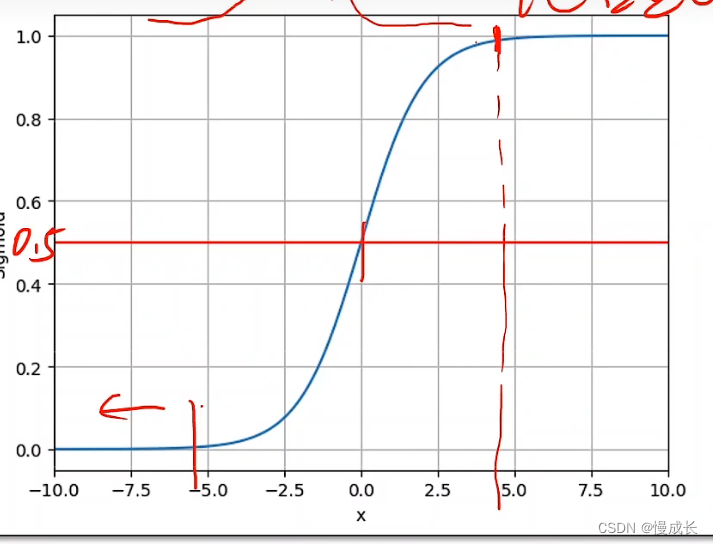
什么是二分类

二分类问题是机器学习和统计学中的一种常见问题类型，其中目标是将数据分为两个互斥的类别或类别标签。这两个类别通常分别被称为正类别（positive class）和负类别（negative class）

以下是一些常见的示例二分类问题：

1. 垃圾邮件检测：根据电子邮件的内容和特征，将每封电子邮件标记为垃圾邮件（正类别）或非垃圾邮件（负类别）。

2. 疾病诊断：根据医疗检查结果和患者的临床特征，将患者分类为患有某种疾病（正类别）或健康（负类别）。

3. 信用风险评估：根据申请人的信用历史、收入和其他相关信息，将信用卡申请者分类为高风险（正类别，可能违约）或低风险（负类别，不太可能违约）。

分类问题实际处理方式

不同于线性回归，分类问题不连续，分类问题解决方法是对于每个类计算与当前值匹配的概率，再用这个将类映射成概率的，可以很好满足建立方程完成概率的映射
实际计算上，就是实现输入值映射到预测值y，y为概率在0~1之间，这个映射关系大概如下，w、b则是要调配求出的系数，也就是需要求得的权重

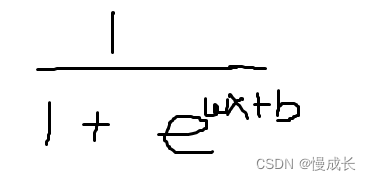
对于神经网络的单元来说，其处理分类问题就是吧wx+b看做一个整体，代入到函数，

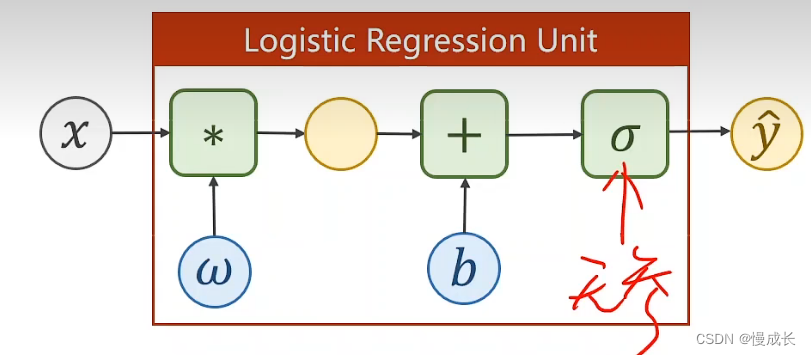
求损失值

因为不同于线性模型，这里是分布之间的差异，比如所给数据集p（class=1）= 0.5与p（class=0）= 0.5与预测值p_hat（class=1）= 0.6与p_hat（class=0）= 0.4之间的差距，这种用我们用交叉熵来计算，公式及解释：


所以对事件当为1时候和为0时候的概率求交叉熵得到损失函数：

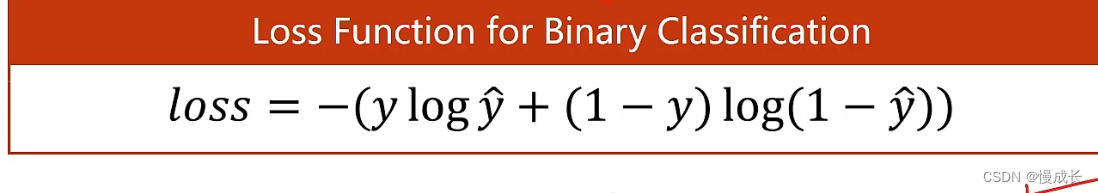
这个就是二分类所用的损失函数，叫
做BCE，以上是一条数据的损失，对应小批量数据的损失，则对BCE求和。

代码

import torch

# import torch.nn.functional as F

# prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])


# design model using class
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        # y_pred = F.sigmoid(self.linear(x))
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred


model = LogisticRegressionModel()

# construct loss and optimizer
# 默认情况下，loss会基于element平均，如果size_average=False的话，loss会被累加。
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# training cycle forward, backward, update
for epoch in range(1000):
    y_pred = model(x_data)
    loss = criterion(y_pred, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)