Hot100 —— 二叉树

二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

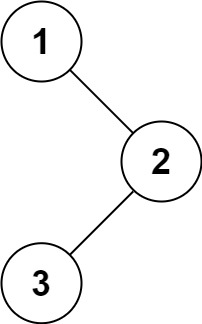
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

方法一：递归（最容易想到）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right


class Solution:

    def inorder(self, root: Optional[TreeNode], res: List[int]) -> None:
        if not root:
            return
        #中序遍历：左中右
        #很容易改成前序/后序遍历
        self.inorder(root.left, res)
        res.append(root.val)
        self.inorder(root.right, res)

    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        self.inorder(root, res)
        return res

方法二：颜色标记（模拟栈）

兼具栈迭代方法的高效，又像递归方法一样简洁易懂

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:

        #第一次访问到节点，置节点为白色
        #已访问到节点，把节点置为灰色
        #如果遇到的节点是白色，则将其置为灰色，并将其右子节点、自身、左子节点分别入栈
        #（因为是模拟栈先进后出，所以需要先让右子节点入栈）
        #如果遇到的节点是灰色，则将节点的值加到res中

        White, Grey = 0, 1
        res = []

        stk = [(White, root)]        
        while stk:
            color, node = stk.pop()
            if not node:
                continue
            if color == White:
                #这里也很好改成前序/中序遍历
                stk.append((White, node.right))
                stk.append((Grey, node))
                stk.append((White, node.left))
            else:
                res.append(node.val)
        return res

二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

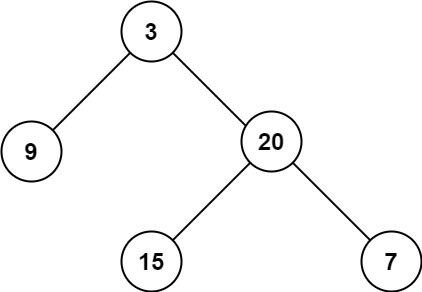
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 [0, 104] 区间内
• -100 <= Node.val <= 100

方法一：深度优先搜索（dfs）

bfs的核心思想是递归实现

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

方法二：广度优先搜索（bfs）

bfs的核心思想是用队列queue实现

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        queue = [root]
        res = 0
        while queue:
            tmp = []
            #每次把一层的节点都放入tmp
            for node in queue:
                if node.left:
                    tmp.append(node.left)
                if node.right:
                    tmp.append(node.right)
            queue = tmp
            res += 1
        return res

翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

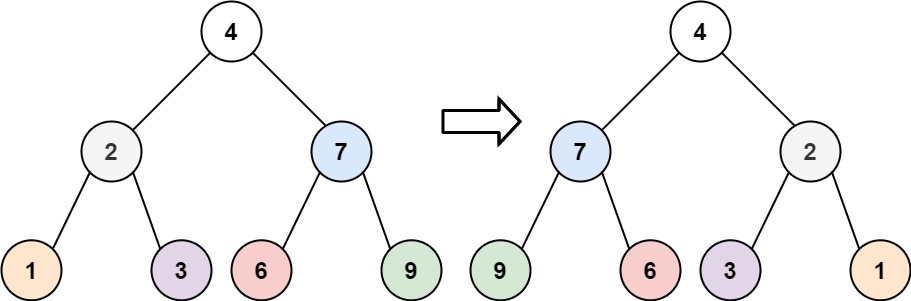
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

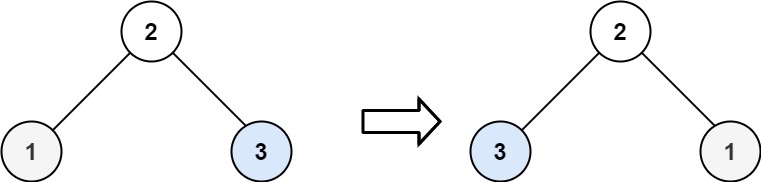
输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

方法一：dfs

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root:
            return

        #先把左右两棵子树交换
        root.left, root.right = root.right, root.left
        #再递归去处理左子树后面的节点以及右子树后面的节点
        self.invertTree(root.left)
        self.invertTree(root.right)
        return root

方法二：bfs

class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root:
            return
        queue = [root]
        while queue:
            tmp = queue.pop(0)
            tmp.left, tmp.right = tmp.right, tmp.left
            if tmp.left:
                queue.append(tmp.left)
            if tmp.right:
                queue.append(tmp.right)
        return root

对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

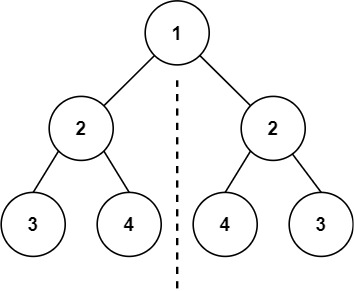
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

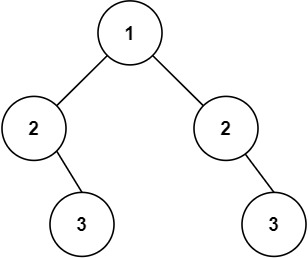
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

方法一：dfs

二叉树对称，就是左右两边相等，所以要递归处理左右两棵子树。

将根节点左子树记为left，根节点右子树记为right。比较left和right的值是否相等，不相等直接返回，相等的话再比较left的的左子节点和right的右子节点，left的右子节点和right的左子节点。

规律：左子树的左子节点=右子树的右子节点

           左子树的右子节点=右子树的左子节点

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        #定义递归函数
        def dfs(left, right):
            #递归终止条件：
            #1.左右两个节点同时为空，true
            if not left and not right:
                return True
            #2.左右两个节点中一个为空，false
            #注意：1和2顺序不能换
            if not left or not right:
                return False
            #3.左右两个节点的值不相等
            if left.val != right.val:
                return False
            #继续递归处理：左左==右右？ 左右==右左？
            return dfs(left.left, right.right) and dfs(left.right, right.left)

        #调用递归函数
        return dfs(root.left, root.right)

方法二：bfs

和递归思想相差不大。

首先从队列中拿出两个节点(left 和 right)比较，相等的话将 left 的 left 节点和 right 的 right 节点放入队列，将 left 的 right 节点和 right 的 left 节点放入队列
 

class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        #节点数目的取值范围[1, 1000]，所以先判断一下是不是只有一个节点
        if not root.left and not root.right:
            return True
        queue = [root.left, root.right]
        while queue:
            #把队列中前两个节点取出来
            left = queue.pop(0)
            right = queue.pop(0)
            #和dfs一样的判断过程
            if not left and not right:
                continue #这里不返回true，因为可能刚比较完左左和右右，还没有比较左右和右左
            if not left or not right:
                return False
            if left.val != right.val:
                return False
            #下面之所以这样放是因为每次比较的时候都是取queue的前两个节点来比较
            #再把 左左 右右 放进队列
            queue.append(left.left)
            queue.append(right.right)
            #把 左右 右左 放进队列 
            queue.append(left.right)
            queue.append(right.left)
        return True

因为本题给的节点数目的范围是[1，1000]，所以代码里我没有判断root是否为空的情况

二叉树的直径

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

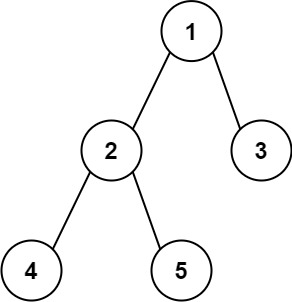
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 104] 内
• -100 <= Node.val <= 100

dfs

直径等于该路径上节点的个数减一。

而一个节点的深度等于从该节点到其叶子节点的所有节点的个数。

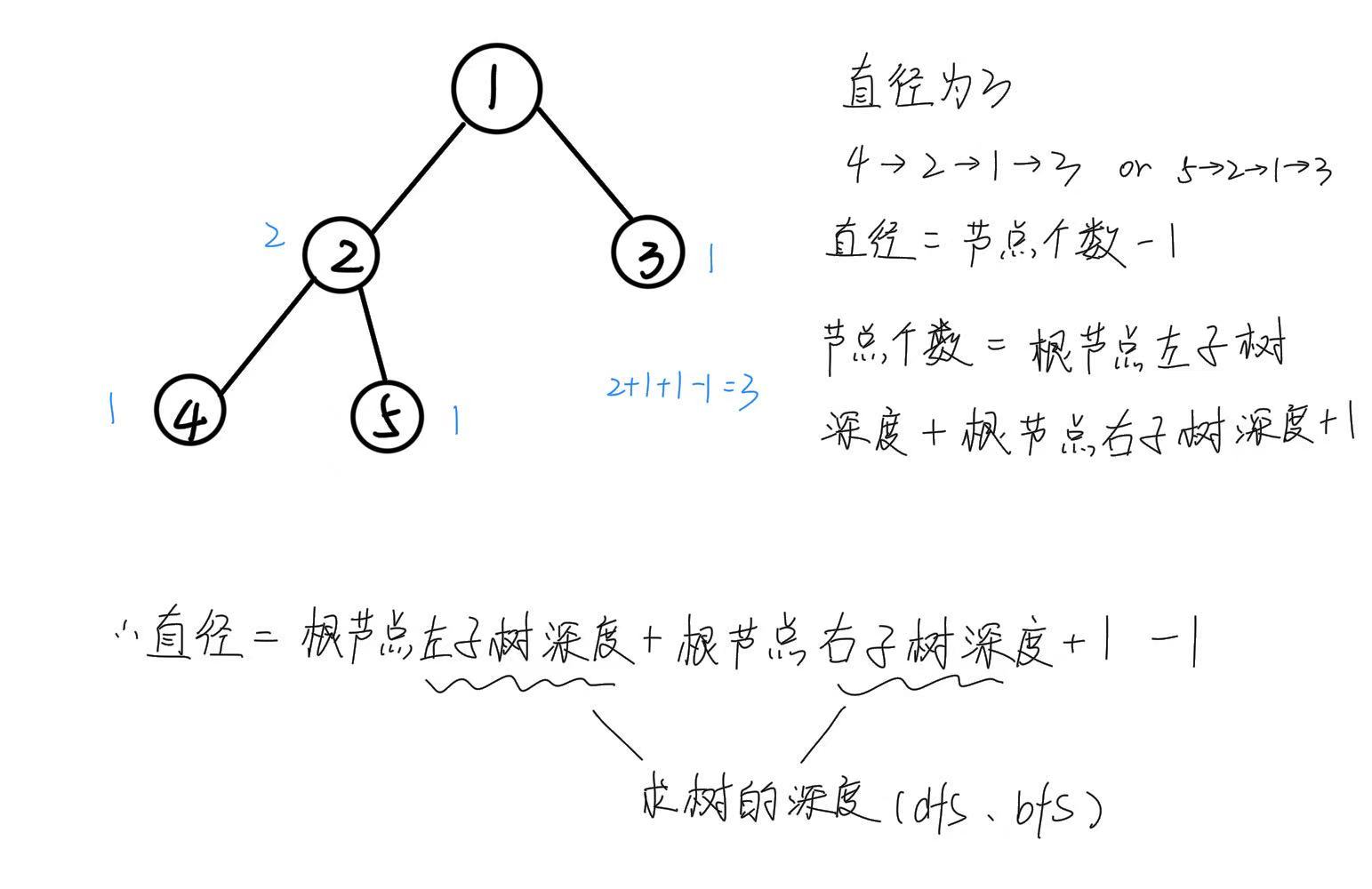
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        #ans为路径上节点的数量。根据节点的范围，最少有一个节点
        self.ans = 1
        #dfs求深度以及更新ans
        def dfs(root):
            if not root:
                return 0
            l = dfs(root.left)
            r = dfs(root.right)
            self.ans = max(self.ans, l + r + 1) #更新最大节点数量
            return max(l, r) + 1 #求节点深度
        dfs(root)
        return self.ans - 1

bfs比较麻烦，先不想了

二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

bfs

本题比较简单，直接用bfs

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        res, q = [], deque()
        q.append(root)
        while q:
            tmp = []
            for _ in range(len(q)):
                node = q.popleft()
                tmp.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            res.append(tmp)
        return res

将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

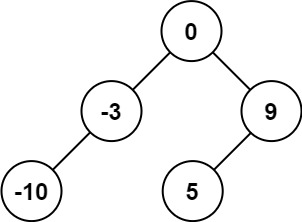
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

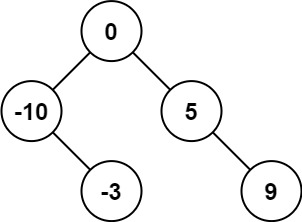
示例 2：

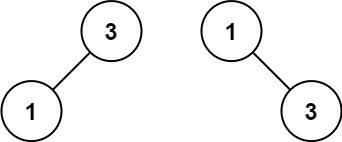
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

基本概念

二叉搜索树（BST）

二叉搜索树（BST，Binary Search Tree）的本质是带有序规则的二叉树，即左小右大的二叉树。其所有节点都满足：

        1.左子树中所有节点的值＜当前节点的值

        2.右子树中所有节点的值＞当前节点的值

平衡二叉搜索树（Self-Balanced BST）

平衡二叉搜索树首先是一棵二叉搜索树，在此基础上增加了平衡条件：

        树上所有节点的 |左子树高度-右子树高度| ≤ 1

  例子：AVL树，红黑树，B树

中序遍历+递归

题目分析：二叉搜索树的中序遍历就是升序序列，所以题目给的数组可以看成是二叉搜索树的中序遍历。

但是给定二叉搜索树的中序遍历不能确定唯一的一棵二叉搜索树，因为任意一个数字都可以作为BST的根节点

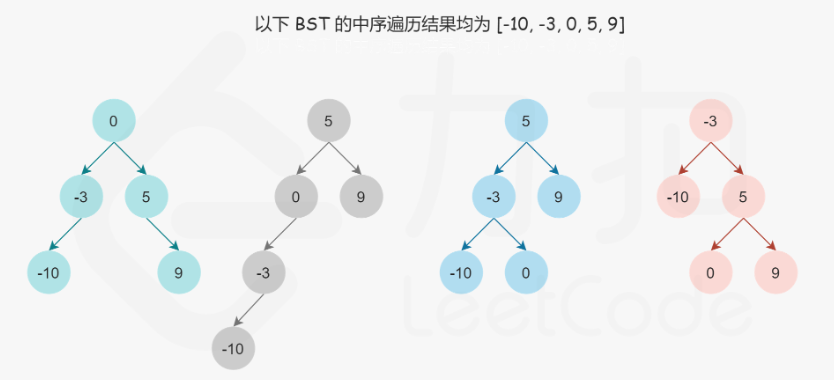
但是即使增加了高度限制，使其成为平衡二叉搜索树，结果也不是唯一的。

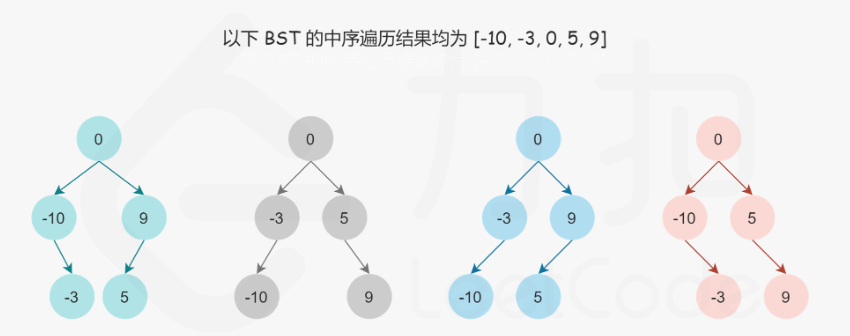
为实现平衡二叉搜索树，直观的看就是每次选择数组的中间数字作为根节点，数组长度是奇数，中间数字是唯一的，数组长度是偶数，中间位置做遍的数字或中间位置右边的数字作为根节点都行。

确定好根节点后，左子树和右子树的处理过程一样，所以递归处理。

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:

        if not nums:
            return None

        mid = len(nums)//2
        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[0: mid])
        root.right = self.sortedArrayToBST(nums[mid + 1: ])

        return root

验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 严格小于 当前节点的数。
• 节点的右子树只包含 严格大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

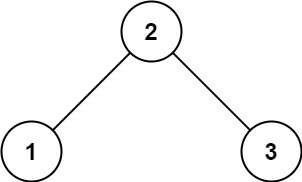
输入：root = [2,1,3]
输出：true

示例 2：

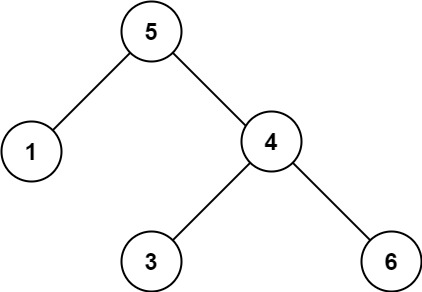
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

方法一：直接DFS递归判断

之前我的一个错误思路是没有用 [lower，upper] 去维护一个上界下界，每次递归都是只和当前root的值去比较，这就导致只检查了左右孩子而没有考虑左右子树

学到了python定义无穷的方式： 正无穷 float('inf')    负无穷 float('-inf')

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        #错误想法
        # def dfs(root):
        #     if not root:
        #         return
        #     if root.left.val > root.val:
        #         return False
        #     if root.right.val < root.val:
        #         return False
        #     self.isValidBST(root.left)
        #     self.isValidBST(root.right)

        def dfs(root, lower = float('-inf'), upper = float('inf')):
            if not root:
                return True
            if root.val >= upper or root.val <= lower:
                return False
            if not dfs(root.left, lower, root.val):
                return False
            if not dfs(root.right, root.val, upper):
                return False
            return True
        return dfs(root)

方法二：DFS中序遍历，序列是否升序判断

二叉搜索树的中序遍历是一个升序的序列，所以可以中序遍历此二叉树，比较当前节点的值与前一个遍历到的节点的值的大小。

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        #记录前一个节点
        self.prv = None
        #dfs中序遍历
        def inorder(root):
            if not root:
                return True
            #递归左子树
            if not inorder(root.left):
                return False
            #比较当前节点的值和上一个节点的值
            if self.prv and root.val <= self.prv.val:
                return False
            self.prv = root #更新prv
            #递归右子树
            if not inorder(root.right):
                return False
            return True
        
        return inorder(root)

二叉搜索树中第K小的元素

中序遍历

很容易想到的思路：因为BST的中序遍历序列是升序的

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        def inorder(root, res):
            if not root:
                return
            inorder(root.left, res)
            res.append(root.val)
            inorder(root.right, res)
        
        res = []
        inorder(root, res)
        return res[k - 1]

大神优化后的，不需要全部遍历

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        def dfs(root):
            if not root:
                return
            dfs(root.left)
            if self.k == 0:
                return
            self.k -= 1
            if self.k == 0:
                self.res = root.val
            dfs(root.right)
        self.k = k
        dfs(root)
        return self.res

二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

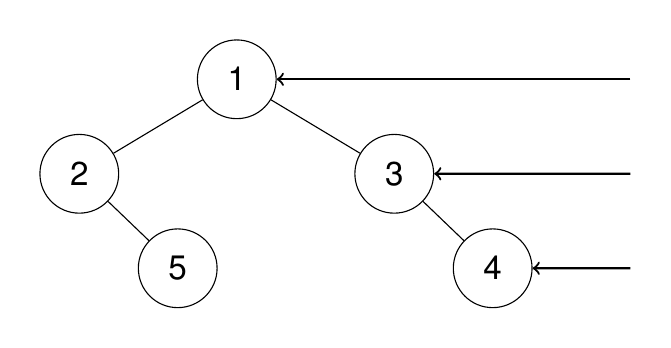
示例 2：

输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

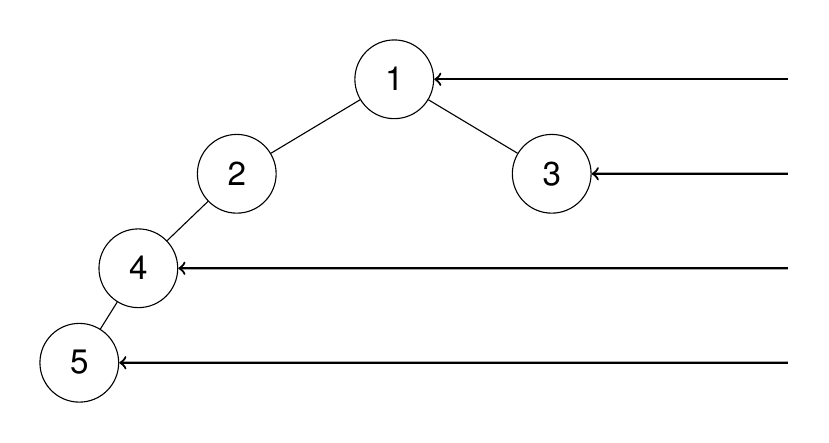
示例 3：

输入：root = [1,null,3]

输出：[1,3]

示例 4：

输入：root = []

输出：[]

提示:

• 二叉树的节点个数的范围是 [0,100]
• -100 <= Node.val <= 100 

bfs

层序遍历的方法很好想到，每到新的一层，从右到左遍历元素，最先遍历到的元素就是最右边的节点，则加答案里

class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        ans = []
        q = deque([root])
        while q:
            ans.append(q[0].val)
            n = len(q)
            for _ in range(n):
                node = q.popleft()
                if node.right:
                    q.append(node.right)
                if node.left:
                    q.append(node.left)
        return ans

dfs

思路一样，每次都是先访问柚子树

class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        self.ans = []

        def dfs(root, depth):
            if not root:
                return
            if depth == len(self.ans):
                self.ans.append(root.val)
            dfs(root.right, depth + 1)
            dfs(root.left, depth + 1)

        dfs(root, 0)
        return self.ans

二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

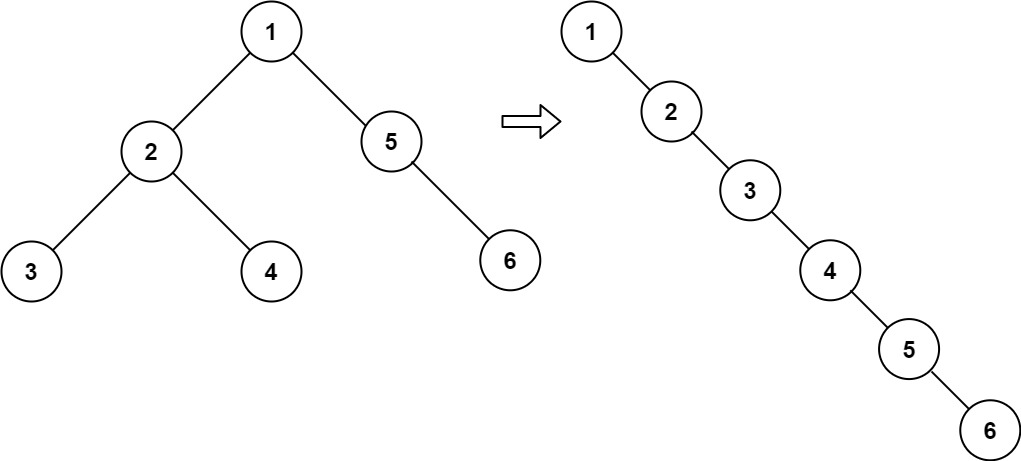
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

先序遍历和链表展开分着进行

空间复杂度O(n)

class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        preorder = []

        def dfs(root):
            if not root:
                return
            preorder.append(root)
            dfs(root.left)
            dfs(root.right)

        dfs(root)
        n = len(preorder)

        for i in range(1, n):
            cur = preorder[i]
            prev = preorder[i - 1]
            prev.left = None
            prev.right = cur

寻找前驱节点

空间复杂度O(1)

从根节点开始，如果根节点存在左子树，那就找左子树最下面的最右边的节点，然后把根节点的右子作为此节点的右子树，之后把根节点的右子树更新为左子树，左子树更新为。后边继续往下遍历，更新节点。

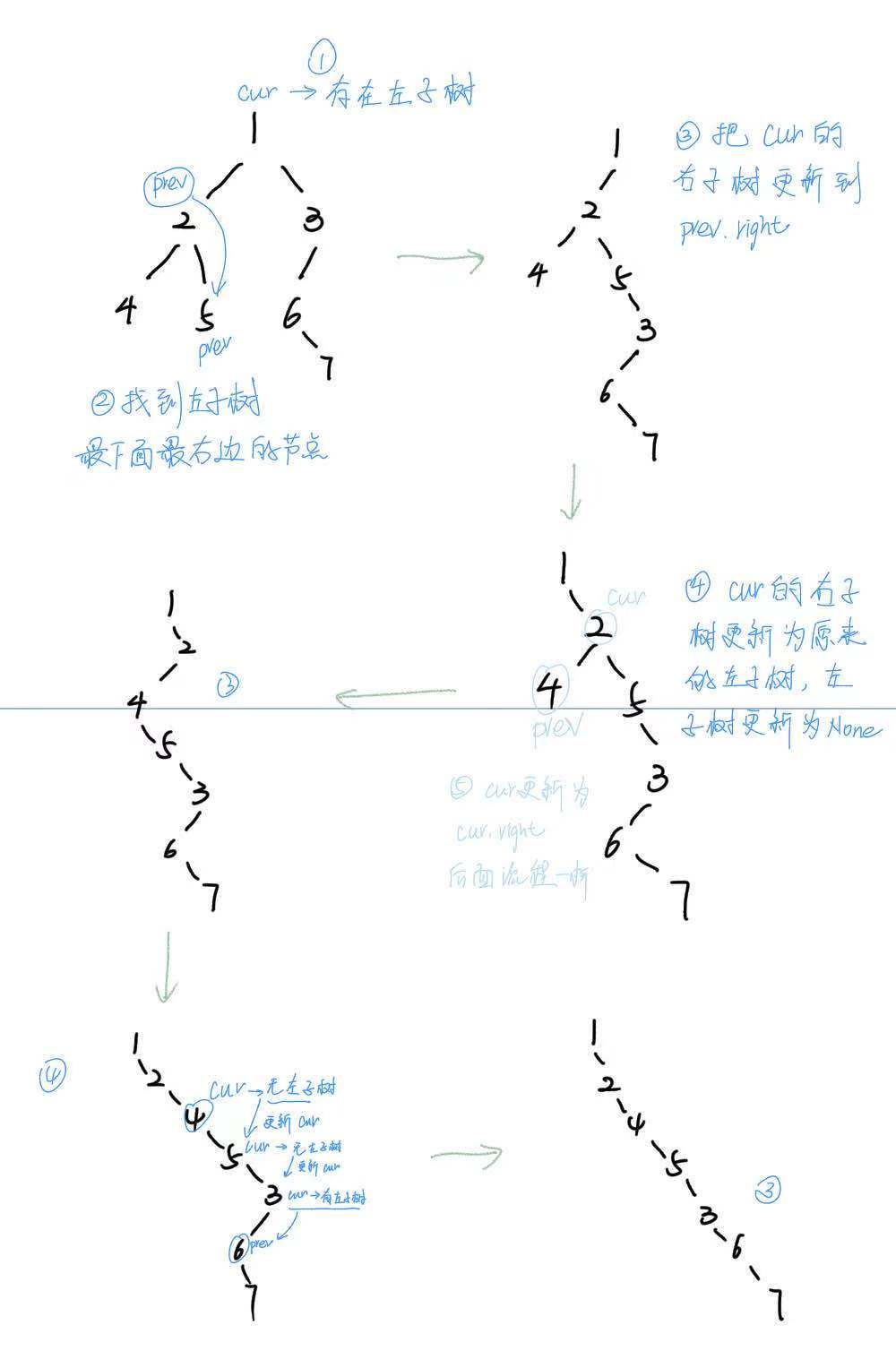
class Solution:
    def flatten(self, root: Optional[TreeNode]) -> None:
        """
        Do not return anything, modify root in-place instead.
        """
        cur = root
        while cur:
            if cur.left:
                prev = cur.left
                while prev.right:
                    prev = prev.right
                prev.right = cur.right
                cur.right = cur.left
                cur.left = None
            cur = cur.right

从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

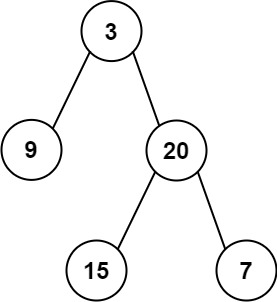
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均 无重复 元素
• inorder 均出现在 preorder
• preorder 保证 为二叉树的前序遍历序列
• inorder 保证 为二叉树的中序遍历序列

递归

前序遍历：【根】【左子树】【右子树】

中序遍历：【左子树】【根】【右子树】

前序遍历的第一个元素就是根节点，则根据根节点的值在中序遍历序列中定位根节点的位置，该位置左边的数字都属于左子树，右边的数字都属于右子树，又因为前序和中序中左子树节点数量、右子树节点数量都是相等的，所以也可以确定前序遍历哪些数字属于左子树，哪些属于右子树。

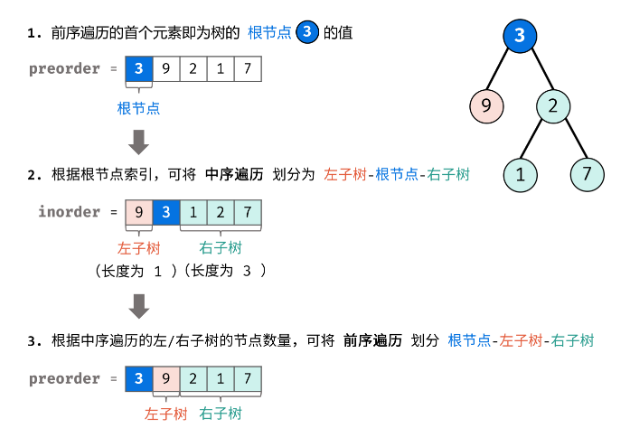
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        #这个是非常直接的思路
        if not preorder:
            return None
        root = TreeNode(preorder[0])
        mid = inorder.index(preorder[0])
        root.left = self.buildTree(preorder[1: mid + 1], inorder[0:mid])
        root.right = self.buildTree(preorder[mid+1:], inorder[mid+1:])
        return root

递归优化版

利用哈希表存储中序遍历中每个值的索引，不用每次递归的时候再次用inorder.index了

root是当前子树根节点在前序遍历中的索引，left是当前子树在中序遍历中的左边界，right是当前子树在中序遍历中的右边界。

递归的时候：当前子树的左子树的根节点在前序遍历中的索引是root+1，右子树根节点在前序遍历中的索引=根节点位置+左子树长度+1 = root + i - left + 1。

当前子树根节点在中序遍历中的索引为i，则左子树节点索引为[left, i - 1]，右子树节点索引为[i + 1, right]，所以左子树长度为 i - 1 - left + 1 = i - left。

递归停止条件是left > right

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        #哈希表存储中序遍历中每个值的索引
        dic = {}
        n = len(inorder)
        for i in range(n):
            dic[inorder[i]] = i

        def helper(root, left, right):
            #递归终止条件
            if left > right:
                return
            node = TreeNode(preorder[root])
            i = dic[preorder[root]]
            #递归处理左右子树
            node.left = helper(root + 1, left, i - 1)
            node.right = helper(root + i - left + 1, i + 1, right)
            return node
        
        #初始，根节点在前序中的索引是0（第一个元素）
        #中序遍历中左边界0，右边界len - 1
        return helper(0, 0, n - 1)

路径总和III

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

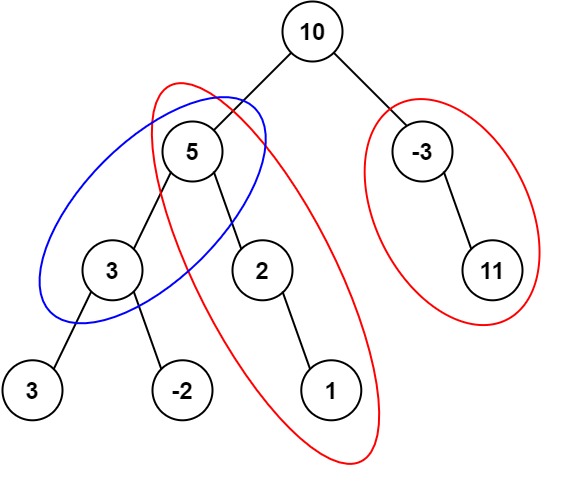
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

• 二叉树的节点个数的范围是 [0,1000]
• -109 <= Node.val <= 109 
• -1000 <= targetSum <= 1000 

前缀和+哈希表+dfs回溯

目标和为targetSum，当前节点为cur，其前缀和为S。

如果存在某个祖先节点的前缀和为S - targetSum，则说明从该祖先节点的下一个节点到当前节点的路径和为targetSum（因为 S - (S - targetSum) = targetSum）

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        #哈希表存储前缀和的值及其出现的次数
        prefix = defaultdict(int)
        prefix[0] = 1 #初始化，前缀和为0的情况出现1次

        def dfs(node, sum):
            if not node:
                return 0
            res = 0
            sum += node.val #更新前缀和
            res += prefix[sum - targetSum]
            prefix[sum] += 1
            res += dfs(node.left, sum)
            res += dfs(node.right, sum)
            prefix[sum] -= 1 #回溯
            return res

        return dfs(root, 0) 

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

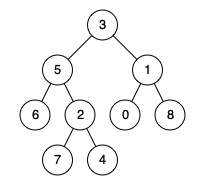
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点5和节点1的最近公共祖先是节点3 。

示例 2：

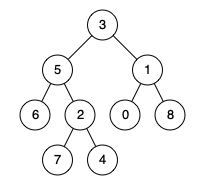
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点5和节点4的最近公共祖先是节点5。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

dfs递归+回溯

递归遍历二叉树，通过「自底向上」（保证深度最深）的判断逻辑，确定 p 和 q 的公共祖先。核心逻辑是：

• 若当前节点的左子树包含 p 或 q，且右子树也包含 p 或 q，则当前节点就是 LCA；
• 若只有左子树包含 p 或 q，则左子树的结果就是 LCA；
• 若只有右子树包含 p 或 q，则右子树的结果就是 LCA；

递归终止条件

if root == q or root == p or root == None:
    return root

• 如果当前节点root是 p、是 q，或者是None（空节点），直接返回root。
• 作用：
  • 若root是 p 或 q：说明在当前路径上找到了目标节点，返回它（供上层判断）；
  • 若root是None：说明当前路径上没有 p 或 q，返回空（表示未找到）。

递归遍历左右子树

left = self.lowestCommonAncestor(root.left, p, q)  # 左子树中寻找p/q的结果
right = self.lowestCommonAncestor(root.right, p, q)  # 右子树中寻找p/q的结果

• 递归处理当前节点的左子树和右子树，分别得到左子树中是否包含 p/q 的结果（left），以及右子树中是否包含 p/q 的结果（right）。
• 注意：left和right的返回值可能是None（子树中无 p/q），也可能是 p、q，或它们的公共祖先。

判断当前节点是否为LCA

if left and right:
    return root  # 左、右子树各包含一个目标节点 → 当前节点是LCA
if left == None and right:
    return right  # 只有右子树有目标节点 → 右子树的结果是LCA
elif left and right == None:
    return left  # 只有左子树有目标节点 → 左子树的结果是LCA
else:
    return None  # 左右子树都没有目标节点 → 返回空

1. left和right都不为空：说明 p 和 q 分别在当前节点的左子树和右子树中（左子树找到一个，右子树找到另一个），因此当前节点root就是它们的最近公共祖先。
2. left为空，right不为空：说明 p 和 q 都在右子树中（右子树的结果已经是它们的公共祖先），因此返回right。
3. left不为空，right为空：类似情况 2，p 和 q 都在左子树中，返回left。
4. left和right都为空：说明当前子树中既没有 p 也没有 q，返回空。

完整代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if root == p or root == q or root == None:
            return root
        left = self.lowestCommonAncestor(root.left, p ,q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        if not left and right:
            return right
        if left and not right:
            return left
        if not left and not right:
            return None

二叉树中的最大路径和

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

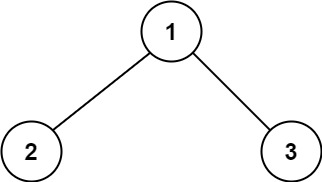
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

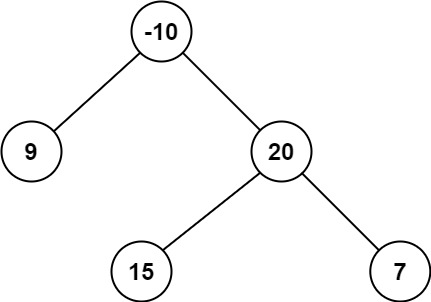
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

dfs递归+回溯

maxsum是最大路径和，dfs函数中的返回值是以当前子树的root为开始节点的最长的路径和（智能是该root的节点的值+max（左子树的值，右子树的值））

当节点的值是负数的时候，当成0处理，因为不会把该节点加进总路径

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.maxsum = root.val
        def dfs(root):
            if not root:
                return 0
            left = dfs(root.left)
            right = dfs(root.right)
            left = max(left, 0)
            right = max(right, 0)
            self.maxsum = max(self.maxsum, left + right + root.val)
            return max(left, right) + root.val
        dfs(root)
        return self.maxsum