机器学习——支持向量机

一.支持向量机

支持向量机介绍

支持向量机（Support Vector Machine，SVM）是一种强大的监督式学习算法，常用于分类和回归分析。它在许多机器学习任务中都表现出色，尤其在具有复杂边界和高维特征空间的数据集上效果显著。经常用在二分类等问题当中。SVM 还可以用于回归分析，即支持向量回归（Support Vector Regression，SVR）。与分类不同，SVR 试图找到一个超平面，使得样本点与该超平面的距离尽可能小，同时还要保持尽可能多的样本点在超平面的间隔之内。

工作原理

SVM 的核心思想是在特征空间中找到一个超平面，能够将不同类别的样本点正确地分开。在二维空间中，这个超平面就是一条直线；在更高维空间中，它可以是一个平面、超平面或者更高维的结构。SVM 最大化了样本到超平面的间隔，使得分类的鲁棒性和泛化能力更强。

支持向量机通俗理解

其实支持向量机可以这样理解：

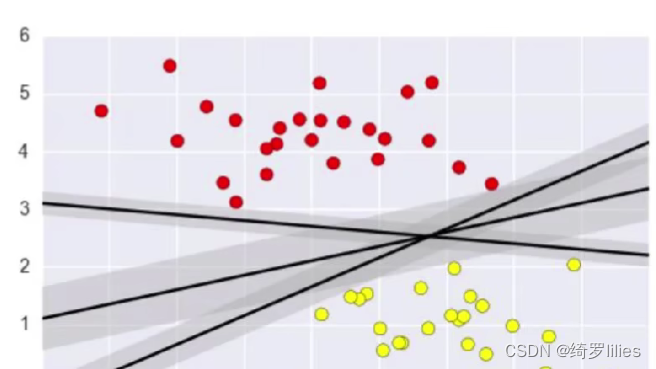
如图所示的三条黑线，均可以对样本进行分类达到效果，但是军=都不是最佳的方案。我们可以这样理解支持向量机，就是把图中的要分类之间的点看成地雷，要让一排排的军队安全的通过这里，是不是要找到一条最优化的路线，使得军队距离最近距离的地雷是最远的，这个过程就是支持向量机的理解。

支持向量机优缺点

支持向量机是一种用于分类和回归分析的监督式学习模型，其优点和缺点如下：

优点：
（1）在高维空间中具有较好的泛化能力，可以处理高维数据；
（2）可以处理非线性数据，借助核函数可以将数据映射到更高维的空间进行分类；
（3）在数据较少的情况下表现较好，因为SVM利用支持向量进行决策，不需要依赖整个数据集；
（4）对异常值的鲁棒性较强，并且在较噪声的情况下表现较好。

缺点：
（1）对超大规模数据集的训练不太友好，由于其时间复杂度为O(n^3)，一旦数据集规模变大，训练时间可能会非常长；
（2）对缺失数据敏感，需要对数据进行预处理以处理缺失值；
（3）对于多类分类问题需要进行多次二进制分类，比较麻烦；
（4）对参数的选择和核函数的选择比较敏感，需要通过交叉验证等方法进行调参。

二.支持向量机相关概念

支持向量

支持向量指的是在支持向量机分类中，那些离超平面最近的样本点。它们是对构建超平面有重要影响的样本点，因为它们决定了超平面的位置和方向。更具体地说，支持向量是在最大化间隔的过程中起作用的，它们是距离超平面最近的点，这些点的法向量与超平面的切线相平行。支持向量机的训练过程就是找到这些支持向量，并根据它们来确定最佳的超平面，使得间隔最大化。在分类任务中，支持向量机的决策边界是由这些支持向量所确定的。持向量在支持向量机算法中发挥了关键作用，它们是决定分类边界的重要因素。通过选择合适的支持向量，支持向量机能够构建出一个有效的分类器，并且对于新的未见过的数据也能有很好的泛化能力

如图中所示的圈起来的X和圈起来的—就是支持向量。

距离

在支持向量机（SVM）中，距离是一个重要的概念，它指的是样本点到超平面的距离。在SVM中，距离的计算有多种不同的方式，具体取决于所使用的核函数和超平面的定义。

在线性SVM中，超平面可以用一个线性方程表示： w T x − b = 0 \mathbf{w}^T\mathbf{x} - b = 0