代码随想录Day4 | 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、面试题 02.07. 链表相交、142.环形链表II

最新推荐文章于 2025-12-26 21:53:33 发布

原创最新推荐文章于 2025-12-26 21:53:33 发布 · 1k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

24. 两两交换链表中的节点

这道题目要采用虚拟头结点的操作，以便统一交换规则。每次都要找到要交换的两个结点的前一个结点，这样才更好操作。如果不用虚拟头结点，对待头结点还要单独处理。

交换相邻元素的三个步骤：

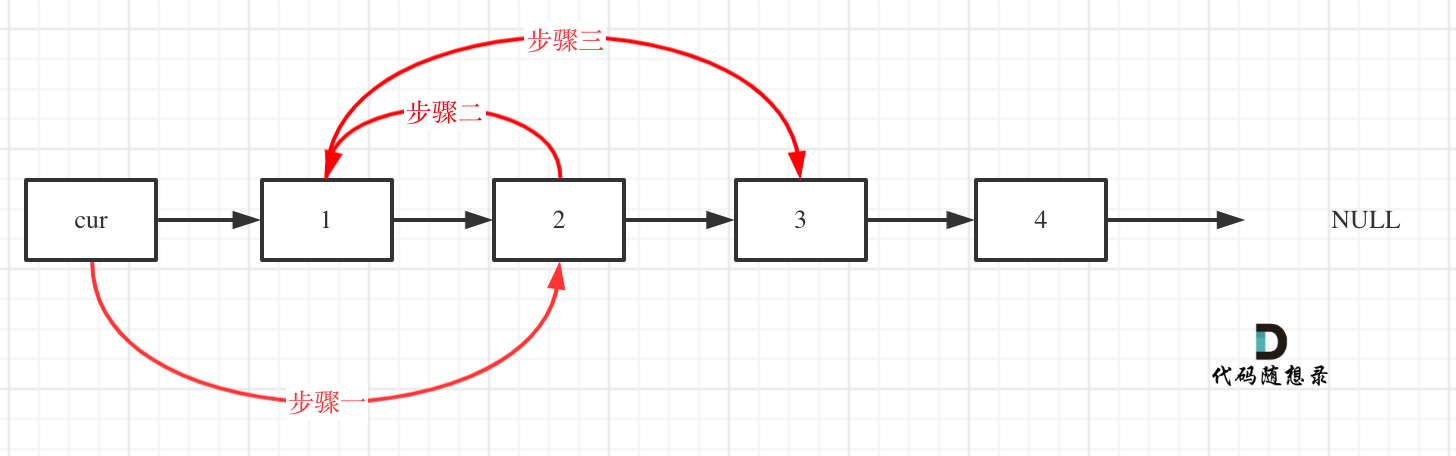
24.两两交换链表中的节点1

注意：要记录两个临时结点（以图中为例，要记录1和3两个结点），因为在执行完步骤1后，cur指向2结点，1结点无法访问到；执行完步骤二后，2结点指向1结点，3结点无法访问到。

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyhead=new ListNode(0);
        dummyhead->next=head;
        ListNode* cur=dummyhead;
        while(cur->next!=NULL&&cur->next->next!=NULL)
        {
           ListNode* tmp=cur->next;
           ListNode* tmp1=cur->next->next->next;
           cur->next=cur->next->next;
           cur->next->next=tmp;
           tmp->next=tmp1;
           cur=cur->next->next;
        }
        head=dummyhead->next;
        delete dummyhead;
        return head;
    }
};

19.删除链表的倒数第N个节点

算法思路： 要找到被删除结点的前一个位置才能进行删除操作，定义快慢指针，都指向虚拟头结点。先让快指针走(n+1)步，然后让快慢指针同时移动，当快指针指向NULL的时候，慢指针指向的就是要删除结点的前一个位置。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummyhead=new ListNode(0);
        dummyhead->next=head;
        ListNode* fast=dummyhead;
        ListNode* slow=dummyhead;
        n++;
        while(n--&&fast!=NULL)
        {
            fast=fast->next;
        }
        while(fast!=NULL)
        {
            fast=fast->next;
            slow=slow->next;
        }
        ListNode* tmp=slow->next;
        slow->next=slow->next->next;
        delete tmp;
        head=dummyhead->next;
        delete dummyhead;
        return head;
    }
};

面试题 02.07. 链表相交

相交：是指同一个结点，即同一个地址存储的同一个结点，并不是指结点的数值相等。所以在比较是否是统一结点时应该比较的是两个链表指针指向的地址，而不是数值。

算法思路： 两个链表的长度不一定相等，但相交部分一定是后部分，即如果从某个结点开始相交，则后面的部分一定都相交。因此要先求出两个链表长度的差值，让较长的那个链表后移这个差值，令两个链表的尾部对齐。此时我们就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。

也就是说，如果两个链表的当前结点，后面的节点数量都不一样，那当前结点一定不是交点。

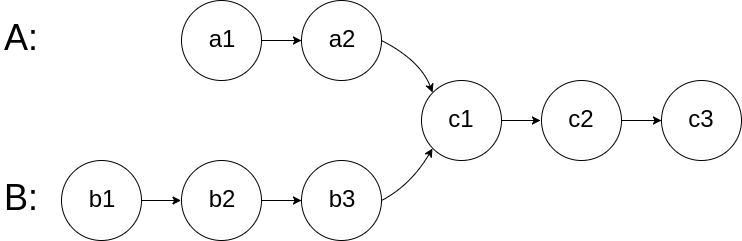
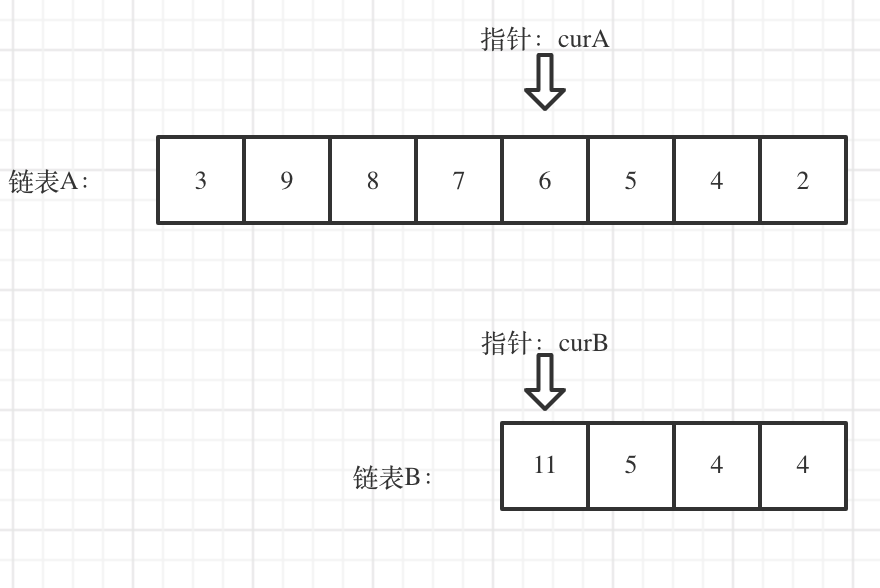
面试题02.07.链表相交_2

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* curA=headA;
        ListNode* curB=headB;
        int lenA=0,lenB=0;
        while(curA!=NULL)
        {
            lenA++;
            curA=curA->next;
        }
        while(curB!=NULL)
        {
            lenB++;
            curB=curB->next;
        }
        curA = headA;
        curB = headB;
        if(lenB>lenA)
        {
            swap(lenA,lenB);
            swap(curA,curB);
        }
        int gap=lenA-lenB;
        while(gap--)
        {
            curA=curA->next;
        }
        while(curA!=NULL)
        {
            if(curA==curB)
            {
                return curA;
            }
            curA=curA->next;
            curB=curB->next;
        }
        return NULL;
    }
};

142.环形链表II

如何判断是否有环？

用快慢指针，快指针每次移动两个结点，慢指针每次移动一个结点，如果快慢指针相遇，则证明有环。（如果没有环，快指针始终比慢指针快，不可能相遇）且快慢指针一定会在环里相遇。

为什么快慢指针一定会相遇？

fast会先进入环，slow会后进入环。两者都进入环后，相当于fast每次向slow移动一个结点，fast在追赶slow的过程。因此一定是会相遇的，因为是一个结点一个结点地去靠近的。

如何找到环的入口？

假设从头结点到环形入口节点的节点数为x。环形入口节点到 fast指针与slow指针相遇节点节点数为y。从相遇节点再到环形入口节点节点数为 z。如图所示：

那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针，（y+z）为一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点，所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个（x+y）: x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示头结点到环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n(y+z)中提出一个（y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

这就意味着，从头结点出发一个指针，从相遇节点也出发一个指针，这两个指针每次只走一个节点，那么当这两个指针相遇的时候就是环形入口的节点。

为什么慢指针一定是在第一圈被追上了？

因为快指针的速度是慢指针速度的2倍，假设慢指针在第一圈的时候没被追上，则慢指针走到第一圈终点时，快指针已经走了两圈，所以一定可以追上。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast=head;
        ListNode* slow=head;
        while(fast!=NULL&&fast->next!=NULL)
        {
            fast=fast->next->next;
            slow=slow->next;
            if(fast==slow)
            {
                ListNode* index1=fast;
                ListNode* index2=head;
                while(index1!=index2)
                {
                    index1=index1->next;
                    index2=index2->next;
                }
                return index1;
            }
        }
        return NULL;
    }
};