深度学习入门——神经网络

神经网络思想

        神经网络是人工神经网络(Artificial Neural Network,ANN)的简称,是深度学习算法的核心，神经网络受到人脑的启发，可模仿生物神经元相互传递信号的方式。

        高中生物中，我们学到的神经元之间的信息传递，神经元接受信号，把传入的信息传递给中心部分，这些信息中有兴奋性的和抑制性的，然后细胞体对传入的信息进行汇总，当信号之和到达某一阈值时，细胞体就会做出相应的反应，向与轴突连接的其他神经元传递信号。至此，一次神经元之间的信息传递就完成了。

                

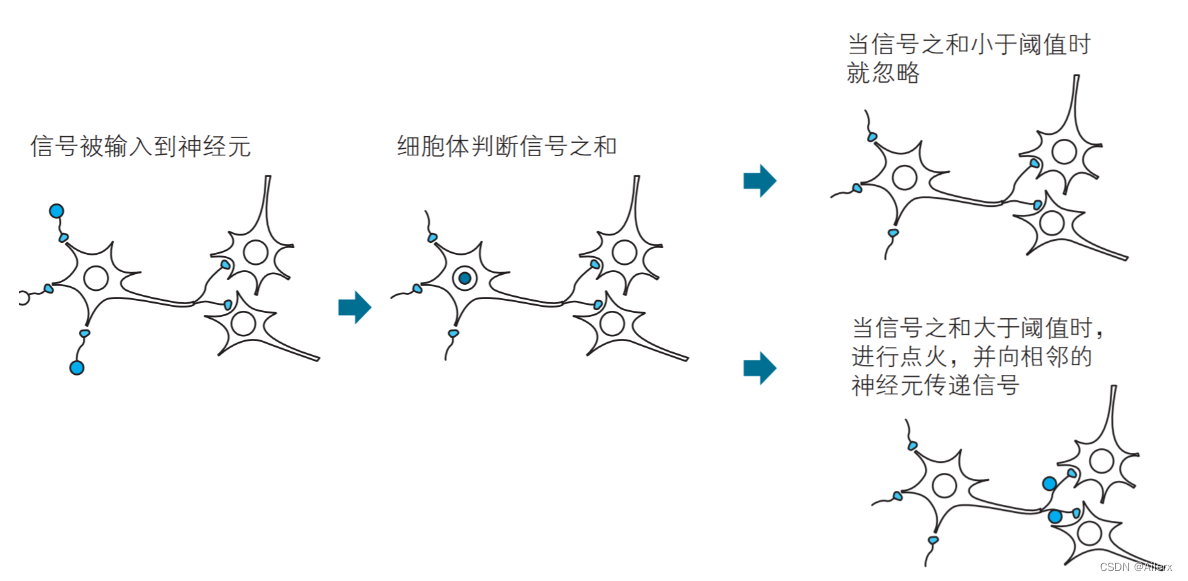
                                                                                  图一

        神经网络的基本思想是：

               

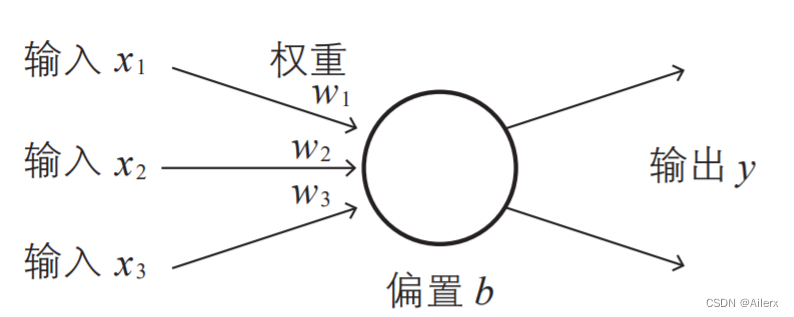
                                        图二

接收一组输入数据，在经过一系列操作后(包括，对输入值进行加权重和偏置以及激活函数处理等操作后)得到我们的输出值，如果输出值达到我们的某一特定预期，就有信息输出，否则无信息输出。

单层神经网络

                        

                                                                                图三

        输出 = 激活函数（权重的加权和 + 偏置）——>    y=a(+++b)  

                                         

                                                                图四

首先对这个公式里提到的几个概念进行介绍：

        激活函数（Activation Function）：它是一种数学函数，应用于神经网络中的每个神经元，用于确定神经元的输出。它将神经元的输入总和转换为神经元的输出值，通常通过引入非线性变换来增加神经网络的表达能力。常见的激活函数有，Sigmoid,ReLu,Tanh，等等，后续会单出一篇文章进行详细的介绍。

        权重（weights）：权重决定了每个神经元对输入的重要性，通过不断调整权重，神经网络可以学习到适应任务的特征表示。

        偏置（bias）：偏置是一个常数项，它与神经元的输入加权求和相结合，并通过激活函数进行非线性变换。偏置的作用是为每个神经元引入一个偏移量，使得神经元能够更好地拟合数据和提取特征

具体过程：

1. 初始化权重和偏置：为每个输入特征设置一个对应的权重，并且为输出层设置一个偏置。这些权重和偏置可以随机初始化。
2.  前向传播：将输入数据传递到神经网络中。对于每个输入特征，乘以对应的权重，并将它们求和，然后加上偏置。这个求和的结果将作为输入层神经元的输出。对这个值进行激活函数处理，得到真正的输出值。
3. 计算损失：根据输出层的预测结果和真实标签，计算损失函数。损失函数用于衡量预测值与真实值之间的差异。
4. 反向传播和参数更新：使用反向传播算法来计算权重和偏置的梯度，进而更新它们的数值。通过链式法则，将损失函数的梯度从输出层向后传播到输入层，并根据梯度下降等优化算法，更新权重和偏置，以减小损失函数的值。
5. 重复步骤2至4：重复执行前向传播、计算损失、反向传播和参数更新的步骤，直到达到预定义的停止条件，如达到一定的训练轮数或损失函数收敛。
6. 预测：经过训练后，使用更新后的权重和偏置对新的输入数据进行前向传播，得到预测结果。                

流程图：

                                

                                                       图五

        需要注意的是，单层神经网络只能解决线性可分的问题，即只能学习线性决策边界。对于复杂的非线性问题，单层神经网络无法进行有效建模，需要使用多层神经网络（深度神经网络）来提高表达能力。

        写在最后：
        后续会出个专栏，用于记录自己在机器学习和深度学习学习到的知识，以及问题。内容或许有很多错误，恳求大家指正。

        参考内容：

                图一，图二来源：涌井良幸，涌井贞美《深度学习中的数学》

                图三来源：阿斯顿·张，李沐《动手学深度学习》