数据结构排序算法笔记（4）

基数排序算法

基数排序(radix sort)的思想是多关键字排序，属于分配式排序。它是通过键值的各个位的值，将要排序的元素分配至某些“桶”中，然后依次收集各个桶内数据，通过分配和收集达到排序的目的。

基数排序是1887年赫尔曼·何乐礼发明的。它是这样实现的：将整数按位数切割成不同的数字，然后按每个位数分别比较。

基数排序算法有两种排序方式：

从个位依次开始排序

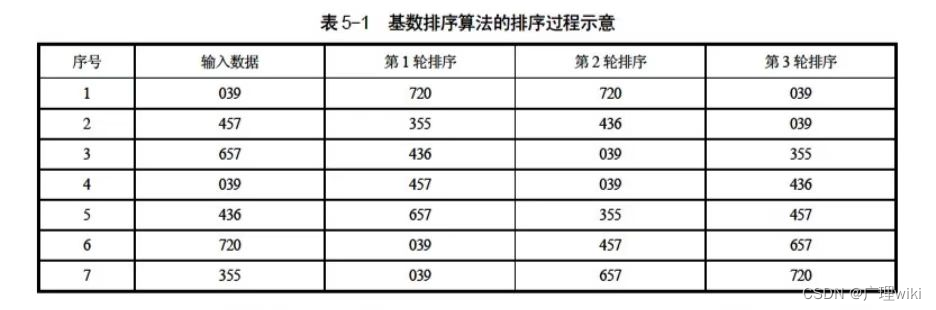
从百位依次开始排序

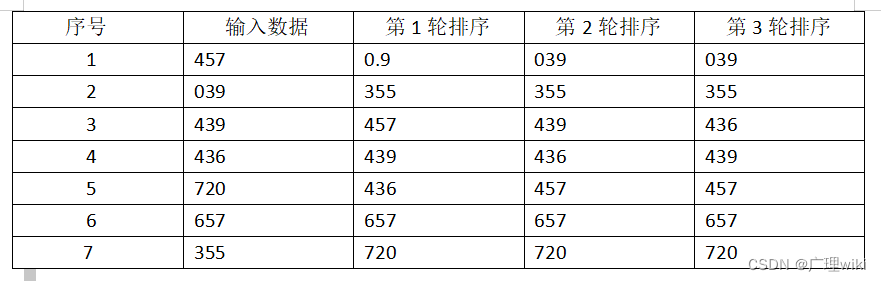
接下来用一个动画来让大家更好地理解吧！

实例演练

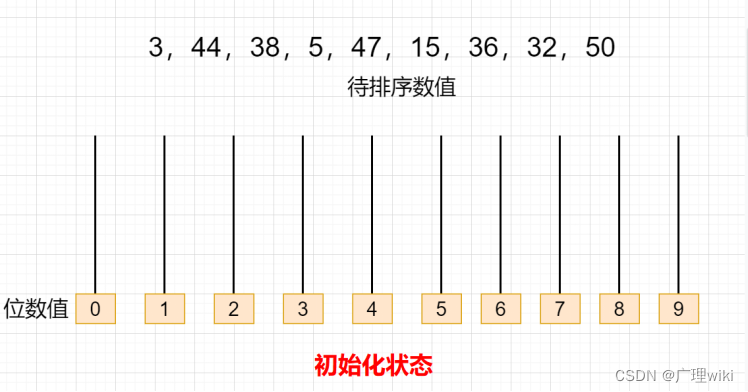
现有如下序列：{3，44，38，5，47，15，36，32，50}，现在要利用基数排序算法对这9个元素进行从小到大的排序，你们认为应该怎么排呢？

1.排序的初始化状态如下图所示：

2. 将这9个元素按个位分配到相应的位置上，如下图所示：

3.将第二步分配好的结果按顺序取出，因为是按个位排序的，所以取出来的元素一定是按个位有序的，如下图所示：

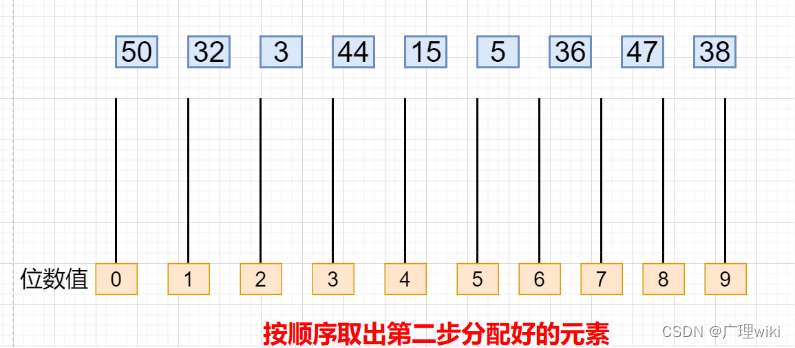
4.将元素按十位放入到相应的位置，上一步的数是按个位有序的，现在按十位放入相应的位置，放入之后，对于每个位置而言，都是大数在上面，小数在下面，如下图所示：

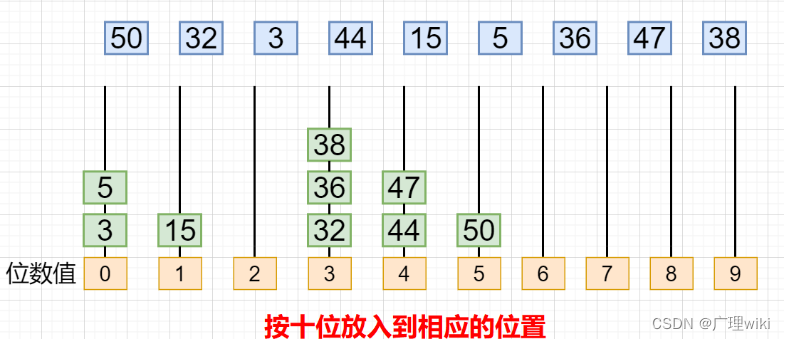
5. 因为是从小到大排序，将元素从左往右，从下到上依次取出，如下图所示：

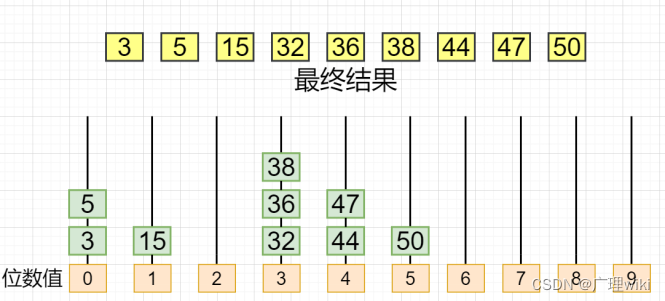
代码实现：

/**
 * @ClassName RadixSortDemo
 * @author: shouanzh
 * @Description 基数排序
 * @date 2022/5/10 20:31
 */
public class RadixSortDemo {
    public static void main(String[] args) {

        int[] array = new int[]{3，44，38，5，47，15，36，32，50};

        radixSort(array);

        System.out.println(Arrays.toString(array)); // [3，5，15，32，36，38，44，47，50]

    }


    /**
     * 基数排序（LSD 从低位开始）
     * @param array 数组
     */
    public static void radixSort(int[] array) {

        // 取得数组中的最大数，并取得位数
        int max = array[0]; // 假设第一个数就是最大的
        for (int item : array) {
            if (item > max) {
                max = item;
            }
        }
        // 最大数是几位数
        int maxLength = (max + "").length();


        // 定义一个二维数组，表示10个桶，每个桶就是一个一维数组，每个桶的长度为array.length
        int[][] buckets = new int[10][array.length];

        // 为了记录每个桶中，实际存放了多少个数据，我们定义一个一维数组来记录各个桶的每次放入的数据个数
        // 比如：bucketElementCounts[0] 记录的就是 buckets[0] 桶存放数据的个数
        int[] bucketElementCounts = new int[10];


        for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
            // 针对每个元素的对应位进行排序处理，第一次是个位，第二次是十位，第三次是百位...
            for (int element : array) {
                // 取出每个元素个位的值
                int digitOfElement = element / n % 10; // 如获取十位数， 978 / 10 = 97 % 10 = 7
                // 放入到对应的桶
                buckets[digitOfElement][bucketElementCounts[digitOfElement]] = element;
                // 桶计数++
                bucketElementCounts[digitOfElement]++;
            }

            // 按照这个桶的顺序(一维数组的下标依次取出数据，放入原来数组)
            int index = 0;
            // 遍历每一个桶，并将桶内数据放入到原数组
            for (int k = 0; k < bucketElementCounts.length; k++) {
                // 如果桶中有数据，才放入到原数组
                if (bucketElementCounts[k] != 0) {
                    // 循环该桶（即第K个一维数组）
                    for (int l = 0; l < bucketElementCounts[k]; l++) {
                        // 取出元素，放入到array
                        array[index] = buckets[k][l];
                        index++;
                    }
                }
                // 处理完毕后，将桶计数bucketElementCounts[k] 清0
                bucketElementCounts[k] = 0;
            }

            System.out.println("第" + (i + 1) + "轮排序：" + Arrays.toString(array));

        }
    }

}

最后我再总结一下排序的稳定性

稳定排序：冒泡排序，插入排序，归并排序，基数排序。

不稳定排序：选择排序，快速排序，希尔排序，堆排序。