《数据结构》二叉树（性质and遍历）

Java冰激凌

已于 2023-01-31 22:47:32 修改

阅读量1.1k

点赞数 21

分类专栏：数据结构 Java 文章标签：数据结构

于 2023-01-30 22:07:48 首次发布

本文链接：https://blog.youkuaiyun.com/m0_69996872/article/details/128808203

版权

Java 同时被 2 个专栏收录

24 篇文章

订阅专栏

数据结构

12 篇文章

订阅专栏

本文深入讲解了二叉树的基本概念，包括满二叉树、完全二叉树的定义及特点，并详细介绍了二叉树的四种遍历方法：先序、中序、后序和层序遍历。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

👑作者主页：Java冰激凌
📖专栏链接：数据结构

目录

编辑

树的定义

概念

树的定义

二叉树的概念

满二叉树

概念

完全二叉树

概念

二叉树的性质

二叉树的遍历

先序遍历

中序遍历

后序遍历

层序遍历

树的定义

概念

树是一种非线性的数据结构

树的定义

子树是不相交的
除了根节点外，每个节点有且仅有一个父节点
一颗N个节点的树有N+1条边

二叉树的概念

二叉树的每个节点要么有0个孩子，要么有1个孩子，要么有2个孩子,也就是说二叉树的节点数量为X （0 <= x <= 2）
一棵树如果是二叉树，那么它的每一颗子树都为二叉树（如果存在不是二叉树的情况则整棵树便不是二叉树）
二叉树的子树有左（left）右（right）之分，次序不能颠倒，因此二叉树是有序树（此处提到的有序不是代表节点中值的大小有序，仅仅是有左右顺序之分）

上述的描述可能还是不够形象的下图为手绘的二叉树图大概参考一下

满二叉树

概念

一个二叉树如果每一层的结点数都达到最大则这个二叉树就是满二叉树也就是说如果一颗二叉树的层数为K 且结点总数是2^K-1 则它就是满二叉树，次数计算结点个数也可以看做应等比数列

光看上述的概念还是比较抽象的我们来简单的上几张图

上图不是一个满二叉树因为没有达到层数节点的最大值

上述图为满二叉树因为每层节点数量都达到了最大值

上述图不是满二叉树还是因为每层节点数量没有达到最大值

总结：其实分辨一棵树是否为满二叉树很简单只要看每层节点都存在即可分辨

完全二叉树

概念

完全二叉树是由满二叉树而引出来的，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。因为完全二叉树是由满二叉树引出来的，所以满二叉树也是完全二叉树的一种

那么什么是完全二叉树的形呢？我们还是以图来认识一下

上图不是一颗完全二叉树因为二叉树的排列是左子树右子树如果有一颗右子树不存在那么后面再没有任何节点（认真悟）

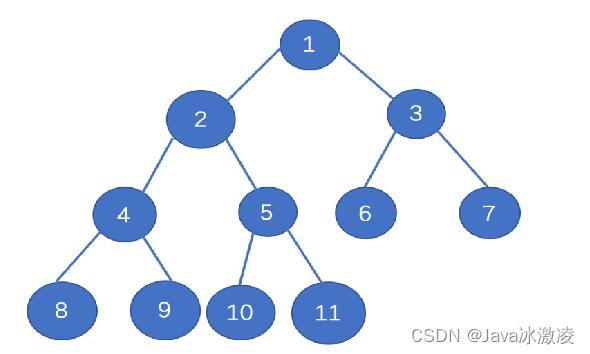
上图是一颗完全二叉树满足完全二叉树的所有性质

上图也是一颗完全二叉树当然也是一颗满二叉树我们在概念中提到的因为完全二叉树是满二叉树引出的所以满二叉树也是属于完全二叉树

二叉树的性质

其中第三条性质是最有趣的我们来分析一下第三条性质

对于任何一颗二叉树来说度为0的节点永远都比度为2的节点多一个

推导公式如下：

假设二叉树有N个节点那么一颗二叉树要么是N0 要么是N1 要么是N2（N0代表度为0的节点个数，N1、N2同理）

所以说我们可以得到N=N0+N1+N2 （1）

我们还需要借助一条性质：一颗有N个节点的树应该有N+1条边

所以说边的总数：

度为0的节点能够产生多少条边？ 0条

度为1的节点能够产生多少条边？1*N1 条

度为2的节点能够产生多少条边？2*N2 条

所以说我们可以得到公式：

N - 1 = 0 + N1 + N2 + N2（2）

N - 1 = N1 + N2 + N2

然后我们套入公式（1）

N0 + N1 + N2 - 1 = N1 + N2 + N2

连边互相抵消

N0 - 1 = N2

N0 = N2 + 1

推导完毕

偶数个节点的树有度数为1的节点

奇数个节点的树没有度数为1的节点

二叉树的存储：顺序存储和链式存储

二叉树的题天生就是用递归来写的（慢慢体会）

二叉树的遍历

先序遍历

力扣原题链接：力扣

二叉树的先序遍历的遍历方式为根->左子树->右子树

当然理解起来是比较抽象的我们还是上图

所以根据以上思路我们写出以下代码即可先序遍历二叉树

public static void preorderTraversal(TreeNode root){
        if(root==null){
            return ;
        }
        System.out.print(root.val+" ");
        preorderTraversal(root.left);
        preorderTraversal(root.right);
    }

力扣题解题

因为力扣题最终要将数据保存到一个链表中我们需要稍微的变更一下思路提供三种解题思路

1.子函数方式

public void _preorderTraversal(TreeNode root,List<Integer> ret){
        if(root==null){
            return ;
        }
        ret.add(root.val);
        _preorderTraversal(root.left,ret);
        _preorderTraversal(root.right,ret);
    }
    
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        _preorderTraversal(root,list);
        return list;
    }

2. 根据前序遍历优化思路版

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>(); 
        if(null==root){
            return list;
        }

        list.add(root.val);
        List<Integer> lefttree=preorderTraversal(root.left);
        list.addAll(lefttree);
        List<Integer> righttree=preorderTraversal(root.right);
        list.addAll(righttree);

        return list;
    }

3.非递归版

 public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list=new ArrayList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;

        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
            list.add(cur.val);
            stack.push(cur);
            cur=cur.left;
        }
            cur=stack.pop().right;
            //cur=cur;
        }
        return list;
    }

中序遍历

力扣原题链接：力扣

二叉树的中序遍历的遍历方式为：左子树-> 根 ->右子树

代码实现：

public static void inorderTraversal(TreeNode root){
        if(root==null){
            return ;
        }
        inorderTraversal(root.left);
        System.out.print(root.val+" ");
        inorderTraversal(root.right);
    }

力扣题解

其实解法还是三种但是因为跟之前思路是差不多的所以只举例一种

 public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list=new LinkedList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.pop();
            list.add(top.val);
            cur=top.right;
        }
        return list;
    }

后序遍历

力扣原题链接：力扣

二叉树的后序遍历顺序为：左子树->右子树->根

代码实现：

    public static void postorderTraversal(TreeNode root){
        if(root==null){
            return ;
        }
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        System.out.print(root.val+" ");
    }

力扣题解：

因为后序遍历的非递归遍历难度较大所以此处放非递归代码

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list=new LinkedList<>();
        Stack<TreeNode> stack=new Stack<>();
        TreeNode cur=root;
        TreeNode prev=null;
        while(cur!=null||!stack.isEmpty()){
            while(cur!=null){
                stack.push(cur);
                cur=cur.left;
            }
            TreeNode top=stack.peek();
            if(top.right==null||top.right==prev){
                list.add(top.val);
                prev=top;
                stack.pop();
            }else{
                cur=top.right;
            }
        }
        return list;
    }

层序遍历

力扣原题链接力扣

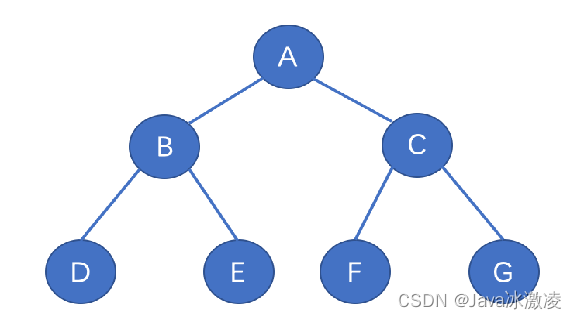
层序遍历就是一层一层遍历例如这个图层序遍历结果为ABCDEFG

力扣题解：

我们如果要进行层序遍历的话需要借助到一个数据结构为队列

1.我们将一个节点的左右子树（如果不为空）则放入队列

2.第二次遍历便继续将每个节点的左右子树放入队列

代码：

 public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> lists = new LinkedList<>();
        if(root==null){
            return lists;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);  
        while(!queue.isEmpty()){
            List<Integer> list = new LinkedList<>();
            lists.add(list);
            int size=queue.size();
            while(size>0&&!queue.isEmpty()){
                TreeNode cur=queue.poll();
                list.add(cur.val);
                if(cur.left!=null){
                    queue.offer(cur.left);
                }
                if(cur.right!=null){
                    queue.offer(cur.right);
                }
                size--;
            }
        }
        return lists;
    }