目录
引言
什么是AVL树?
AVL树也是一颗二叉搜索树,只不过AVL树在二叉搜索树的基础上做了平衡处理。通过平衡因子保证树的平衡。平衡树的高度。
为什么需要AVL树?
二叉搜索树(BST)的查找、插入和删除操作在理想情况下时间复杂度为 O(logn),但若插入数据是有序的(例如依次插入1,2,3,…,n),BST会退化为链表,操作效率降至 O(n)。因为二叉搜索树的效率跟其高度有关,所以为了避免退化成链表,只需对树的高度进行控制就行,而AVL树通过动态调整树的结构,确保树的所有操作的时间复杂度稳定在O(logn)。
一、AVL树的概念
1.平衡因子
AVL树的每个节点都有一个平衡因子,定义为:
- 平衡因子 = 右子树高度 - 左子树高度
AVL树要求所有节点的平衡因子必须为-1,0,1。如果某个节点的平衡因子的绝对值大于1,则说明该树失衡,需要通过旋转操作调整。
结构如下:

二、AVL树的核心操作
2.1、AVL树节点定义
template<class K,class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K,V>* _parent;//该节点父亲
AVLTreeNode<K,V>* _left; //该节点左孩子
AVLTreeNode<K,V>* _right; //该节点右孩子
int _bf; //表示该节点的平衡因子
AVLTreeNode(const pair<K,V>& kv)
:_parent(nullptr)
,_left(nullptr)
,_right(nullptr)
,_kv(kv)
,_bf(0)
{}
};
-
父节点指针:在 AVL 树的插入和删除操作中,需要通过父节点来调整树的结构。例如,在旋转操作中,需要知道当前节点的父节点,以便正确地调整父子关系。
2.2、AVL树的插入
思路:
- 按照二叉搜索树的方式插入新节点。
- 更新平衡因子,判断树是否平衡,需不需要调整。
场景分析:
1、新增节点在左,parent平衡因子减减

2、新增节点在右,parent平衡因子加加

3、更新后parent平衡因子==0,说明parent所在子树的高度不变,不会影响祖先,不用再沿着到root的路径往上更新
4、更新后parent平衡因子==1或-1,说明parent所在子树的高度变化,会影响祖先,需要继续沿着到root的路径往上更新
5、更新后parent平衡因子==2或-2,说明parent所在子树的高度变化且不平衡,对parent所在子树进行旋转,让树平衡

bool insert(const pair<K, V>& kv)
{
//插入新节点操作和二插搜索树一样,这里先不写
//......
//AVL平衡,更新平衡因子
while (parent)
{
if (parent->_right == cur)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == -1 || parent->_bf == 1)
{
//继续向上更新平衡因子
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2)
{
//子树不平衡,需要旋转
// ......
}
else
{
assert(false);
}
}
return true;
}2.2.1、AVL树的旋转分析
旋转的四种情况:
1、新节点插入较高右子树的右侧--左单旋
核心操作:
parent->right = cur->leftcur->left = parent

旋转需要注意的问题:
1、保证旋转完还是搜索树
2、变成平衡树且降低该树高度
左旋代码:
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
// 将原父节点的右子节点指向当前节点的左子节点
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent; // 更新左子节点的父节点为原父节点
}
Node* ppnode = parent->_parent; // 获取原父节点的父节点
cur->_left = parent; // 将原父节点设置为当前节点的左子节点
parent->_parent = cur; // 更新原父节点的父节点为当前节点
// 如果原父节点是根节点,则更新根节点为当前节点
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
// 如果原父节点不是根节点,更新其父节点的相应子节点为当前节点
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
// 更新平衡因子,由于是左旋,原父节点和当前节点的平衡因子都设置为0
parent->_bf = cur->_bf = 0;
}2、新节点插入较高左子树的左侧--右单旋
核心操作:
parent->left = cur->rightcur->right = parent

原理跟上面类似
右单旋代码:
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
// 将原父节点的左子节点指向当前节点的右子节点
parent->_left = curright;
if (curright)
{
curright->_parent = parent; // 更新右子节点的父节点为原父节点
}
Node* ppnode = parent->_parent;
cur->_right = parent; // 将原父节点设置为当前节点的右子节点
parent->_parent = cur; // 更新原父节点的父节点为当前节点
// 如果原父节点是根节点,则更新根节点为当前节点
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
// 更新平衡因子,由于是右旋,原父节点和当前节点的平衡因子都设置为0
parent->_bf = cur->_bf = 0;
}3、新节点插入较高左子树的右侧---左右双旋:先左单旋再右单旋
下面图中的h表示树的高度
在b或c任意位置插入新节点都会导致双旋:
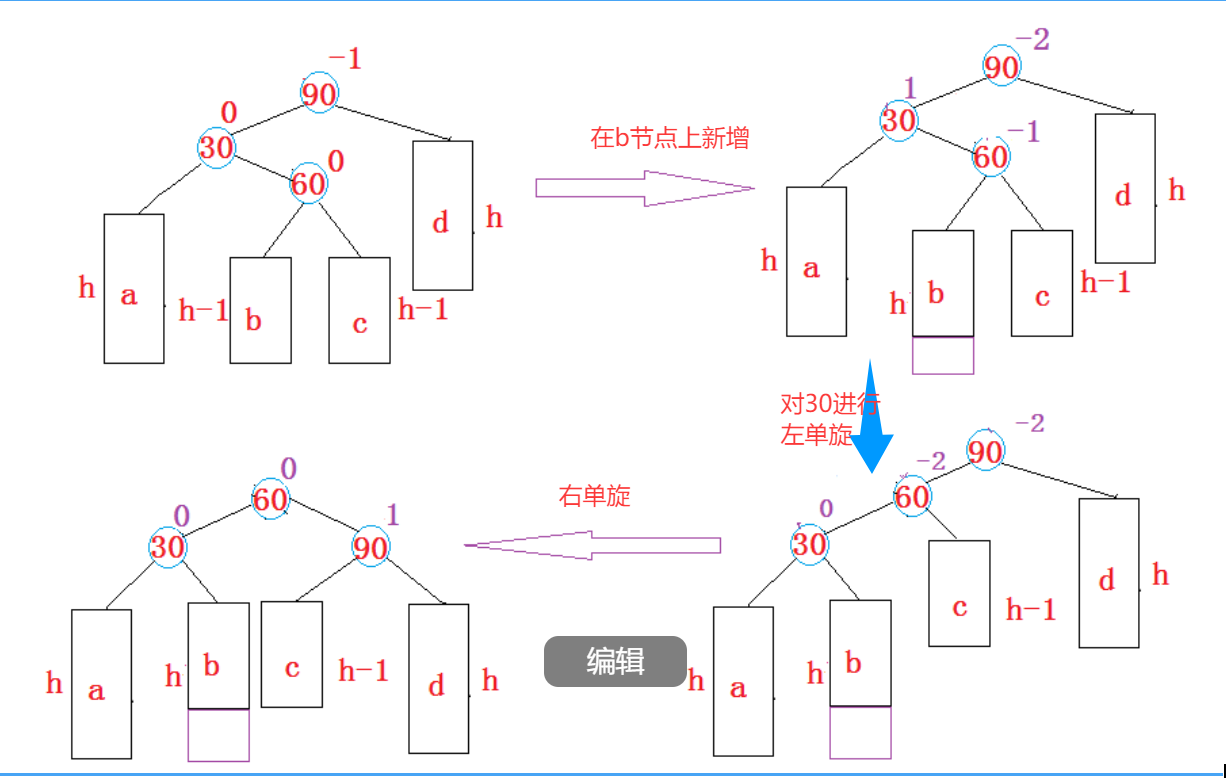
先对30进行左单旋,然后再对90进行右单旋
4、新节点插入较高右子树的左侧---右左双旋:先右单旋再左单旋

2.2.2、双旋平衡因子分析
以此图(左右双旋)为例:

从左右双旋的结果上来看:
60的左边给了30的右边,
60的右边给了90的左边,
60成了这棵树的根
可以看出,最后平衡因子的更新结果跟60这个节点的平衡因子有关。
- 当60的平衡因子==0时,说明60就是新增,最后旋转的结果:30和90的平衡因子==0。
- 当60的平衡因子==-1时,说明在60的左边新增了节点,那么最后旋转的结果肯定会让30右边减少一个节点,30节点的平衡因子就会减一个 (30->bf==0);90节点的左边节点高度就会比右边高度少一个,那么(90->bf==1)。
- 当60的平衡因子==1时,说明新增节点在60的右边,那么最后30节点的右边就少两个节点(30->bf==-1);90节点的左边少两个节点,则(90->bf==0)。
void RotateLR(Node* parent) // 左右双旋
{
Node* cur = parent->_left;
Node* curright = cur->_right;
int bf = curright->_bf; // 保存当前节点右子节点的平衡因子
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curright->_bf = 0;
}
else if (bf == 1)
{
// 如果当前节点的右子节点的平衡因子为1,说明在右子树新增了节点
parent->_bf = 0; // 父节点的平衡因子为0
cur->_bf = -1; // 当前节点的平衡因子为-1(左子树比右子树高)
curright->_bf = 0; // 当前节点的右子节点的平衡因子为0
}
else if (bf == -1)
{
// 如果当前节点的右子节点的平衡因子为-1,说明在左子树新增了节点
parent->_bf = 1; // 父节点的平衡因子为1(右子树比左子树高)
cur->_bf = 0; // 当前节点的平衡因子为0
curright->_bf = 0; // 当前节点的右子节点的平衡因子为0
}
else
{
assert(false); // 如果平衡因子不在[-1, 1]范围内,抛出断言错误
}
}右左双旋的平衡因子跟上面类似。
void RotateRL(Node* parent) // 右左双旋
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
int bf = curleft->_bf; // 保存当前节点左子节点的平衡因子
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curleft->_bf = 0;
}
else if (bf == 1)
{
// 如果当前节点的左子节点的平衡因子为1,说明在右子树新增了节点
parent->_bf = -1; // 父节点的平衡因子为-1(左子树比右子树高)
cur->_bf = 0; // 当前节点的平衡因子为0
curleft->_bf = 0; // 当前节点的左子节点的平衡因子为0
}
else if (bf == -1)
{
// 如果当前节点的左子节点的平衡因子为-1,说明在左子树新增了节点
parent->_bf = 0; // 父节点的平衡因子为0
cur->_bf = 1; // 当前节点的平衡因子为1(右子树比左子树高)
curleft->_bf = 0; // 当前节点的左子节点的平衡因子为0
}
else
{
assert(false); // 如果平衡因子不在[-1, 1]范围内,抛出断言错误
}
}2.3、AVL的删除
AVL节点的删除可以看看这篇
【高阶数据结构】平衡二叉树(AVL)的删除和调整_平衡二叉树删除节点后怎么调整-优快云博客
三、验证AVL树的平衡
// AVL树的验证(平衡因子方向:右子树高度 - 左子树高度)
bool IsAVLTree()
{
return _IsValidBST(_root) && _IsAVLTree(_root);
}
// 验证BST性质
bool _IsValidBST(Node* root, Node* min = nullptr, Node* max = nullptr)
{
if (root == nullptr) return true;
if ((min && root->key <= min->key) || (max && root->key >= max->key))
{
return false;
}
return _IsValidBST(root->left, min, root) &&
_IsValidBST(root->right, root, max);
}
// 递归验证平衡因子和高度
bool _IsAVLTree(Node* pRoot)
{
if (pRoot == nullptr)
{
return true;
}
// 计算平衡因子(右减左)
int rightH = _Height(pRoot->_right);
int leftH = _Height(pRoot->_left);
int bf = rightH - leftH;
// 检查平衡因子是否合法
if (bf != pRoot->_bf || bf < -1 || bf > 1)
{
return false;
}
// 递归检查子树
return _IsAVLTree(pRoot->_left) && _IsAVLTree(pRoot->_right);
}
// 高度计算(空节点高度为0)
int _Height(Node* pRoot)
{
if (pRoot == nullptr)
{
return 0;
}
return 1 + std::max(_Height(pRoot->_left), _Height(pRoot->_right));
}四、完整代码
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
pair<K, V> _kv;
AVLTreeNode<K,V>* _parent;
AVLTreeNode<K,V>* _left;
AVLTreeNode<K,V>* _right;
int _bf;//表示该节点的平衡因子
AVLTreeNode(const pair<K,V>& kv)
:_parent(nullptr)
,_left(nullptr)
,_right(nullptr)
,_kv(kv)
,_bf(0)
{}
};
template<class K,class V>
class AVLTree
{
typedef AVLTreeNode<K,V> Node;
public:
bool insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//AVL平衡,更新平衡因子
while (parent)
{
if (parent->_right == cur)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == -1 || parent->_bf == 1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == -2 || parent->_bf == 2)
{
//子树不平衡,需要旋转
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
break;
}
else
{
assert(false);
}
}
return true;
}
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
Node* ppnode = parent->_parent;
cur->_left = parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
parent->_bf = cur->_bf = 0;
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
parent->_left = curright;
if (curright)
{
curright->_parent = parent;
}
Node* ppnode = parent->_parent;
cur->_right = parent;
parent->_parent = cur;
if (_root == parent)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
parent->_bf = cur->_bf = 0;
}
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
int bf = curleft->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curleft->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = -1;
cur->_bf = 0;
curleft->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 0;
cur->_bf = 1;
curleft->_bf = 0;
}
else
{
assert(false);
}
}
void RotateLR(Node* parent)
{
Node* cur = parent->_left;
Node* curright = cur->_right;
int bf = curright->_bf;
RotateL(parent->_left);
RotateR(parent);
if (bf == 0)
{
parent->_bf = 0;
cur->_bf = 0;
curright->_bf = 0;
}
else if (bf == 1)
{
parent->_bf = 0;
cur->_bf = -1;
curright->_bf = 0;
}
else if (bf == -1)
{
parent->_bf = 1;
cur->_bf = 0;
curright->_bf = 0;
}
else
{
assert(false);
}
}
void Print()
{
_Print(_root);
}
void _Print(Node* root)
{
if (root == nullptr)
{
return;
}
_Print(root->_left);
cout << root->_kv.first << " ";
_Print(root->_right);
}
// AVL树的验证
bool IsAVLTree()
{
return _IsAVLTree(_root);
}
// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAVLTree(Node* pRoot)
{
if (pRoot == nullptr)
{
return true;
}
int h = _Height(pRoot->_right) - _Height(pRoot->_left);
if (h != pRoot->_bf || h > 1 || h < -1)
{
return false;
}
return _IsAVLTree(pRoot->_left) && _IsAVLTree(pRoot->_right);
}
size_t _Height(Node* pRoot)
{
if (pRoot == nullptr)
{
return 0;
}
int leftH = _Height(pRoot->_left);
int rightH = _Height(pRoot->_right);
return leftH > rightH ? leftH + 1 : rightH + 1;
}
private:
Node* _root = nullptr;
};




















 1076
1076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








