【双指针】

有趣的中国人

已于 2024-04-22 15:28:48 修改

阅读量706

点赞数 18

分类专栏：经典算法文章标签： leetcode 算法职场和发展

于 2024-04-18 23:28:30 首次发布

本文链接：https://blog.youkuaiyun.com/m0_68617301/article/details/137906500

版权

经典算法专栏收录该内容

1 篇文章

订阅专栏

2. LeetCode 1089. 复写零

4. LeetCode 11. 盛水最多的容器

4.1 题目描述

4.2 题目思路

4.3 实现代码

5. LeetCode 611. 有效三角形的个数

5.1 题目描述

5.2 题目思路

5.3 实现代码

6. LeetCode LCR 179.查找总价格为目标值的两个商品

1. LeetCode 283. 移动零

1.1 题目描述

题目链接：

LeetCode 283. 移动零https://leetcode.cn/problems/move-zeroes/description/

1.2 题目思路

题目要求，将数字零移动到数组最后，并不影响非零元素的相对位置，

我们可以利用两个指针dest和cur，cur用来遍历数组，dest用来指向非零元素的最后一个位置；
要保证[0, dest] 的元素是非零元素，[dest + 1, cur - 1] 的元素是全零，[cur , size() - 1]是未处理过的元素;
那我们只需看一下cur指向的元素是否是零，如果是零，就++cur，否则就交换dest和cur所在位置的值即可，然后再++cur，++dest。

1.3 实现代码

class Solution 
{
public:
    void moveZeroes(vector<int>& nums) 
    {
        int dest = -1, cur = 0;
        while(cur < nums.size())
        {
            if (nums[cur] != 0) 
            {
                ++dest;
                swap(nums[cur],nums[dest]);
            }
            ++cur;
        }
    }
};

2. LeetCode 1089. 复写零

2.1 题目描述

题目链接：

LeetCode 1089. 复写零https://leetcode.cn/problems/duplicate-zeros/

2.2 题目思路

这题依然是定义两个指针，cur和dest，cur用来遍历数组，如果dest从前往后覆盖，肯定会把还未处理的值覆盖，所以dest只能从后往前覆盖，那我们肯定要找到最后一个要覆盖的值的位置，那如何找到呢：

如果cur所在位置的值为零，那dest就往后走两步；
否则dest往后走一步，每次走完都要判断dest所在的位置是否大于了size()；
然后再++cur；
最后cur所在位置就是最后一个要复写的值。

这里需要有一个细节判断，当最后一个要复写的位置是零，并且如果dest向后走两步的话就超过了size()，这个时候应该：

--dest，然后让dest所在位置的值赋为0；
--cur。

OK，这样就可以从后往前开始复写了：

如果cur所在位置的值不为零，就把这个位置的值赋给dest所在的位置；
然后--cur，--dest，直到cur < 0。

2.3 实现代码

class Solution 
{
public:
    void duplicateZeros(vector<int>& arr) 
    {
        int cur = 0, dest = -1;
        // 找到最后一个数
        while (cur <  arr.size())
        {
            if (arr[cur] != 0) 
            { 
                ++dest;
            }
            else
            {
                dest += 2;
            }
            if (dest >= arr.size() - 1) break;
            ++cur;
        }
        // 判断边界
        if (dest == arr.size())
        {
            --dest;
            arr[dest] = 0;
            --dest;
            --cur;
        }
        // 从后往前复写
        while (cur >= 0)
        {
            if (arr[cur])
            {
                arr[dest] = arr[cur];
                --dest; 
                --cur;
            }
            else
            {
                arr[dest - 1] = arr[dest] = arr[cur];
                --cur; 
                dest -= 2;
            }
        }
    }
};

3. LeetCode 202. 快乐数

3.1 题目描述

LeetCode 202. 快乐数https://leetcode.cn/problems/happy-number/

3.2 题目思路

对于这道数字变换的题目，怎么能用到双指针呢？

其实这里的双指针，并不是实际意义上的指针，听我细细道来：

这道题有一个点非常重要，题目说经过不停地变换，最后要么是无限循环，要么是变为1，其实变为1之后也是无限循环；
那我么就可以运用这个规律来实现，定义一个slow，每次变换一次，fast，每次变换两次，那么最后fast和slow肯定相等，相等之后退出循环；
最后如果slow和fast变成了1，那么就是快乐书，否则不是。

3.3 实现代码

class Solution 
{
public:
    int changeNum(int n)
    {
        int sum = 0;
        while (n)
        {
            sum += (n % 10) * (n % 10);
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) 
    {
        int slow = n, fast = changeNum(n);
        while (slow != fast)
        {
            slow = changeNum(slow);
            fast = changeNum(fast);
            fast = changeNum(fast);
        }
        if (slow == 1) return true;
        return false;
    }
};

4. LeetCode 11. 盛水最多的容器

4.1 题目描述

题目链接

11. 盛最多水的容器 - 力扣（LeetCode）https://leetcode.cn/problems/container-with-most-water/description/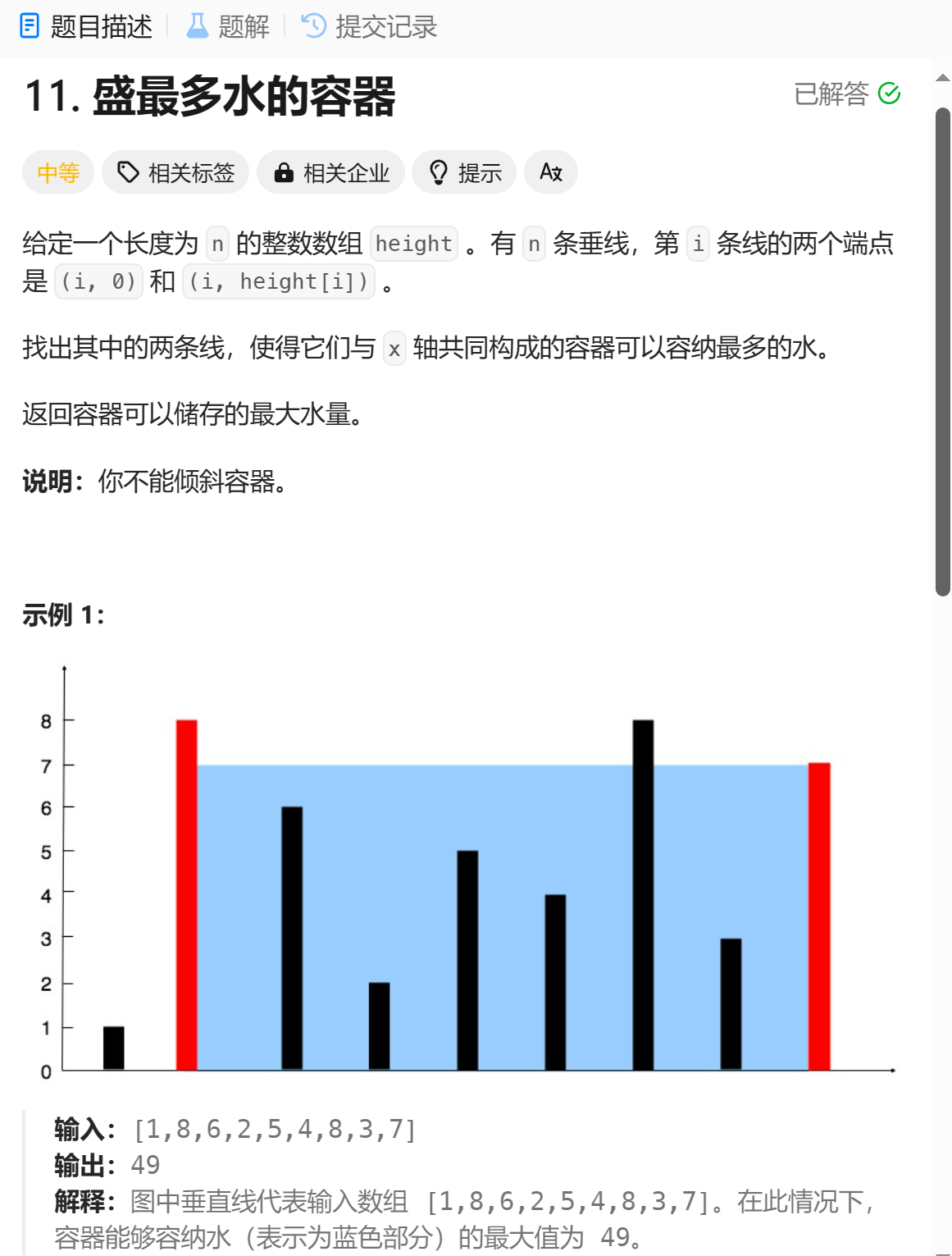

4.2 题目思路

方法一：

这题暴力解法思路很简单，就是把每个面积都求出来，取最小的就行，很明显时间复杂度是O(N^2)，就不多讲了。

方法二：

定义两个指针left和right，left指向数组的开头位置，right指向数组的最后一个元素位置；
算出此时的面积square；
因为square = height * width，他的高度是由较小的那个决定的，如果left所在位置的值小，如果right向前走，height不会变，但是width肯定会变小，所以面积肯定是会变小的，此时就不用多余的计算面积了，直接让left--；
同理如果right所在位置的值小，那么如果让left++，那么height不会变，但是width肯定会变小，所以面积肯定会减小，这个时候--right即可。
直至left与right相遇。

那么这个算法的时间复杂度是left和right便利了一边数组，时间复杂度是O(N)；

4.3 实现代码

class Solution 
{
public:
    int _Square(int width, int height)
    {
        return width * height;
    }
    int maxArea(vector<int>& height) 
    {
        int left = 0;
        int right = height.size() - 1;
        int Square = 0;
        while (left < right)
        {
            int tmpSquare = _Square(right - left, min(height[right],height[left]));
            if (tmpSquare > Square) Square = tmpSquare;
            if (height[right] < height[left]) --right;
            else ++left;
        }
        return Square;
    }
};

5. LeetCode 611. 有效三角形的个数

5.1 题目描述

题目链接

611. 有效三角形的个数 - 力扣（LeetCode）https://leetcode.cn/problems/valid-triangle-number/

5.2 题目思路

方法一：

这题暴力解法就是把数组中取三个数的情况都列举出来，并判断是否能构成三角形，但是三角形要满足任意两边之和大于第三边，因此要判断三次，但是我们只要知道最大的边是哪一条，就可以判断一次，因此排序可以简化判断次数，但是这样的时间复杂度还是很高。

方法二：

既然数组必然要进行排序，那么数组肯定是有序了，既然有序了，我们可以思考一下更简单的方法。

既然要判断两个较小值的和是否大于最大的数，我们可以从后向前固定最大数；
然后定义left = 0，right为最大数位置的前一个位置；
判断两个位置的值是否大于最大的数，如果大于，那么说明[left, right - 1]区间内所有的值都能与 right 和固定的最大数组成三角形，然后--right；
如果不大于，就让left++；
直至left与right相遇。

5.3 实现代码

class Solution 
{
public:
    int triangleNumber(vector<int>& nums) 
    {
        int ret = 0;
        int n = nums.size();
        int loc = n - 1;
        sort(nums.begin(),nums.end());
        while (loc > 0)
        {
            int left = 0, right = loc - 1;
            while (left < right)
            {
                // 判断较小的两边之和是否大于最大边
                if (nums[left] + nums[right] > nums[loc])
                {
                    ret += (right - left);
                    --right;
                }
                else
                {
                    ++left;
                }
            }
            --loc;
        }
        return ret;


    }
};

6. LeetCode LCR 179.查找总价格为目标值的两个商品

6.1 题目描述

题目链接

LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/description/

6.2 题目思路

这题暴力解法思路也很简单，就是计算所有的两数之和即可。很明显时间复杂度O(N^2)。

除此之外，我们可以利用排序+单调性来做：

首先对数组进行排序；
定义两个指针left和right分别指向第一个元素和最后一个元素所在的位置；
判断此时两个位置的和是否==target；
如果大于就--right，小于就++left，等于就返回。

6.3 实现代码

class Solution 
{
public:
    vector<int> twoSum(vector<int>& price, int target) 
    {
        sort(price.begin(),price.end());
        int left = 0, right = price.size() - 1;
        while (left < right)
        {
            if (price[left] + price[right] > target) --right;
            else if (price[left] + price[right] < target) ++left;
            else return {price[left],price[right]};
        }
        return {0,0};
    }
};

7. LeetCode 15. 三数之和

7.1 题目描述

题目链接

15. 三数之和 - 力扣（LeetCode）https://leetcode.cn/problems/3sum/description/

7.2 题目思路

这题与两数之和较为类似，与两数之和稍微不同的是，题⽬中要求找到所有「不重复」的三元组。那我们可以利⽤在两数之和
那⾥⽤的双指针思想，来对我们的暴力枚举做优化：

先排序；
然后固定⼀个数a ：
在这个数后⾯的区间内，使⽤「双指针算法」快速找到两个数之和等于a即可。

但是要注意的是，这道题⾥⾯需要有「去重」操作

找到⼀个结果之后， left 和right指针要「跳过重复」的元素；
当使⽤完⼀次双指针算法之后，固定的 a 也要「跳过重复」的元素

7.3 实现代码

class Solution 
{
public:
    vector<vector<int>> threeSum(vector<int>& nums) 
    {
        vector<vector<int>> vv;
        sort(nums.begin(),nums.end());
        for (int i = 0;i <= nums.size() - 3; ++i)
        {
            if (nums[i] > 0)
            {
                break;
            }
            int left = i + 1;
            int right = nums.size() - 1;
            while (left < right)
            {
                if (nums[left] + nums[right] + nums[i] < 0) ++left;
                else if (nums[left] + nums[right] + nums[i] > 0) --right;
                else 
                {
                    vv.push_back({nums[left],nums[right],nums[i]});
                    while (left < right && nums[left] == nums[left + 1]) 
                    {
                        ++left;
                    }
                    ++left;
                    while (left < right && nums[right] == nums[right - 1]) 
                    {
                        --right;
                    }
                    --right;
                }
            }
            while (i < nums.size() - 3 && nums[i] == nums[i + 1])
            {
                ++i;
            }
        }
        return vv;
    }
};

8. LeetCode 18. 四数之和

8.1 题目描述

题目链接

18. 四数之和 - 力扣（LeetCode）https://leetcode.cn/problems/4sum/description/

8.2 题目思路

这题和三数之和也很类似，首先固定一个数，然后利用三数之和的思想。

8.3 实现代码

class Solution 
{
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) 
    {
        vector<vector<int>> vv;
        sort(nums.begin(), nums.end());
        if (nums.size() < 4) return vv;
        for (int i = 0;i <= nums.size() - 4; ++i)
        {
            for (int j = i + 1; j <= nums.size() - 3; ++j)
            {
                int left = j + 1, right = nums.size() - 1;
                while (left < right)
                {
                    if ((long long)nums[i] + nums[j] + nums[left] + nums[right] < target)
                    {
                        ++left;
                    }
                    else if ((long long)nums[i] + nums[j] + nums[left] + nums[right] > target)
                    {
                        --right;
                    }
                    else
                    {
                        vv.push_back({nums[i],nums[j],nums[left],nums[right]});
                        while (left < right && nums[left] == nums[left + 1])
                        {
                            ++left;
                        }
                        ++left;
                        while (left < right && nums[right] == nums[right - 1])
                        {
                            --right;
                        }
                        --right;
                    }
                }
                while (j < nums.size() - 3 && nums[j] == nums[j + 1])
                {
                    ++j;
                }
            }
            while (i < nums.size() - 4 && nums[i] == nums[i + 1])
            {
                ++i;
            }
        }
        return vv;

    }
};