非线性结构——树（一）

目录

 

 一、树

1、树的定义

2、树的术语

3、树的基本运算

二、二叉树

1、二叉树定义

2、二叉树的性质

3、二叉树的存储

3.1、顺序存储

3.2、链式存储

3.2.1二叉链表存储

 3.2.2三叉链表存储

---

 一、树

1、树的定义

树是n个结点的集合，n=0是为空树，

n>0时，树需满足两个条件：

1、有且仅有一个根节点。

2、除根节点以外的n-1个结点划分为m个互不相交的T1、T2、Tm的有限集合，每个Tm又是一个子树。每颗子树的根节点有且仅有一个直接前驱，

2、树的术语

用一个例图更好理解：

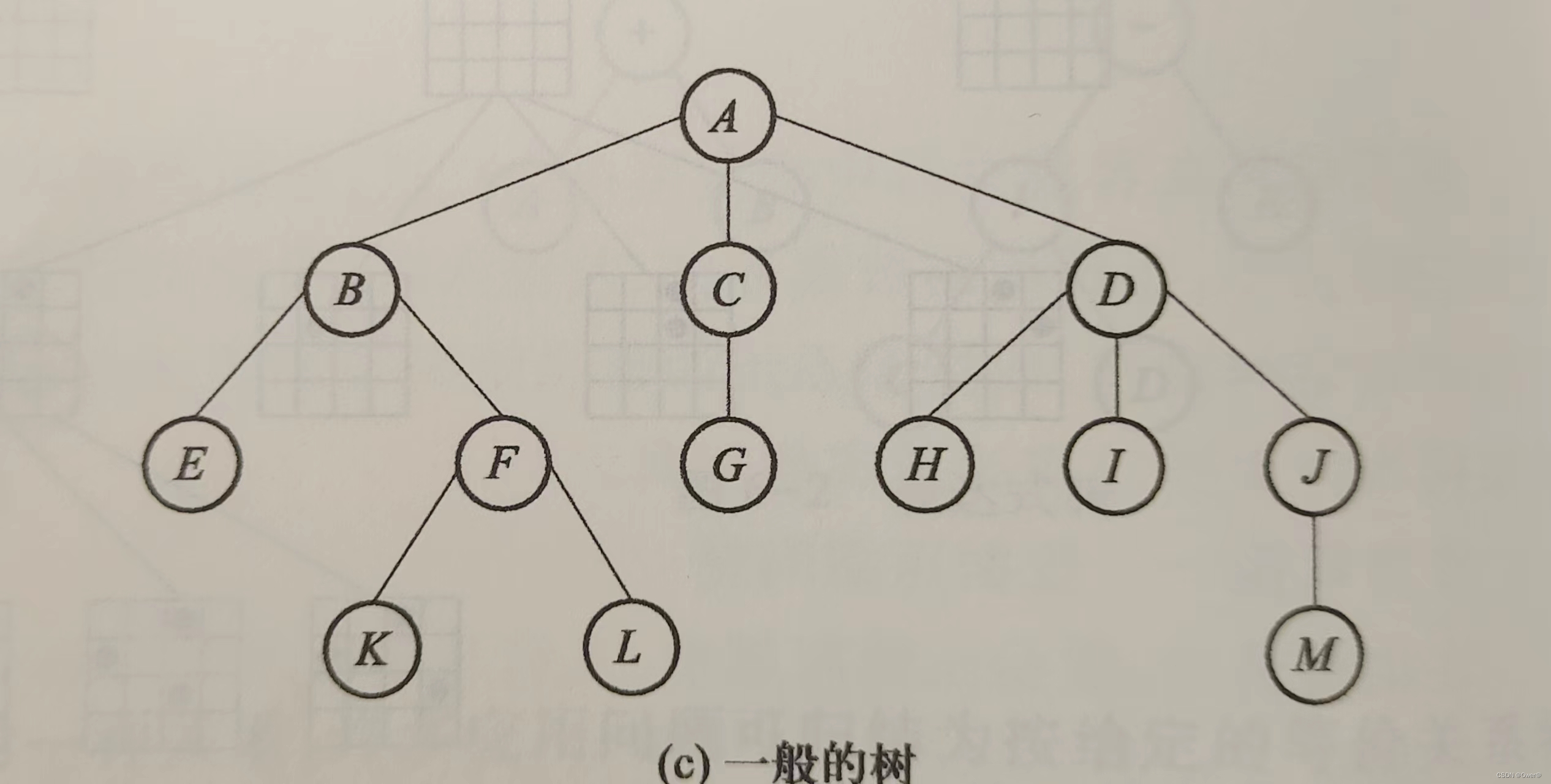
（1）结点：包含一个数据元素，及若干指向子树的分支，图：树总共有13个结点

（2）结点的度：结点拥有子树的个数。图中A的度为3

（3）树的度：树中所有结点度的最大值。图中树的度为3.

（4）叶子结点：度为0的结点为叶子结点，也为终端结点。kLM均为叶子结点。

（5）内部结点：度不为0的结点。

  借助人类族谱的术语描述

（6）孩子结点：结点的直接后继为孩子结点，如：B、C、D为根节点的孩子结点。

（7）双亲节点：结点是子树根的双亲，A是B、C、D的双亲，D是HIJ的双亲

（8）兄弟结点：同一双亲的孩子结点之间互称。H、I、J互为兄弟结点。

（9）堂兄弟：双亲是兄弟的或堂兄弟的结点之间互称。如：E、G、H的双亲是兄弟，互为堂兄弟结点、LM的双亲FJ互为堂兄弟，其LM互为堂兄弟结点。

（10）祖先结点：指从根节点到该结点的路径上的所有结点。结点K的祖先结点为F、B、A结点。

（11）子孙结点：指该结点子树中的所有结点。如：D的子孙结点为：H、I、J、M。

（12）结点的层次：根节点为第一层、根的孩子为第二层依次类推

（13）根的深度：树的所有结点层次的最大值，图中树的深度（高度）为4。

（14）森林：m（m>=0）课互不相交的树的集合。

（15）有序树与无序树：树中结点的各课子树的从左到右特定次序的为有序树。

3、树的基本运算

（1）结点赋值：Assign(Tree,x,v) ，x是树中的某个结点，将v的值赋给x结点

  (2)插入操作：InsertChild(Tree,p,Child),p指向树中的某个结点，非空树Child与树Tree互不相交，将Child插入到p所指向的子树中。

（3）删除操作：DeleteChild(Tree,p,i),p指向树中的某个结点，删除p所指向的第 i 颗子树（1=<i<=d,d为p结点的度）

（4）遍历操作：TraverseTree（Tree，Visit（）），Visit（）是对结点进行访问的函数。按照某种次序对树中的每个节点进行访问，且只访问一次，一旦Visit（）失败，则操作失败。

二、二叉树

1、二叉树定义

二叉树是n个结点的有限集合。n=0时，成为二叉树。n>0时，该集合由一个根节点及两颗互不相交的（左子树，右子树）二叉树组成。

二叉树需满足的条件：

（1）每个结点的度不大于2。

（2）每颗子树的位置是明确的，不能改变。

2、二叉树的性质

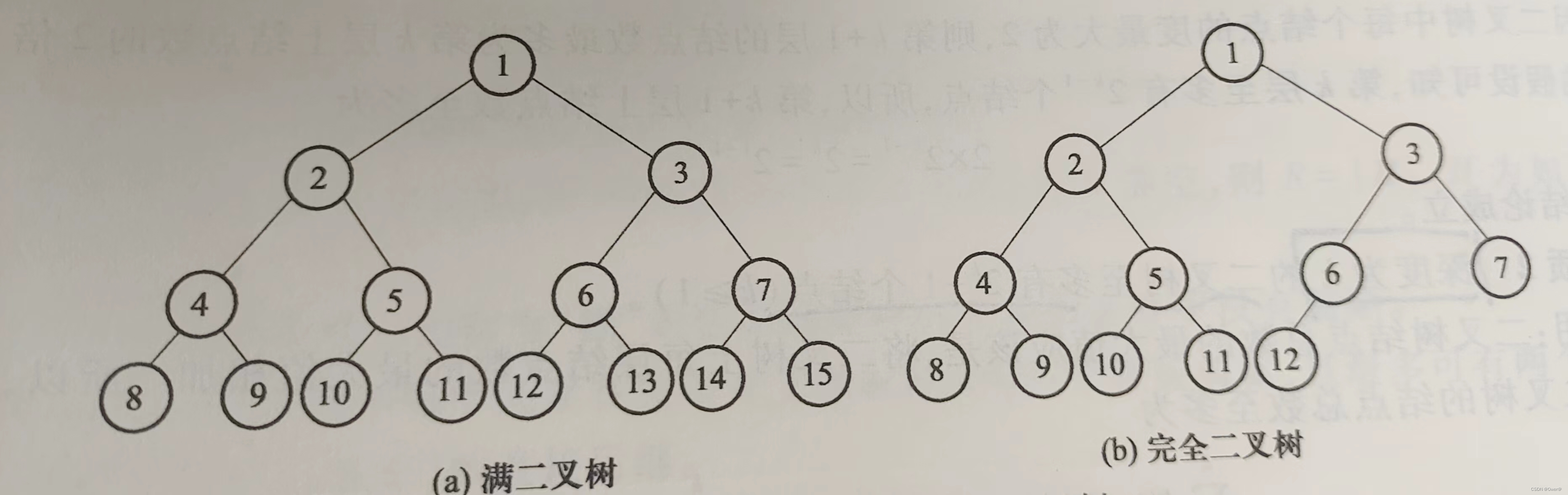
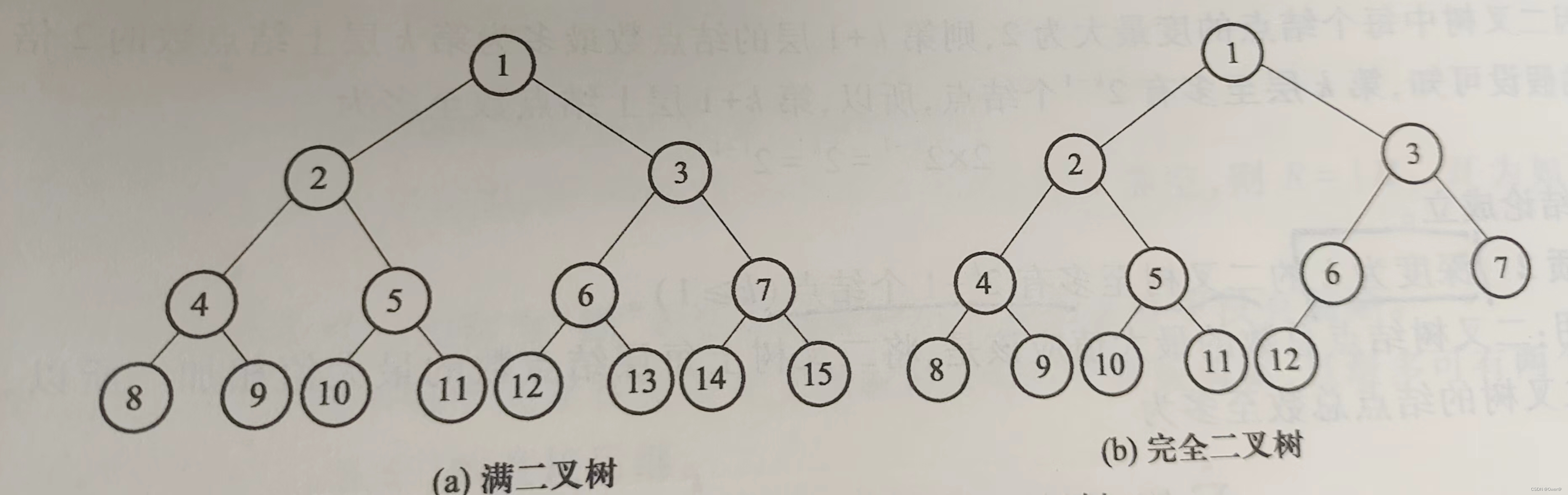
介绍两种特殊的二叉树：（满二叉树与完全二叉树）

满二叉树：深度为k，含有2^k-1个结点的二叉树，每个层次的结点都是满的

完全二叉树：深度为k，含有n（n<=2^k-1）个结点的二叉树，当且仅当n个结点与满叉树中连续编号1-n的结点位置一一对应时为完全二叉树。

完全二叉树的特征：

1、所有叶子结点只可能出现在层号最大的两层上

2、若右子树的层高为k，则左子树的层高为k+1或k。

满二叉树一定是完全二叉树，而二叉树不是满二叉树。

 二叉树的性质：

1、二叉树的第i层上最多有2^(i-1)个结点，i>=1.

2、深度为k的二叉树至多有2^k-1个结点  ，k>=1

3、对任意一颗二叉树T,若终端结点数为n0，度为2的结点数为n2，则n0=n2+1.

4、对于具有n个结点的完全二叉树，如果按照对满二叉树进行连续编号的方式，对所有结点从1开始顺序编号，对任意序号为i的结点有以下结论：

（1）如果i=1，则结点i为根，无双亲结点，i>=1时，结点为 i 的双亲结点序号为【i/2】.

（2）如果2i<=n,则结点i的左孩子结点序号为2i，否则，结点i没有左孩子。

（3）如果2i+1<=n,则结点i的右孩子结点序号为2i+1，否则，结点i没有右孩子。

3、二叉树的存储

二叉树存储分为顺序存储和链式存储，在实际操作中要根据二叉树的形态和操作要求选择不同的存储结构。

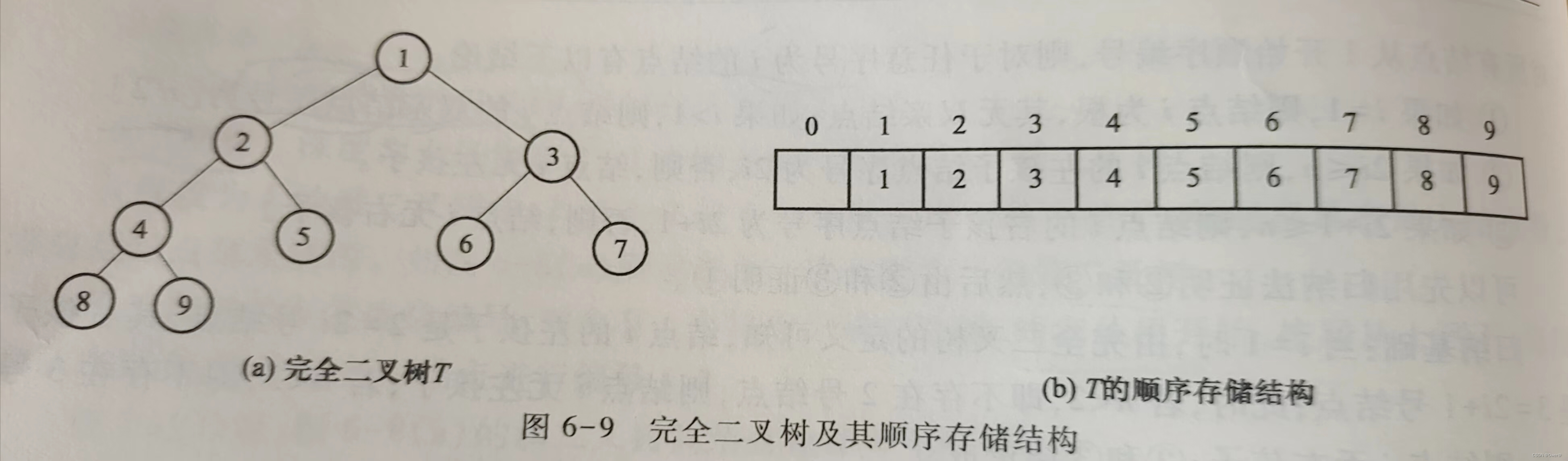
3.1、顺序存储

满二叉树和完全二叉树中各结点是按照1——n连续编号的次序，可按照此次序依次存储到一组连续的存储单元，即用一组一维数组存放。结点i的标号按照i的分量存储到数组中，根据性质知：

i结点的双亲结点为[i/2]，左孩子结点为2i，右孩子结点为2i+1，数组中下标相同。

如图：

 But：

对于一般二叉树来说，各结点无规律连接时，不能将结点连续存储到一维数组中，无法体现结点之间逻辑关系。只能通过补空结点存储，这样虽然一般二叉树只有k个结点，却要2^k个存储单元，造成空间的浪费。

如图：

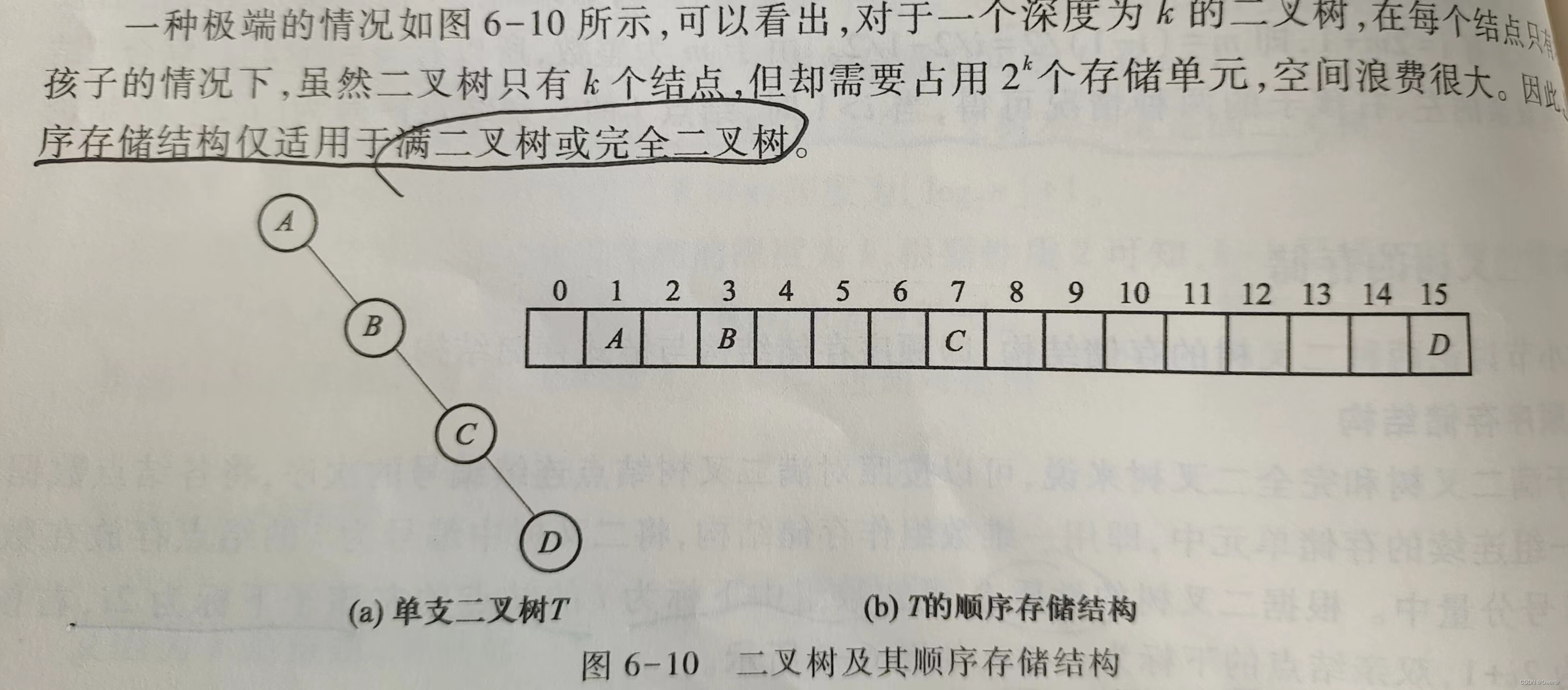
因此：二叉树的顺序存储只适用于满二叉树和完全二叉树。

3.2、链式存储

3.2.1二叉链表存储

对于任意的二叉树，每个结点最多只有两个孩子，每个结点可以设计三个域：数据域、左孩子域、右孩子域。二叉树中有n个结点，则指针域为2n个，其中n-1个指向孩子，n+1个指向空域。

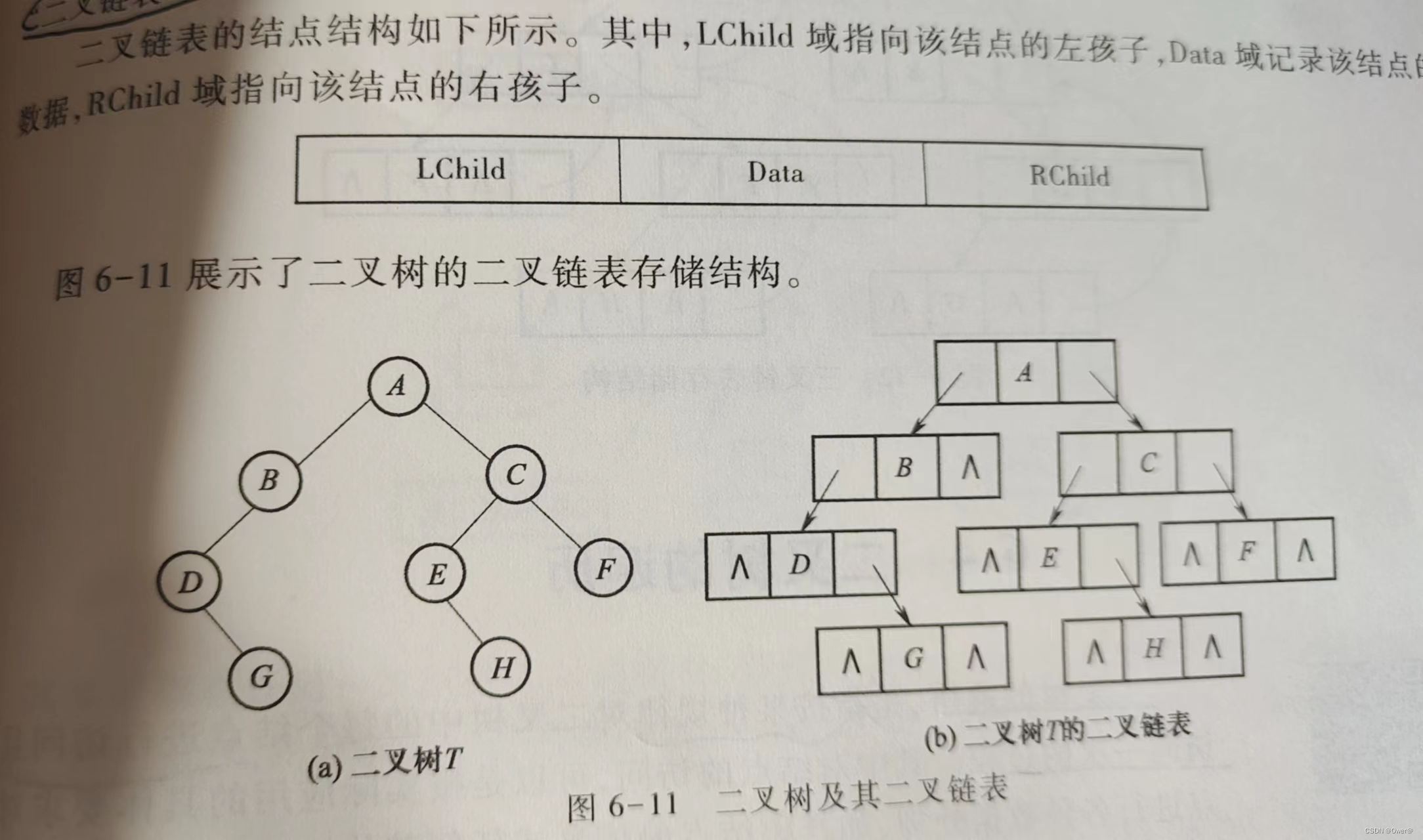
 二叉链表结点结构描述：

typedef struct Node
{
   DataType Node;
   struct Node*Lchild;
   struct Node*Rchild;
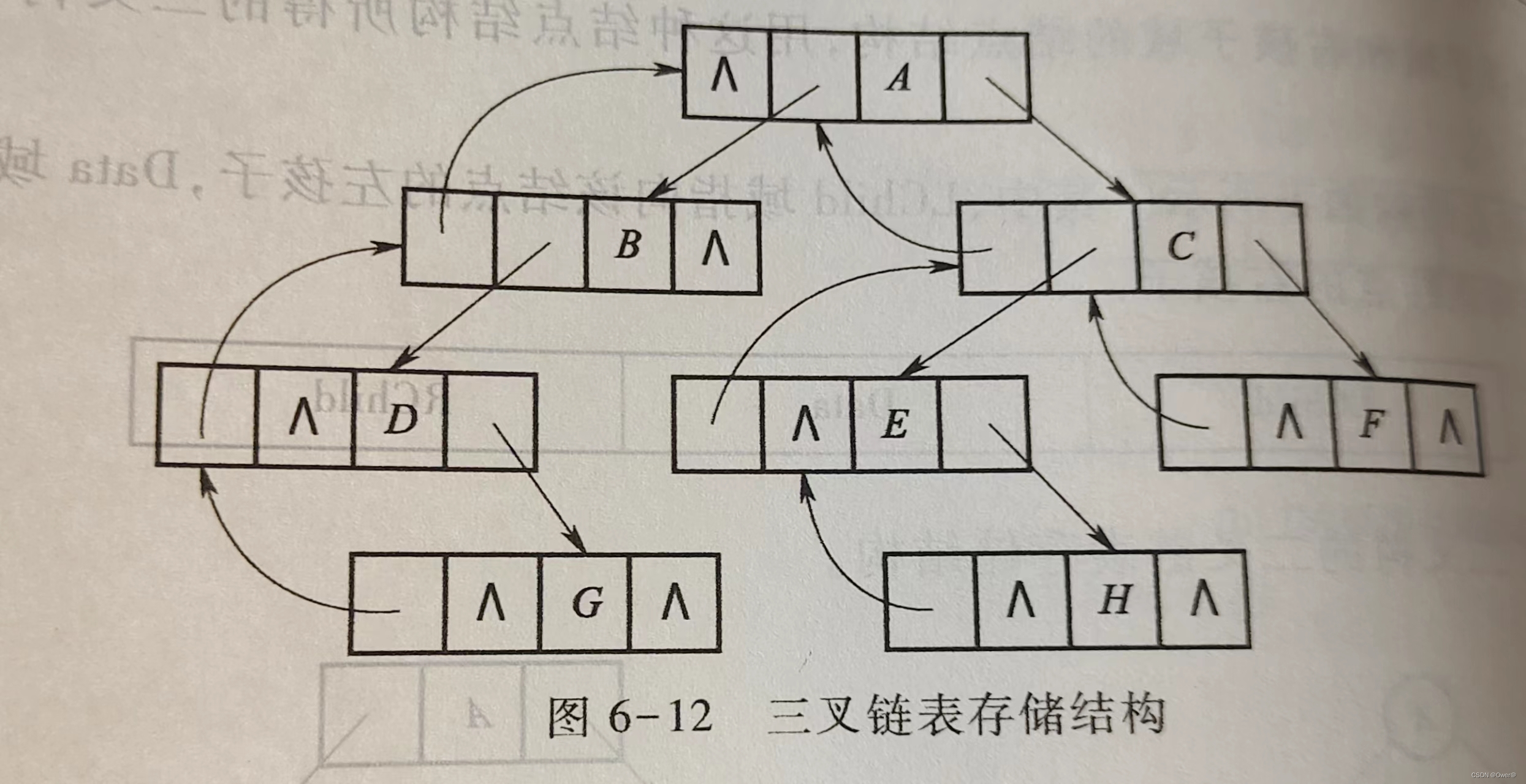
}BiTNode,*BiTree;

 3.2.2三叉链表存储

为了方便找到双亲结点，可以在结构中再设计一个指向双亲结点的域。