机器学习 Logistic回归

Cpigpig

已于 2024-01-01 15:23:13 修改

阅读量886

点赞数 17

分类专栏：机器学习文章标签：机器学习回归人工智能

于 2023-12-02 15:33:16 首次发布

本文链接：https://blog.youkuaiyun.com/m0_67703565/article/details/134743520

版权

机器学习专栏收录该内容

6 篇文章

订阅专栏

本文介绍了logistic回归的基本概念，如何将其用于分类问题，以及算法背后的原理，包括损失函数的选择（如极大似然估计），梯度上升法和梯度下降法的应用，以及随机梯度上升法的改进。通过实例演示了这些方法在实际问题中的应用，如马尔可夫链蒙特卡洛方法和horseColic数据集的测试。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、基本介绍

1. 概念

logistic回归是一种广义的线性回归，与多重线性回归不同的是多重线性回归的因变量是w'x+b，而logistic回归通过函数L将w'x+b对应一个隐状态p=L(w‘x+b)，它在机器学习通常用来解决二分类的问题，也可以解决多分类问题，但是需要使用softmax方法处理。

2. 分类问题

假设我们给出一个的身高判断他是高还是矮，那么这种有序的关系我们把它转化为连续值[0,1]，设定一个阈值x，高于x的就算高，低于x的就算低。

如果是无序关系的话，例如说有3个属性值，分别是色泽、根蒂、敲声，这时我们需要把属性值转换成3维的向量{(0,0,1),(0,1,0),(1,0,0)}。

3. 线性模型的一般形式

$y = g^{-1}(w^{T}x+b)$

g(●)该函数一般是单调可微函数，也被称为联系函数。

比如说对数线性回归是g(●)=ln(●)时广义/多维线性模型的特例。

$\ln y = wx + b$

二、算法原理

假设我们处理一个二分类问题，我们让其中一类标签为0，另一类标签为1.我们需要寻找函数将分类标记与线性回归模型的输出联系起来，第一个想到的就是单位阶跃函数，它的图像如下：

单位阶跃函数：

我们可以看出该函数既不连续也不可微，所以不行。

那么这时候我们又想到了sigmoid函数也被称为逻辑斯蒂函数，它的图像如下：

它是连续的，我们通过sigmoid函数将 $y = \frac{1}{1+e^{-z}}$ 变成 $y = \frac{1}{1+e^{-(w^{T}+b)}}$

三、损失函数

1. 极大似然估计

● 确定待求解的位置参数θ1、θ2，. . . ，比如说均值、方差或者待定分布函数的参数。

● 计算每个样本X1, X2, . . . , Xn的概率密度 f (Xi; θ1, . . . , θm)

● 假定样本i，可以根据样本的概率密度累乘构造似然函数：

L(θ1,.....,θm) = Πf(xi; θ1,.....,θm).

● 通过似然函数最大化(求导为零)，求解未知参数θ(为了降低计算的难度，通常可以采用对数加法替换概率乘法，通过导数为零/极大值来求解未知参数)。

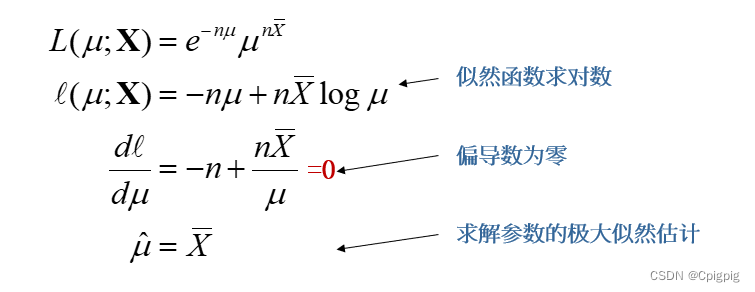
● 假设有样本集{X1,X2,...,Xn}服从参数为μ的泊松分布，对于观测样本的X的概率为：

● 假定样本之间独立同分布，则样本集的联合概率为：

然后对似然函数求对数，转换成加法运算，进而通过偏导数为零求极值，解算待求解参数μ：

四、最佳回归系数的确定

2.梯度上升法

2.1 思想

要找到某个函数的最大值，最好的方法是沿着该函数的梯度方向探寻。

如果梯度记为▽，则函数f(x,y)的梯度就由下列式子表示：

▽f(x,y) = δf(x,y)/δx和δf(x,y)/δy，分别表示沿着x的方向移动和沿着y的方向移动，并且函数f(x,y)要在待计算的点上有定义并且可微。

梯度上升算法的公式为：

w:=w+α▽f(w)

其中w表示模型参数,f(w)表示目标函数,▽f(w)表示目标函数的梯度，α表示学习率，α控制着每一步的步长。

2.2 测试

接下来我们写个测试梯度上升算法，看是如何迭代的：

首先我们假定一个函数 $f(x) = -8x^{2} + 16x$ ,那我们在高中的时候求这个函数的最大值做法是求导，该函数的导数为 $-16x + 16$ ，然后令该导数为0，解出x=1的时候该函数有最大值8.

那我们利用梯度上升法的思想，首先求出该函数的导数，设x_new的初始值为0从0开始迭代，x_old为-1小于x_new。

def f(x):
        return -16*x+16

def Gradient_Ascent_test():
    
    x_old = -1
    x_new = 0
    a = 0.1 #步长
    presision = 0.000000001
    while abs(x_new - x_old) > presision:
        x_old = x_new
        x_new = x_old + a*f(x_old)
        print(x_new)
    print("最终结果")
    print(x_new)

Gradient_Ascent_test()

我们可以看到在不断的更新梯度下，最终的结果的近似值等于1.

2.3案例

使用梯度上升法进行逻辑回归的代码。它包括了从文件中加载数据集、计算 Sigmoid 函数、执行梯度上升以及绘制数据集最佳拟合线的函数。loadSet 函数从文件中读取数据集，并将数据和标签作为列表返回。sigmoid 函数使用 math 模块的 exp 函数来计算给定输入的 Sigmoid 函数值。gradAscent 函数实现了梯度上升算法，以找到逻辑回归模型的最优权重。plotBestFit 函数使用计算出的权重来绘制数据集的最佳拟合线和数据点。它使用 matplotlib 库创建绘图。

from math import exp

import numpy as np


def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('testSet.txt')  
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    fr.close()
    return dataMat, labelMat

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

from matplotlib import pyplot as plt


def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataMat)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]
    ax.plot(x, y)
    plt.title('BestFit')
    plt.xlabel('X1'); plt.ylabel('X2')
    plt.show()

3. 梯度下降法

3.1 思想

我们最经常听的算法应该是和上面的梯度上升法相反的梯度下降法，它们之间的区别是梯度上升用来求函数的最大值，而梯度下降法用来求函数的最小值，也就是将公式中的加法改成减法就行了。

那么我们也来测试一下梯度下降法

3.2 测试

首先我们假定一个函数f(x) $f(x) = 4x^{2} + 2x$ ,跟上面一样先求导，然后令导数 $8x + 2$ 为0，解得x=-0.25的时候该函数有最小值-0.25.

接下来我们用代码来实现：

def h(x):
    return 8*x+2

def Gradient_descent_test():
    x_old = -1
    x_new = 0
    a = 0.01
    presision = 0.0000001
    while abs(x_new - x_old) > presision:
        x_old = x_new
        x_new = x_old - a*h(x_old)
        print(x_new)
    print("结果：")
    print(x_new)

Gradient_descent_test()

基本与上面一样唯一不同的是+变成了-。

4. 随机梯度上升法

4.1 思想

不管是梯度上升法还是梯度下降法在每次更新回归系数的时候都需要遍历整个数据集，那么当我们数据集很多的时候，不管是效率还是计算的复杂度就会很高，那么我们需要去改进方法，我们可以一次仅仅只使用一个样本点来更新回归系数，改进后的方法称为随机梯度上升算法。

该算法的伪代码为

所有的回归系数初始化为1

对数据集中每个样本

计算该样本的梯度

使用alpha * gradient更新回归系数值

返回回归系数值

4.2 案例

def stocGradAscent0(dataMatrix,classLabels):
    m,n = np.shape(dataMatrix)
    alpha = 0.01#学习率
    weights = np.ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights



dataArr,labelMat = loadDataSet()
weights = stocGradAscent0(np.array(dataArr),labelMat)
plotBestFit(weights)

我们可以看到结果并没有梯度上升算法的结果好，但是这样比是不公平的，因为我们可以看到梯度上升法的结果是在数据集迭代了500次得出的，所以我们还要对算法进行改进。

4.3 改进的随机梯度上升法

import random


def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

主要改进的地方有两处，第一处是alpha每次迭代的时候都会调整，并且它随着迭代次数的不断减小也不会减小到0，因为有一个常数项0.01，这样做是为了保证在多次迭代后新数据对结果也具有一定的影响力。

第二处是采用随机选取样本来更新回归系数，这样可以减少周期性的波动。

我们可以看到改进后的结果相比没改进前改善了很多。

五、实战

1.准备数据

对数据集进行预处理，我们需要做两件事，第一，所有缺失值必须用一个实数值来代替，第二，如果在测试数据集中发现了一条数据的类别标签已经缺失的话，我们最简单的做法是将该条数据丢弃。

2. 测试算法

import numpy as np
import random

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        # dataIndex=range(m)
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.00001
            # randIndex = int(random.uniform(0,len(dataIndex)))
            randIndex = dataIndex[int(random.uniform(0, len(dataIndex)))]
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            # del(dataIndex[randIndex])
            dataIndex.remove(randIndex)
    return weights


def classifyVector(inX,weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5:
        return 1.0
    else:
        return 0.0
    

def colicTest():
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(len(currLine)-1):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[-1]))
    trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 600)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(len(currLine)-1):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), trainWeights))!= int(currLine[-1]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec) * 100
    print("the error rate of this test is: %f" % errorRate)
    return errorRate
    
def multiTest():
    numTests = 10
    errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print("after %d iterations the average error rate is: %f" % (numTests,errorSum/float(numTests)))


multiTest()