排序——堆排序

目录

1.什么是堆？

1.1大堆

1.2小堆

 2.如何调整成小堆或大堆（如何建堆）

2.1向下调整

3.堆排序

4.完整代码

---

1.什么是堆？

你可以把堆理解成一颗完全二叉树，它的结点并不一定是满的

那么堆又分为：1.大堆         2.小堆

1.1大堆

大堆就是这颗完全二叉树的父节点都大于他的子节点

例如这就是一个大堆

1.2小堆

小堆与大堆的区别就在于，小堆是每个父节点都小于他的子节点

 2.如何调整成小堆或大堆（如何建堆）

我们将堆看做是一颗完全二叉树这是一种抽象的看法

 

我们要排序的是一个数组，我们要将这个数组排成小堆或者大堆

2.1向下调整

我们的向下调整的思路是这样的：

用左右子节点中较小的那一个，去与根节点比较，如果要比根节点小的话，就交换

tips：左子节点=父节点*2+1，右子节点=父节点*2+2

        父节点=（子节点-1）/2

void AdjustHeap(int* arr,int n,int root)
{
	int partent = root;//将根节点作为父节点
	int child = partent * 2 + 1;//默认小的那个是父节点的左子节点
	while (child<n)//孩子节点不能大于n
	{
		if (child+1 < n&& arr[child + 1] < arr[child]）
		{
          //child+1 < n这里如果只有一个左子节点，此时child+1就等于n，再去+1访问右子节点就会越界

			child += 1;//如果右子节点要大，那么child就+走到右子节点
		}
		if (arr[child] < arr[partent])//将左右节点中较小的那个数与根节点比较，如果小的话
		{
			Swap(&arr[child], &arr[partent]);//交换根节点与较小的那个子节点
			partent = child;//将较小的那个结点重新当做父节点
			child = partent * 2 + 1;//重新赋为左子节点
		}
		else
			break;
	}
}

那么这只是排一个子树，那么我们要对整个树都进行向下调整，就需要循环

for (int i = (n - 2) / 2; i >= 0; --i)
//n为数组的总数，n-1为最后一个子节点，（n-1-1）/2就是父节点
	{
		AdjustHeap(arr,n,i);
	}

经历完这几部，我们的数组就可以抽象看成一个小堆

3.堆排序

经过上面的步骤，我相信你已经可以排序成一个小堆或者大堆

那么这里有一个问题：

我们想要将数组排成升序，应该是用大堆还是小堆？

答案是大堆。

思想如下：排大堆，将大堆的根与最后交换，然后将交换过的那个踢出堆，然后再排大堆，然后再交换........

 

 

 

 

 

 

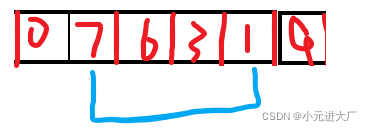
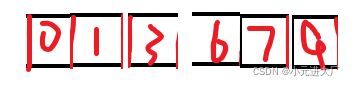
	int end = n - 1;
	while (end)
	{
		Swap(&arr[0], &arr[end]);
		AdjustHeap(arr, end, 0);
		--end;
	}

4.完整代码

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}
void AdjustHeap(int* arr,int n,int root)
{
	int partent = root;
	int child = partent * 2 + 1;
	while (child<n)
	{
		if (child+1 <n && arr[child + 1] > arr[child])
		{
			child += 1;
		}
		if (arr[child] > arr[partent])
		{
			Swap(&arr[child], &arr[partent]);
			partent = child;
			child = partent * 2 + 1;
		}
		else
			break;
	}
}

void HeapSort(int* arr,int n)
{
	for (int i = (n - 2) / 2; i >= 0; --i)
	{
		AdjustHeap(arr,n,i);
	}

	int end = n - 1;
	while (end)
	{
		Swap(&arr[0], &arr[end]);
		AdjustHeap(arr, end, 0);
		--end;
	}
}