四阶阿当姆斯显格式求解常微分方程

在前面的数值方法中，使用的都是单步法，就是在计算时只用到前一步的值，所以若要提高精度，就要增加中间函数值的计算，这就大大增加了计算量，然而事实上，前面所计算的都已经知道了，而前面计算越早得出的结果数值逼近效果更好，因此若这些前面计算所得值不用是非常可惜的，由此产生了阿当姆斯方法，它充分利用了前面所计算的值，并且使得精度大大提高，同样，本文仍不侧重理论分析，况且其精度分析并不难，只需利用泰勒展开即可，感兴趣的伙伴可以自行证明和分析，下面先给出四阶阿当姆斯显格式，至于更高阶或者低阶的阿当姆斯格式，读者可参考以下代码进行编写与练手。

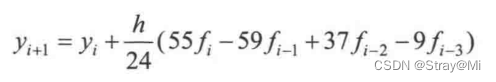
 数值算例与前面几篇文章相同。

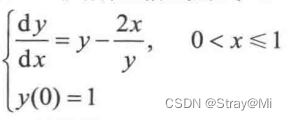
 MATLAB主函数如下：

% 四阶啊当姆斯显格式，由于其是多步法，因此除了需要知道y0以外还要知道y1,y2,y3，为了保持四阶精度，采用四阶龙格计算
function [err]=Adams_explicit(L,h)
x=(0:h:L);
n=length(x);
% 精确解
for i=1:n
    ye(i)=sqrt(1+2*x(i));
end
% 定义初始条件
yc(1)=1;
% 定义右端项函数
f=@(x,y) y-2*x/y;
% 利用四阶龙格计算y1,y2,y3
for i=1:3
    k1=h*f(x(i),yc(i));
    k2=h*f(x(i)+h/2,yc(i)+k1/2);
    k3=h*f(x(i)+h/2,yc(i)+k2/2);
    k4=h*f(x(i)+h,yc(i)+k3);
    yc(i+1)=yc(i)+1/6*(k1+2*k2+2*k3+k4);
end
% 由啊当姆斯计算数值解
for i=4:n-1
    yc(i+1)=yc(i)+h/24*(55*f(x(i),yc(i))-59*f(x(i)-h,yc(i-1))+37*f(x(i)-2*h,yc(i-2))-9*f(x(i)-3*h,yc(i-3)));
end
% 计算误差
err=abs(ye-yc);

 收敛阶计算代码如下：
 

% 计算四阶啊当姆斯显格式收敛阶
dh=[1/50,1/100,1/200,1/400,1/800];
n=length(dh);
for i=1:n
    e(i)=max(Adams_explicit(1,dh(i)));
end
for i=1:n-1
    rate_Adams_explicit(i)=log2(e(i)/e(i+1));
end
% 由结果可以知道，啊当姆斯显格式是四阶收敛的

 Python代码如下：

import numpy as np
# 计算数值解
def Adams_Bashforth(f,x,y0,h,args=()):
    """

    :param f: 右端项函数
    :param x: 求解区间离散化
    :param y0: 初值
    :param h: 步长
    :param args:
    :return: 返回数值解
    """
    n = len(x)
    # 初始化数值解
    y = np.empty((n, 1), dtype=float)
    # 初值
    y[0] = y0
    for i in range(3):
        k1 = h * f(x[i], y[i], *args)
        k2 = h * f(x[i] + 1 / 2 * h, y[i] + 1 / 2 * k1, *args)
        k3 = h * f(x[i] + 1 / 2 * h, y[i] + 1 / 2 * k2, *args)
        k4 = h * f(x[i] + h, y[i] + k3, *args)
        y[i + 1] = y[i] + (k1 + 2 * k2 + 2 * k3 + k4) / 6
    for i in range(3,n-1):
        y[i+1]=y[i]+h/24*(55*f(x[i],y[i])-59*f(x[i]-h,y[i-1])+37*f(x[i]-2*h,y[i-2])-9*f(x[i]-3*h,y[i-3]))
    return y


# 计算精确解
def y_exact(x):
    n = len(x)
    ye = np.empty((n, 1), dtype=float)
    for i in range(n):
        ye[i] = np.sqrt(1 + 2 * x[i])
    return ye


# 计算误差
def err(h):
    x = np.linspace(0, 1, num=int(1 / h + 1))
    y = Adams_Bashforth(lambda x, y: y - 2 * x / y, x, 1, h)
    ye = y_exact(x)
    # 计算误差
    # err=np.empty((len(x), 1), dtype=float)
    err = np.abs(y - ye)
    return err


# 计算收敛阶
dh = [1/50,1 / 100, 1 / 200, 1 / 400, 1 / 800]
m = len(dh)
e = []
for i in range(m):
    error = max(err(dh[i]))
    e.append(error)
for i in range(m - 1):
    rate = np.log2(e[i] / e[i + 1])
    print(rate)
# 所得结果与MATLAB计算所得是一致的

总结：虽然四阶阿当姆斯显格式充分利用了前面所计算的值，从而大大提高了精度，但是其仍需要的值，因此需要选择合适的方法计算这些值，否则则会导致数值实验结果与理论精度不一致，并且通过实验也可以发现，要想达到四阶精度，其步长需要尽可能的小，否则也会与理论不符，最后，今天的更新就到此为止啦，伙伴们也可以自行优化代码从而使得与MATLAB的代码量接近，创作不易，还望伙伴们多多支持~