为什么大部分小数在计算机中是不精确的

文章目录

• • 概要
  • 整体架构流程
  • 技术名词解释
  • 技术细节
  • 小结

概要

浮点型数字（俗称小数）大部分在计算机中是不精确的，的原因是，计算机是以二进制进行运算的 ，转化为二进制制的时候，小数部分存在可能是无限循环，因此取近似值，（数值不是十进制里面准确的），所以就出现了精度丢失。类似于我们平常所知十进制，1/3，我们在正常的数学运算中就无法去表示它，只能写成分数。

整体架构流程

   数字在计算机中是采用二进制存储的，在将小数存入计算机中时，要将十进制转为二进制，最后呈现给我们的是二进制在重新转换为十进制的结果。而在十进制转换为二进制的过程中，极易出现无限循环的情况，因此小数将变得不再精确。计算机最终会取一个无限接近结果的小数作为结果。

        十进制数转换为二进制数时，需要对整数部分与小数部分分别进行转换。

（1）整数部分转换步骤
        1.使用十进制的值除以2，得到两个部分，商和余数；

        2.商继续除以2，直到商为0为止；

        3.余数倒着看，就是二进制的值。

（2） 小数部分转换步骤
        1.整数部分转整数部分，小数部分转小数部分；

        2.把十进制的小数乘以2：

                (1).结果如果大于1，转换后的小数后面记1；

                (2).结果如果小于1，转换后的小数后面记0。

        3.直到结果为1.0为止。

十进制小数转化为二进制小数大部分是不精确的，计算示例

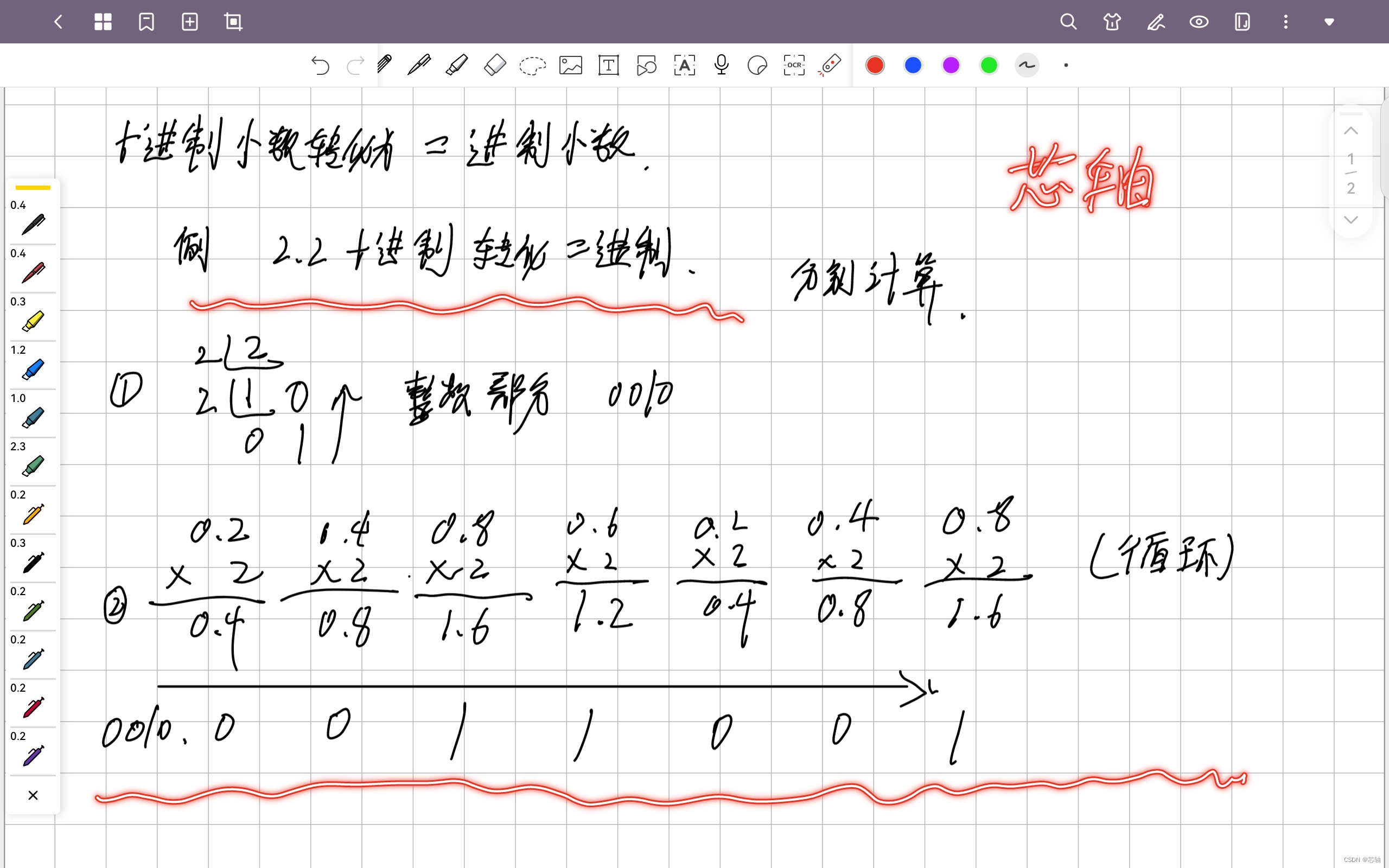
在十进制转换为二进制的过程中，极易出现无限循环的情况，因此小数将变得不再精确。计算机最终会取一个无限接近结果的小数作为结果。因此就出现了精度丢失的情况

精度运算丢失的解决办法

现有有三种办法

1. 如果业务不是必须非常精确的要求可以采取四舍五入的方法来忽略这个问题。
2. 转成整型再进行计算。
3. 使用 BCD 码存储和运算二进制小数(感兴趣的可自行搜索学习)。

一般每种语言都用高精度运算的解决方法（比一般运算耗费性能），Java 的 BigDecimal，但是一定要把小数转成字符串传入构造，不然还是有坑，其他语言大家可以自行寻找一下

技术名词解释

直到1985年，IEEE 组织推出了浮点数标准，就是我们经常听到的 IEEE754 浮点数标准，这个标准统一了浮点数的表示形式，并提供了 2 种浮点格式：

• 单精度浮点数 float：32 位，符号位 S 占 1 bit，指数 E 占 8 bit，尾数 M 占 23 bit
• 双精度浮点数 float：64 位，符号位 S 占 1 bit，指数 E 占 11 bit，尾数 M 占 52 bit

为了使其表示的数字范围、精度最大化，浮点数标准还对指数和尾数进行了规定：

1. 尾数 M 的第一位总是 1（因为 1 <= M < 2），因此这个 1 可以省略不写，它是个隐藏位，这样单精度 23 位尾数可以表示了 24 位有效数字，双精度 52 位尾数可以表示 53 位有效数字
2. 指数 E 是个无符号整数，表示 float 时，一共占 8 bit，所以它的取值范围为 0 ~ 255。但因为指数可以是负的，所以规定在存入 E 时在它原本的值加上一个中间数 127，这样 E 的取值范围为 -127 ~ 128。表示 double 时，一共占 11 bit，存入 E 时加上中间数 1023，这样取值范围为 -1023 ~ 1024。

除了规定尾数和指数位，还做了以下规定：

• 指数 E 非全 0 且非全 1：规格化数字，按上面的规则正常计算
• 指数 E 全 0，尾数非 0：非规格化数，尾数隐藏位不再是 1，而是 0(M = 0.xxxxx)，这样可以表示 0 和很小的数
• 指数 E 全 1，尾数全 0：正无穷大/负无穷大（正负取决于 S 符号位）
• 指数 E 全 1，尾数非 0：NaN(Not a Number)

技术细节

浮点数为什么有精度损失？

我们再来看一下，平时经常听到的浮点数会有精度损失的情况是怎么回事？

如果我们现在想用浮点数表示 0.2，它的结果会是多少呢？

0.2 转换为二进制数的过程为，不断乘以 2，直到不存在小数为止，在这个计算过程中，得到的整数部分从上到下排列就是二进制的结果。

0.2 * 2 = 0.4 -> 0
0.4 * 2 = 0.8 -> 0
0.8 * 2 = 1.6 -> 1
0.6 * 2 = 1.2 -> 1
0.2 * 2 = 0.4 -> 0（发生循环）
...

所以 0.2(D) = 0.00110...(B)。

因为十进制的 0.2 无法精确转换成二进制小数，而计算机在表示一个数字时，宽度是有限的，无限循环的小数存储在计算机时，只能被截断，所以就会导致小数精度发生损失的情况。

小结

计算机使用二进制运算，程序中的十进制数字先转换成二进制，再进行运算。Float和Double的小数部分在转换为二进制的过成中容易产生无限循环的情况，通常都是取无限接近于原值的近似值，所以导致出现精度丢失的情况。

1. 浮点数一般用科学计数法表示
2. 把科学计数法中的变量，填充到固定 bit 中，即是浮点数的结果
3. 在浮点数提出的早期，各个计算机厂商各自制定自己的浮点数规则，导致不同厂商对于同一个数字的浮点数表示各不相同，在计算时还需要先进行转换才能进行计算
4. 后来 IEEE 组织提出了浮点数的标准，统一了浮点数的格式，并规定了单精度浮点数 float 和双精度浮点数 double，从此以后各个计算机厂商统一了浮点数的格式，一直延续至今
5. 浮点数在表示小数时，由于十进制小数在转换为二进制时，存在无法精确转换的情况，而在固定 bit 的计算机中存储时会被截断，所以浮点数表示小数可能存在精度损失
6. 浮点数在表示一个数字时，其范围和精度非常大，所以我们平时使用的小数，在计算机中通常用浮点数来存储