笔试强训题（5）

于 2025-03-24 15:04:02 发布
阅读量1k 收藏 21
点赞数 15
分类专栏： 算法题 文章标签： 算法 面试 c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_65558082/article/details/146369170
版权

目录

1. Day25

1.1 笨小猴（模拟）

  1. 题目链接： BC145 [NOIP2008]笨小猴
  2. 题目描述：

  1. 解法：
    • 算法思路：根据题意模拟，但是要注意细节。
  2. C++ 算法代码：
#include <iostream>
#include <cmath>
using namespace std;

bool check(int n)   // 判断 n 是否是质数
{
    if(n < 2)
    {
        return false;
    }

    for(int i = 2; i <= sqrt(n); i++)
    {
        if(n % i == 0)
        {
            return false;
        }
    }

    return true;
}

int main()
{
    string s;
    cin >> s;

    int hash[26] = {0};
    int maxn = -1;
    int minn = 100;
    for(auto& ch : s)
    {
        hash[ch - 'a']++;
    }

    for(int i = 0; i < 26; i++)
    {
        if(hash[i])
        {
            maxn = max(maxn, hash[i]);
            minn = min(minn, hash[i]);
        }
    }

    if(check(maxn - minn))
    {
        cout << "Lucky Word" << endl;
        cout << maxn - minn << endl;
    }
    else 
    {
        cout << "No Answer" << endl;
        cout << 0 << endl;
    }

    return 0;
}

1.2 主持人调度（⼀）（排序）

  1. 题目链接： NC383 主持人调度（⼀）
  2. 题目描述：

  1. 解法：
    • 算法思路：
      • 区间问题技巧：左端点排序或者按照右端点排序。
      • 左端点排序后，我们仅需考虑后续区间是否能与前⼀个区间重叠即可，美滋滋。
  2. C++ 算法代码：
class Solution {
  public:

    bool hostschedule(vector<vector<int> >& schedule) 
    {
        sort(schedule.begin(), schedule.end());
        for (int i = 1; i < schedule.size(); i++) 
        {
            if (schedule[i][0] < schedule[i - 1][1])
            {
                return false;
            }
        }

        return true;
    }
};

1.3 分割等和子集（动态规划 - 01背包）

  1. 题目链接： DP45 分割等和子集
  2. 题目描述：

  1. 解法：
    • 算法思路：01 背包问题：原问题转换成，从 n 个数中选，总和恰好为 sum / 2，能否挑选出来。
  2. C++ 算法代码：
#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n = 0;
    cin >> n;
    vector<int> nums(510);
    int sum = 0;
    for(int i = 0; i < n; i++)
    {
        cin >> nums[i];
        sum += nums[i];
    }

    if(sum % 2 == 1)
    {
        cout << "false" << endl;
    }
    else 
    {
        sum /= 2;
        vector<bool> dp(sum + 1);
        dp[0] = true;
        for(int i = 0; i < n; i++)
        {
            for(int j = sum; j >= nums[i]; j--)
            {
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }

        if(dp[sum])
        {
            cout << "true" << endl;
        }
        else 
        {
            cout << "false" << endl;
        }
    }

    return 0;
}

2. Day26

2.1 小红的ABC（字符串 + 找规律）

  1. 题目链接： 小红的ABC
  2. 题目描述：

  1. 解法：
    • 算法思路：
      • 由于题目要找的是最短的回文子串，并且只有三个字母 a b c，因此最短的回文子串的长度要么是 2，要么是 3。 因此，我们仅需枚举所有的二元组以及三元组就好了。
  2. C++ 算法代码：
#include <iostream>
using namespace std;

int main()
{
    string s;
    cin >> s;
    
    int ret = -1;
    int n = s.size();
    for(int i = 0; i < n; i++)
    {
        if(i + 1 < n && s[i] == s[i + 1])
        {
            ret = 2;
            break;
        }
        
        if(i + 2 < n && s[i] == s[i + 2])
        {
            ret = 3;
        }
    }
    
    cout << ret << endl;
    
    return 0;
}

2.2 不相邻取数（动态规划 - 线性 dp）

  1. 题目链接： DP23 不相邻取数
  2. 题目描述：

  1. 解法：
    • 算法思路：打家劫舍~
  2. C++ 算法代码：
#include <iostream>
using namespace std;

const int N = 2e5 + 10;

int main()
{
    int n = 0;
    cin >> n;

    int arr[N] = {0};
    for(int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }

    int f[N] = {0};     // 选择当前数字
    int g[N] = {0};     // 不选当前数字
    for(int i = 1; i <= n; i++)
    {
        // f[i] = max(f[i - 1], g[i - 1] + arr[i]);
        f[i] = g[i - 1] + arr[i];
        g[i] = max(f[i - 1], g[i - 1]);
    }

    cout << max(f[n], g[n]) << endl;

    return 0;
}

2.3 空调遥控（二分 / 滑动窗口）

  1. 题目链接： 空调遥控
  2. 题目描述：

  1. 解法：
    • 算法思路：先排序。
      • 解法一：滑动窗口。维护窗口内最大值与最小值的差在 2 * p 之间。
      • 解法二：二分查找。枚举所有的温度，二分出符合要求的学生区间，然后统计个数。
  2. C++ 算法代码：
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1e6 + 10;

int main()
{
    int n, p;
    cin >> n >> p;
    
    int arr[N];
    for(int i = 0; i < n; i++)
    {
        cin >> arr[i];
    }
    
    sort(arr, arr + n);
    int ret = 0;
    int left = 0;
    int right = 0;
    p *= 2;
    while(right < n)
    {
        while(arr[right] - arr[left] > p)
        {
            left++;
        }
        
        ret = max(ret, right - left + 1);
        right++;
    }
    
    cout << ret << endl;
    
    return 0;
}

3. Day27

3.1 kotori和气球（组合数学）

  1. 题目链接： kotori和气球
  2. 题目描述：

  1. 解法：
    • 算法思路：简单的排列组合问题，结果等于 n 与 m 个 n - 1 的乘积。
  2. C++ 算法代码：
#include <iostream>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    
    int ret = n;
    for(int i = 1; i < m; i++)
    {
        ret = (ret * (n - 1)) % 109;
    }
    
    cout << ret << endl;
    
    return 0;
}

3.2 走迷宫（BFS）

  1. 题目链接： AB20 走迷宫
  2. 题目描述：

  1. 解法：
    • 算法思路：简单 bfs 应用题。
  2. C++ 算法代码：
#include <iostream>
#include <cstring>
#include <queue>
#include <utility>
using namespace std;

const int N = 1010;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};

int n, m;
int x1, y1, x2, y2;

char arr[N][N];
int dist[N][N]; // [i, j] 位置是否已经搜索过，以及到达 [i, j] 位置的最短距离

int bfs()
{
    if(arr[x2][y2] == '*')
    {
        return -1;
    }

    memset(dist, -1, sizeof(dist)); // 表⽰还没开始搜索
    queue<pair<int, int>> q;
    q.push(make_pair(x1, y1));
    dist[x1][y1] = 0;
    while(q.size())
    {
        auto [a, b] = q.front();
        q.pop();
        for(int k = 0; k < 4; k++)
        {
            int x = a + dx[k];
            int y = b + dy[k];
            if(x >= 1 && x <= n && y >= 0 && y <= m && arr[x][y] == '.' && dist[x][y] == -1)
            {
                q.push(make_pair(x, y));
                dist[x][y] = dist[a][b] + 1;
                if(x == x2 && y == y2)
                {
                    return dist[x][y];
                }
            }
        }
    }

    return -1;
}

int main() 
{
    cin >> n >> m;
    cin >> x1 >> y1 >> x2 >> y2;

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> arr[i][j];
        }
    }

    cout << bfs() << endl;

    return 0;
}

3.3 主持人调度（二）（贪心 + 优先级队列）

  1. 题目链接： NC147 主持人调度（二）
  2. 题目描述：

  1. 解法：
    • 算法思路。左端点排序，然后搞个堆：
      • 先把第一个区间的右端点加入到堆中；
      • 遍历后面的区间，分情况讨论：
        • 如果左端点大于等于堆顶元素，能接在后面，干掉堆顶，然后把这个区间的右端点加入堆；
        • 否则的话，只能再来⼀个人，只把这个区间的右端点加入堆。
      • 最后堆的大小就是需要的人数。
  2. C++ 算法代码：
#include <queue>
class Solution {
public:

    int minmumNumberOfHost(int n, vector<vector<int> >& startEnd) 
    {
        sort(startEnd.begin(), startEnd.end());

        priority_queue<int, vector<int>, greater<int>> heap;    // 创建⼀个⼩根堆
        heap.push(startEnd[0][1]);
        for(int i = 1; i < startEnd.size(); i++)
        {
            if(startEnd[i][0] < heap.top())
            {
                heap.push(startEnd[i][1]);
            }
            else 
            {
                heap.pop();
                heap.push(startEnd[i][1]);
            }
        }

        return heap.size();
    }
};

4. Day28

4.1 游游的重组偶数（数学）

  1. 题目链接： [编程题]游游的重组偶数
  2. 题目描述：

  1. 解法：
    • 算法思路：
      • 偶数的性质就是最后⼀位能被 2 整除即可。
      • 因此，把该数中能被 2 整除的数字放在最后就好了，但是注意不要出现前导零。
  2. C++ 算法代码：
#include <iostream>
using namespace std;

int main() 
{
    int q = 0;
    cin >> q;
    string s;
    while(q--)
    {
        cin >> s;

        int n = s.size();
        // if((s[n - 1] - '0') % 2 == 0)
        // {
        //     cout << s << endl;
        //     continue;
        // }

        // if(n == 1)
        // {
        //     cout << -1 << endl;
        // }

        // for(int i = n - 2; i >= 0; i--)
        // {
        //     if((s[i] - '0') % 2 == 0)
        //     {
        //         swap(s[i], s[n - 1]);
        //         cout << s << endl;
        //         break;
        //     }

        //     if(i == 0)
        //     {
        //         cout << -1 << endl;
        //     }
        // }

        for(int i = n - 1; i >= 0; i--)
        {
            if((s[i] - '0') % 2 == 0)
            {
                swap(s[i], s[n - 1]);
                break;
            }
        }

        if((s[n - 1] - '0') % 2 == 0)
        {
            cout << s << endl;
        }
        else
        {
            cout << -1 << endl;
        }
    }

    return 0;
}

4.2 体操队形（DFS + 枚举）

  1. 题目链接： 体操队形
  2. 题目描述：

  1. 解法：
    • 算法思路：画出决策树，注意剪枝策略~
  2. C++ 算法代码
#include <iostream>
using namespace std;

const int N = 15;

bool vis[N];
int arr[N];
int ret = 0;
int n = 0;

void dfs(int pos)
{
    if(pos == n + 1)
    {
        ret++;
        return;
    }
    
    for(int i = 1; i <= n; i++)
    {    
        if(vis[i])    // 当前 i 已经放过了 - 剪枝
        {
            continue;
        }
        
        if(vis[arr[i]])    // 剪枝
        {
            return;
        }
        
        vis[i] = true;    // 相当于放上 i 号队员
        dfs(pos + 1);
        vis[i] = false;   // 回溯- 还原现场
    }
}

int main()
{
    cin >> n;
        
    for(int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }
    
    dfs(1);
    
    cout << ret << endl;
    
    return 0;
}

4.3 二叉树中的最大路径和（树形dp）

  1. 题目链接： NC6 二叉树中的最大路径和
  2. 题目描述：

  1. 解法：
    • 算法思路。树形dp：
      • 左子树收集：以左子树为起点的最大单链和；
      • 右子树收集：以右子树为起点的最大单链和；
      • 根节点要做的事情：整合左右子树的信息，得到经过根节点的最大路径和；
      • 向上返回：以根节点为起点的最大单链和；
  2. C++ 算法代码：
/**
 * struct TreeNode {
 *	int val;
 *	struct TreeNode *left;
 *	struct TreeNode *right;
 *	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
public:
    int ret = -1010;

    int maxPathSum(TreeNode* root) 
    {
        dfs(root);
        return ret;
    }

    int dfs(TreeNode* root)
    {
        if(root == nullptr)
        {
            return 0;
        }

        int left = max(dfs(root->left), 0);
        int right = max(dfs(root->right), 0);

        ret = max(ret, root->val + left + right);
        return max(left, right) + root->val;
    }
};

5. Day29

5.1 排序子序列（模拟）

  1. 题目链接： [编程题]排序子序列
  2. 题目描述：

  1. 解法：
    • 算法思路：根据题意，用指针模拟即可。（注意：本道题的测试数据不严谨，有可能错误的代码也能提交过~）
  2. C++ 算法代码：
#include <iostream>
using namespace std;

const int N = 1e5 + 10;

int main() 
{
    int n = 0;
    cin >> n;
    int arr[N] = {0};
    for(int i = 0; i < n; i++)
    {
        cin >> arr[i];
    }

    int ret = 0;
    int i = 0;
    while(i < n)
    {
        if(i == n - 1)
        {
            ret++;
            break;
        }

        if(arr[i + 1] < arr[i])
        {
            while(i + 1 < n && arr[i] >= arr[i + 1])
            {
                i++;
            }

            ret++;
        }
        else if(arr[i + 1] > arr[i])
        {
            while(i + 1 < n && arr[i] <= arr[i + 1])
            {
                i++;
            }

            ret++;
        }
        else
        {
            while(i + 1 < n && arr[i] == arr[i + 1])
            {
                i++;
            }
        }

        i++;
    }

    cout << ret << endl;

    return 0;
}

5.2 削减整数（贪心）

  1. 题目链接： 消减整数
  2. 题目描述：

  1. 解法：
    • 算法思路：贪心 + 数学。
      • 尽可能的翻倍；
      • 不能无脑翻倍，只能是 2 * cur 的倍数时，才能翻倍。
  2. C++ 算法代码：
#include <iostream>
using namespace std;

int t, h;

int fun()
{
    int ret = 0;
    int a = 1;
    while(h)
    {
        ret++;
        h -= a;
        if(h % (a * 2) == 0)
        {
            a *= 2;
        }
    }
    
    return ret;
}

int main()
{
    cin >> t;
    while(t--)
    {
        cin >> h;
        cout << fun() << endl;
    }
    
    return 0;
}

5.3 最长上升子序列(二)（贪心 + 二分）

  1. 题目链接： NC164 最长上升子序列(二)
  2. 题目描述：

  1. 解法：
    • 算法思路：
      • 我们在考虑最长递增子序列的长度的时候，其实并不关心这个序列长什么样子，我们只是关心最后⼀个元素是谁。这样新来⼀个元素之后，我们就可以判断是否可以拼接到它的后⾯。
      • 因此，我们可以创建⼀个数组，统计长度为 x 的递增子序列中，最后一个元素是谁。为了尽可能的让这个序列更长，我们仅需统计长度为 x 的所有递增序列中最后⼀个元素的「最小值」。
      • 统计的过程中发现，数组中的数呈现「递增」趋势，因此可以使用「二分」来查找插入位置。
  2. C++ 算法代码：
class Solution {
    int dp[100010] = { 0 }; // dp[i] 表⽰：⻓度为 i 的最⼩末尾
    int pos = 0;

  public:

    int LIS(vector<int>& a) 
    {
        for (auto x : a) 
        {
            // 查找 x 应该放在哪个位置
            if (pos == 0 || x > dp[pos]) 
            {
                dp[++pos] = x;
            } 
            else 
            {
                // ⼆分查找插⼊位置
                int l = 1, r = pos;
                while (l < r) 
                {
                    int mid = (l + r) / 2;
                    if (dp[mid] >= x) r = mid;
                    else l = mid + 1;
                }

                dp[l] = x;
            }
        }
        
        return pos;
    }
};

6. Day30

6.1 爱吃素（数学）

  1. 题目链接： 爱吃素
  2. 题目描述：

  1. 解法：
    • 算法思路：判断两数相乘是否是素数。
      • 不能直接乘起来然后判断，因为数据量太大了，不仅存不下，而且会超时；
      • 因此根据素数的性质，分类讨论。
      • bool isPrime(int number); 函数的功能是判断素数。返回一个和A一样大小的数组， 如果A中某个数是素数， 在tf中对应位置为逻辑1， 否则为0。其中A中元素要求是正整数。
  2. C++ 算法代码：
#include <iostream>
#include <cmath>
using namespace std;

bool isprim(long long x)
{
    if(x < 2)
    {
        return false;
    }
    
    for(int i = 2; i <= sqrt(x); i++)
    {
        if(x % i == 0)
        {
            return false;
        }
    }
    
    return true;
}

int main()
{
    int t = 0;
    cin >> t;
    while(t--)
    {
        long long a, b;
        cin >> a >> b;
        if((a == 1 && isprim(b)) || (b == 1 && isprim(a)))
        {
            cout << "YES" << endl;
        }
        else
        {
            cout << "NO" << endl;
        }
    }
    
    return 0;
}

6.2 相差不超过k的最多数（滑动窗口）

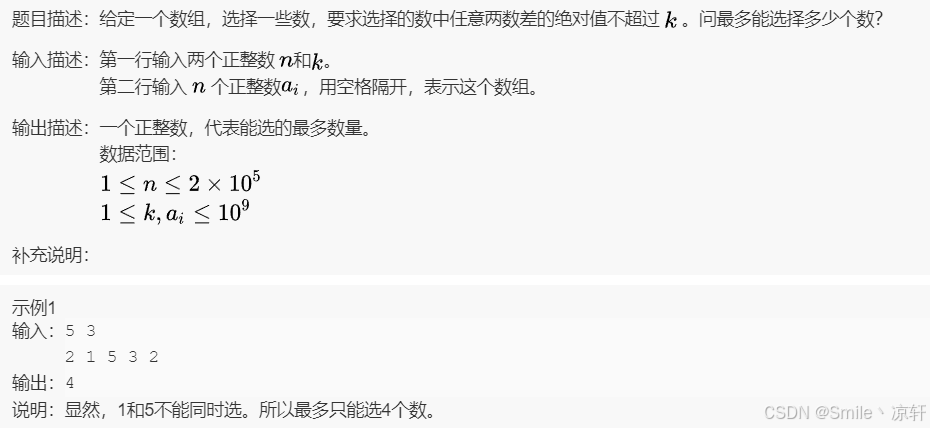
  1. 题目链接： AB33 相差不超过k的最多数
  2. 题目描述：

  1. 解法：
    • 算法思路：排序 + 滑动窗口
  2. C++ 算法代码：
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 2e5 + 10;

int main() 
{
    int n, k;
    cin >> n >> k;
    int arr[N];
    for(int i = 0; i < n; i++)
    {
        cin >> arr[i];
    }

    sort(arr, arr + n);
    int left = 0;
    int right = 0;
    int ret = 1;
    while(right < n)
    {
        if(arr[right] - arr[left] > k)
        {
            left++;
        }

        ret = max(ret, right - left + 1);
        right++;
    }

    cout << ret << endl;

    return 0;
}

6.3 最长公共子序列(一)（动态规划 - LCS）

  1. 题目链接： DP19 最长公共子序列(一)
  2. 题目描述：

  1. 解法：
    • 算法思路：经典两个字符串之间的 dp 问题。
      1. 状态表示： dp[i][j] 表示：字符串 s1 中 [0, i] 区间与字符串 s2 中 [0, j] 区间内所有的子序列中，最长公共子序列的长度是多少。
      2. 状态转移方程：根据最后一个位置的字符情况，划分问题：
        • s1[i] == s2[j]：dp[i][j] = dp[i - 1][j - 1] + 1；
        • s1[i] != s2[j]：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。
    • 为了防止越界，我们把字符串的起始位置从 1 开始计算。
  2. C++ 算法代码：
#include <iostream>
using namespace std;

const int N = 1010;

int main() 
{
    int n, m;
    cin >> n >> m;
    char s1[N];
    char s2[N];

    for(int i = 1; i <= n; i++)
    {
        cin >> s1[i];
    }

    for(int i = 1; i <= m; i++)
    {
        cin >> s2[i];
    }

    int dp[N][N] = {0};
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(s1[i] == s2[j])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            }
            else
            {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }

    cout << dp[n][m] << endl;

    return 0;
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Smile丶凉轩

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值