线性代数2

原创已于 2023-12-16 22:39:15 修改 · 735 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#线性回归 #算法 #回归

于 2023-12-14 23:29:15 首次发布

本文详细介绍了矩阵的基本概念，包括矩阵的定义、行列数、不同类型的矩阵（如实矩阵、复矩阵等）、转置、特殊矩阵（数量矩阵、对角线矩阵、对称矩阵和反对称矩阵）、逆矩阵、行列式以及秩的计算。此外，还涵盖了分块矩阵的运算和初等变换等内容。

矩阵

一.矩阵概念

$\begin{pmatrix} a11 &a12 &... &a1n \\ a21 &a22 &... &a2n \\ ...& ... &... &... \\ an1&an2 &... &ann \end{pmatrix}$ 数表 m*n的矩阵 m是行数 n是列数

1.1矩阵与行列数的差别

行列式矩阵

本质一个数数表

符号 $\begin{vmatrix} \end{vmatrix}$ () or [ ]

形状行数= 列数行数 != or = 列数

1.2各种矩阵：

只有实数的矩阵叫实矩阵，只有复数的矩阵叫复矩阵，只有一行矩阵的矩阵叫行矩阵，只有一列的矩阵叫列矩阵，只有0的矩阵叫0矩阵

单位阵：

$\begin{bmatrix} 1 & & & \\ & 1& & \\ & & 1& \end{bmatrix}$ 单位阵：主对角线都为1 ，其他都为0.省略了没写0

同型矩阵

1.3矩阵乘法

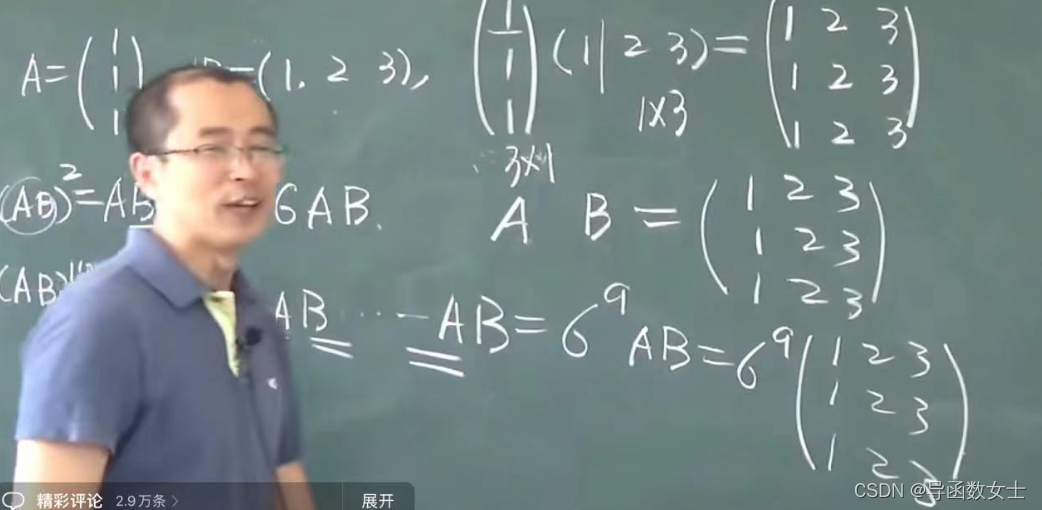
1.4矩阵幂运算

$A^{K}$ = A*A*A*....*A （共k个A）

$A^{0}$ = E

$A^{K1}A^{K2} = A^{K1+K2}$

$(A^{K1})^{K2} = A^{K1*K2}$

一般的

$AB^{K}! =A^{K}B^{K}$

$(AB)^{K}! = A^{2}B^{2}$

ABAB! = AABB

二.转置（ $A^{T}$ ）

A = $\begin{pmatrix} 1 &2 &3 \\ 1&1 &1 \end{pmatrix}$ $A^{T}$ = $\begin{pmatrix} 1 &1 \\ 2&1 \\ 3& 1 \end{pmatrix}$ $(A^{T})^{T}$ = $\begin{pmatrix} 1 &2 &3 \\ 1&1 &1 \end{pmatrix}$

2.1转置的性质

$(A^{T})^{T}$ = $A^{}$

$(A+B)^{T} = A^{T} +B^{T}$

$(kA)^{T} = kA^{T}$

*** $(AB)^{T} = B^{T}A^{T}$

三.特殊矩阵

3.1 数量矩阵：主对角线数全部相等，其余的为0

$\begin{pmatrix} a & & & \\ & a & & \\ & &a & \end{pmatrix}$ = aE aE = Ea = a

数量矩阵相加相减还是数量矩阵

$\begin{pmatrix} 1 & & & \\ &1 & & \\ & &1 & \end{pmatrix}$ + $\begin{pmatrix} 2 & & & \\ &2 & & \\ & &2 & \end{pmatrix}$ = $\begin{pmatrix} 3 & & & \\ &3 & & \\ & &3 & \end{pmatrix}$

3.2对角线矩阵（都为方阵）

$\begin{pmatrix} a1& & & \\ &a2 & & \\ & &a3 & \end{pmatrix}$ 主对角线可以不相等，其余的为0 可以用diag（a1,a2,a3...an）

对角线乘法：

$\begin{pmatrix} k1 & & \\ & k2 & \\ & &k3 \end{pmatrix}$ * $\begin{pmatrix} 1 &2 &3 \\ 2& 2& 2\\ 8&8 &8 \end{pmatrix}$ = ${\begin{pmatrix} k1&2k1 &3k1 \\ 2k2 &2k2 &2k2 \\ 8k3&8k3 &8k3 \end{pmatrix}}{}$ 左乘->行

$\begin{pmatrix} 1 &2 &3 \\ 2& 2& 2\\ 8&8 &8 \end{pmatrix}$ * $\begin{pmatrix} k1 & & \\ & k2 & \\ & &k3 \end{pmatrix}$ = $\begin{pmatrix} 1k1 & 2k2 & 3k3\\ 2k1& 2k2& 2k3\\ 8k1& 8k2& 8k3 \end{pmatrix}$ 右乘->列

3.3对称矩阵(与行列式的对称差不多)

$\begin{pmatrix} 1 &2&3 \\ 2&1 &4 \\ 3& 4 & 1 \end{pmatrix}$ 主对角线没有要求，其余的上下数一样

$a_{ij} = a_{ji}$

$A^{T} = A_{}$

$(A+B)^{T} = A^{T} +B^{T}$ = $A^{} +B^{}$

$(kA)^{T} = kA^{T}$ = $kA^{}$

$(AB)^{T} = B^{T}A^{T}$ $=B^{}A^{}! = A^{}B^{}$

3.4反对称矩阵

$\begin{pmatrix} 0 &1 &-3 \\ -1&0 &-4 \\ 3& 4 & 0 \end{pmatrix}$ 主对角线全为0，其余的上下成相反数 对称矩阵主对角线没有要求

$a_{ij} = -a_{ji}$

$a_{ij} = 0$

$A^{T} =- A_{}$

四.逆矩阵

逆矩阵：矩阵的除法 $A^{'}A^{}= 1$ 永远不要把放矩阵放在分母上

4.1方阵的行列式

$A^{} = \begin{pmatrix} 1&1 &1 \\ 2& 2 &2 \\ 3&3 &3 \end{pmatrix}$ $\left | A \right | = \begin{vmatrix} 1 &1&1 \\ 2& 2 & 2\\ 3&3 &3 \end{vmatrix}$

方阵行列式的性质

$\left | A^{T} \right | = \left | A^{} \right |$

$\left | kA \right | = k^{n}\left | A^{} \right |$ $_{n}$ 是行列式的行数

$\left | A^{}B^{} \right |$ $=\left | A \right |*\left |B \right |$

4.2伴随矩阵：只有方阵才有伴随矩阵

$A^{} = \begin{pmatrix} 1 &1 &1 \\ 2&1 &3 \\ 1& 1 &4 \end{pmatrix}$ 原矩阵

$A_{11} =1 A_{12} =-5 A_{13} =1,$

$A_{21} =-3 A_{22} =3 A_{23} =0$ ,

$A_{31} =2 A_{32} =-1 A_{33} =-1$ 代数余子式

$A^{*} =$ $\begin{pmatrix} 1 &-3 &2 \\ -5& 3& -1\\ 1&0 &-1 \end{pmatrix}$ 伴随矩阵

1 求出所有元素的代数余子式

2 按行求的代数余子式按列放构成伴随矩阵记作 $A^{*}$

4.2.1 伴随矩阵定理

定理

一 $A^{}A^{*} = A^{*}A^{} = \left | A \right |E$

二 $\left | A^{*} \right | =| A|^{n-1}$

三 $A^{-1} = \frac{1}{\left | A \right |}*A^{*}$

四若 $A$ 可逆， $\left | A^{-1} \right | = \left | A \right |^{-1}$ (A行列式值分之一 10 ，1/10)

证明四： $AA^{-1} = E, \left | A \right |\left | A^{-1} \right | = 1 ,\left | A^{-1} \right | = \frac{1}{\left | A \right |} = \left | A \right |^{-1}$

五若A可逆， $A^{*}$ 也可逆，则 $(A^{*})^{-1} = \frac{1}{\left | A \right |}A$

证明五：因为 $A^{}A^{*} = A^{*}A^{} = \left | A \right |E$ 等式左右同时除以 $\left | A \right |$ ,

则 $(\frac{1}{\left | A \right |}A)A^{*} = E$ ,所以 $(A^{*})^{-1} = \frac{1}{\left | A \right |}A$

六 $A^{*} =\left | A \right |A^{-1}$ 由三转换得六

七 $(A^{*})^{*} = \left | A^{*} \right |(A^{*})^{-1} = \left | A^{} \right |^{n-1}\frac{1}{\left | A \right |}A = \left | A \right |^{n-2}A$

计算过程：

$A^{}A^{*} = \begin{pmatrix} a_{11} &a_{12} & ...& a_{1n}\\ a_{21} & a_{22}& ...& a_{2n}\\ ...& ...& ...&... \\ a_{n1}&a_{n2} & ...&a_{nn}\end{pmatrix}$ $\begin{pmatrix} A_{11} &A_{21} & ...& A_{n1}\\ A_{12}& A_{22} & & A_{n2}\\ ... & ...& & ...\\ A_{1n} &A_{2n} & & A_{nn} \end{pmatrix}=$ $\begin{pmatrix} a_{11}A_{11}+a_{12}A_{12}+...+a_{1n}A_{1n} & .... &... & ...\\ ... &... & ...&... \\ ... & ...& ... & ...\\ ...&... &... &... \end{pmatrix}=\begin{pmatrix} \left | A \right | &0 & 0 & 0\\ 0 &\left | A \right | & 0&0 \\ 0 & 0& \left | A \right | &0 \\ 0 &0 &0 &\left | A \right | \end{pmatrix} = \left | A^{} \right |E$

*矩阵所有元素都有公因子向外提一次，行列式每行或每列有一个公因子向外提一次

*方阵按某一行或按某一列展开再乘以这一行或这一列的代数余子式等于这个矩阵的行列式的值

*异乘变0

按行求，按列放

4.3逆矩阵

定义：A是一个n级的方阵，存在n级方阵B 使得 $A^{}B^{} = B^{}A^{} = E^{}$ , $A^{^{-1}} = B$

1 不是所有方阵都可逆 2 若矩阵可逆，则逆矩阵唯一

如何判断可逆的：

若方阵 $\left | A \right | !=0$ ，那么这个方阵可以叫做（非奇异，非退化，满秩）可逆。

定理1 $A$ 可逆的充要条件 $\left | A \right | !=0$ (这个方阵的行列式的值不为0)

并且 $A^{-1} = \frac{1}{\left | A \right |}A^{*}$

证明 $\bigtriangleup$ 以上公式

因为 $A^{}A^{*} = A^{*}A^{} = \left | A \right |E$ 这个公式同时三个式子同时除以 $\left | A^{} \right |$

$A(\frac{1}{\left | A \right |})A^{*} = ((\frac{1}{\left | A \right |})A^{*} )A = E$

又因为 $A^{}B^{} = B^{}A^{} = E^{}$

$A^{-1} = B$ ,

所以 $A^{-1} = \frac{1}{\left | A \right |}A^{*}$

性质：

一 A可逆， $A^{-1}$ 可逆 $A^{-1^{-1}} =A$

二 $(A)A^{-1} = A^{-1}A = E$

三若AB均可逆，则 $(AB)^{-1} = B^{-1}A^{-1}$

四 A可逆， $A^{T}$ 可逆则

五六性质

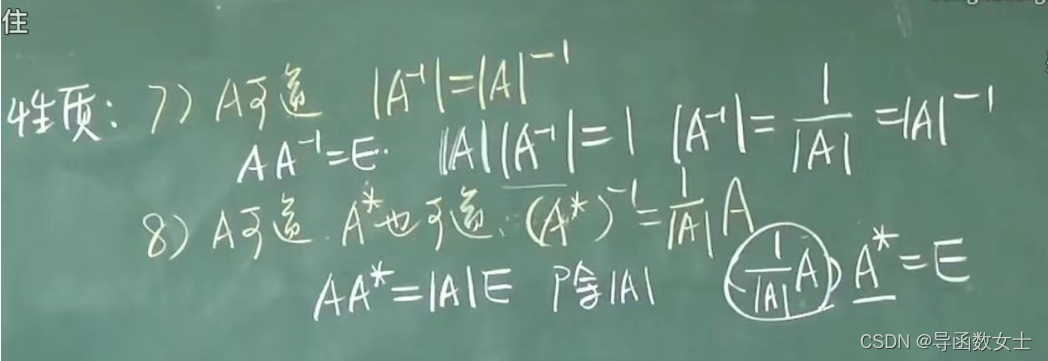
五.分块矩阵

5.1 标准形

5.2 分块矩阵加法、数乘、乘法注意乘法需要矩阵同型

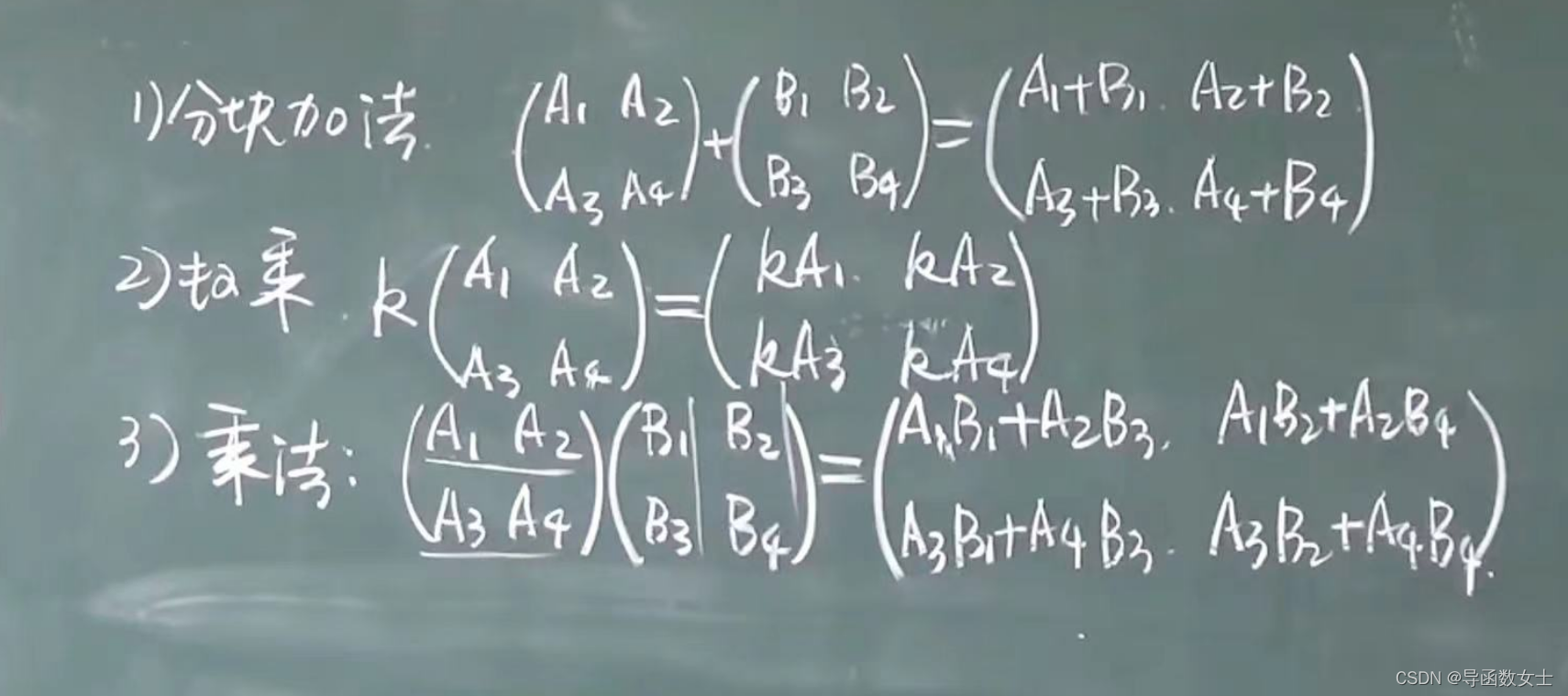
5.3 分块矩阵转置

第一步，把子块视作普通元素求转置，第二步，子块求转置

$A = \begin{pmatrix} A &B &C \\ D&E &F \end{pmatrix}$ $A^{T} = \begin{pmatrix} A^{T} &D^{T} \\ B^{T} & E^{T} \\ C^{T} & F^{T} \end{pmatrix}$

利用拉普拉斯k阶行列式求 $H$ 的逆矩阵。

$A = \begin{pmatrix} A & & \\ &B & \\ & &C \end{pmatrix}$ $,A^{-1}= \begin{pmatrix} A^{-1} & & \\ &B^{-1} & \\ & & C^{-1} \end{pmatrix}$

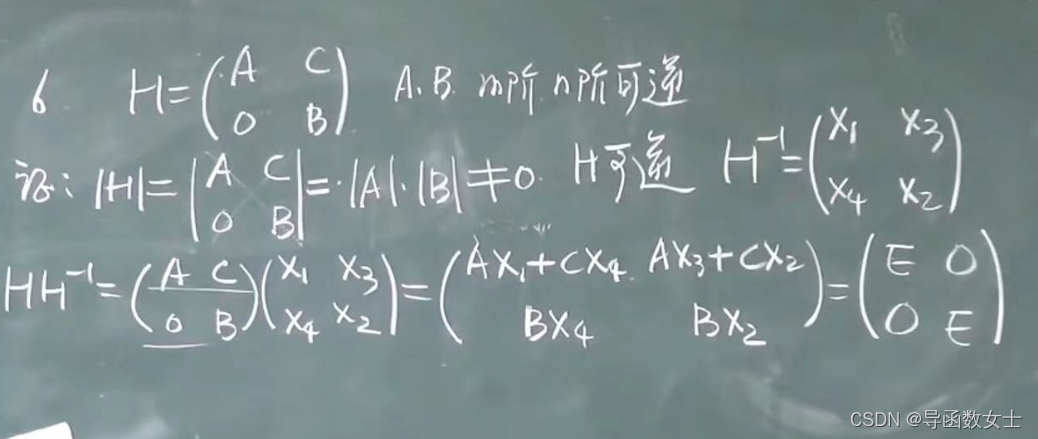
5.4 总结：矩阵的初等变换：行列

5.6 区分矩阵和行列式初等变化的区别：

矩阵：强调矩阵的变化行列式：强调行列式的值

1交换两行 1 行列式交换2行，行列式要变号

2用k乘以某一行 k!=0 2 K 乘以某一行，等于用k乘以这个行列式

3 某一行的L倍加到另一行上去 3 某一行 L倍，加到另一行上去，行列式的值D不变

5.7 分块矩阵定理：

任意矩阵都可以通过初等行变换变成标准型

等价性：反身性，对称性传递性

任意矩阵都等于标准型

5.8 初等方阵

定义：对E做一次初等变换行/列得到的矩阵叫初等方阵。

1 交换2列

$E = \begin{pmatrix} 1 & & & \\ &1 & & \\ & &1 & \\ & & &1 \end{pmatrix}$ 换2列 $\begin{pmatrix} & & 1& \\ & 1& & \\ 1& & & \\ & & &1 \end{pmatrix}$ 叫做 $E(i,j)$ ,

交换后的行列式是 $\begin{vmatrix} & &1 & \\ &1 & & \\ 1& & & \\ & & &1 \end{vmatrix}$ $值为：$ $\left | E(i,j)) \right | =-1$ 交换后的逆矩阵是 $E^{-1} =E(i,j)$

2 用k乘( k！= 0)乘以某行

$E = \begin{pmatrix} 1 & & & \\ &1 & & \\ & &1 & \\ & & &1 \end{pmatrix}$ k =5 $\begin{pmatrix} 1 & & & \\ &1 & & \\ & & 5 & \\ & & & 1 \end{pmatrix}$ 叫做 $E(i(k))$

交换后的行列式 $\begin{vmatrix} 1 & & & \\ &1 & & \\ & &5 & \\ & & &1 \end{vmatrix}$ 值为： $\left | E(i(k)) \right | =K,(K!=0)$ 交换后的逆矩阵是 $E^{-1} = E(i(\frac{1}{K}))$

3 某行的L倍加到另一行上去

$E = \begin{pmatrix} 1 & & & \\ &1 & & \\ & &1 & \\ & & &1 \end{pmatrix}$ 第三行的五倍加到一行上去 $\begin{pmatrix} 1 & &5 & \\ & 1& & \\ & &1 & \\ & & &1 \end{pmatrix}$ 叫做 $E(i(LK))$