前言
在算法学习的过程中,动态规划(Dynamic Programming, DP)和并查集(Union-Find)是两种非常重要且常用的算法技巧。它们能够帮助我们解决很多复杂的问题,尤其是在面对大规模数据时,能够显著提高算法的效率。
包子凑数
小明几乎每天早晨都会在一家包子铺吃早餐。
他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 Ai个包子。
每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。
比如一共有 3 种蒸笼,分别能放 3、4 和 5 个包子。
当顾客想买 11 个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1 笼 3 个的再加 2 笼 4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。
比如一共有 3 种蒸笼,分别能放 4、5 和 6 个包子。
而顾客想买 7 个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入格式
第一行包含一个整数 N。
接下来 N 行,每行包含一个整数 Ai。
输出格式
输出一个整数代表答案。
如果凑不出的数目有无限多个,输出INF。
数据范围
1≤N≤100,
1≤Ai≤100
输入样例1:
2
4
5
输出样例1:
6
输入样例2:
2
4
6
输出样例2:
INF
样例解释
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
算法思路
这道题思路跟完全背包类似(动态规划完全背包问题-java)
一个二维布尔类型数组dp :dp[i][j] 表示是否可以通过前 i 个蒸笼的组合能否得到 j个包子true为可组成该数j,false为不能构成。
整型数组arr:用来存储每个蒸笼所包含的包子个数
求有多少种数目是各个蒸笼的包子组合不出来的,其实就是求各个蒸笼的包子的最大公因数,当最大公因数不为1的时候,此时不能组成的数目个数是无穷多个,当最大公因数为1的时候,此时不能组成的数目个数是有限个的。
用辗转相除法求最大公因数gcd函数如下:(试除法求约数+辗转相除法求最大公约数-java)
//最大公约数
public static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
集合分析法:由最后不同的一步来划分集合,在重量为j的时候,第i集合分析法:
由最后不同的一步来划分集合,在重量为𝑗的时候,第𝑖个物品选了几件。dp(i,j)=dp(i−1,j)||dp(i−1,j−w(i))||…||dp(i−1,j−k∗w(i))(k=j/w(i))𝑑𝑝(𝑖,𝑗)=𝑑𝑝(𝑖−1,𝑗)||𝑑𝑝(𝑖−1,𝑗−𝑤(𝑖))||…||𝑑𝑝(𝑖−1,𝑗−𝑘∗𝑤(𝑖))(𝑘=𝑗/𝑤(𝑖))
但是,完全背包问题有个特殊的地方:那就是 状态重叠 :
dp(i,j−w(i))是由dp(i−1,j−w(i))||dp(i−1,j−2∗w(i))…||dp(i−1,j−k∗w(i) (k=j/w(i))
𝑑𝑝(𝑖,𝑗−𝑤(𝑖))是由𝑑𝑝(𝑖−1,𝑗−𝑤(𝑖))||𝑑𝑝(𝑖−1,𝑗−2∗𝑤(𝑖))…||𝑑𝑝(𝑖−1,𝑗−𝑘∗𝑤(𝑖))(𝑘=𝑗/𝑤(𝑖))
转移过来,仔细看上下两个式子就会发现dp(i,j−w(i))的状态就是dp(i,j)后面一大部分。𝑑𝑝(𝑖,𝑗−𝑤(𝑖))的状态就是𝑑𝑝(𝑖,𝑗)后面一大部分。
所以最终方程为:dp(i,j)=dp(i−1,j)||dp(i,j−w(i))(w(i)≤j)
代码如下
import java.io.*;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 10010;
static int[] arr = new int[N];
static boolean[][] dp = new boolean[110][N];
public static void main(String[] args)throws Exception {
int n = nextInt();
int d = 0;
for(int i = 1;i <= n;i++){
arr[i] = nextInt();
d = gcd(arr[i],d);
}
if(d != 1){
pw.println("INF");
pw.flush();
return;
}
dp[0][0] = true;
for(int i = 1;i <= n;i++){
for(int j = 0;j < N;j++){
dp[i][j] = dp[i-1][j];
if(j >= arr[i]){
dp[i][j] |= dp[i][j-arr[i]] ;
}
}
}
int res = 0;
for(int i = 0;i < N;i++){
if(!dp[n][i]){
res++;
}
}
pw.println(res);
pw.flush();
}
//最大公约数
public static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
}
括号配对
Hecy 又接了个新任务:BE 处理。
BE 中有一类被称为 GBE。
以下是 GBE 的定义:
空表达式是 GBE
如果表达式 A 是 GBE,则 [A] 与 (A) 都是 GBE
如果 A 与 B 都是 GBE,那么 AB 是 GBE
下面给出一个 BE,求至少添加多少字符能使这个 BE 成为 GBE。
注意:BE 是一个仅由(、)、[、]四种字符中的若干种构成的字符串。
输入格式
输入仅一行,为字符串 BE。
输出格式
输出仅一个整数,表示增加的最少字符数。
数据范围
对于所有输入字符串,其长度小于100。
输入样例:
[])
输出样例:
1
算法思路
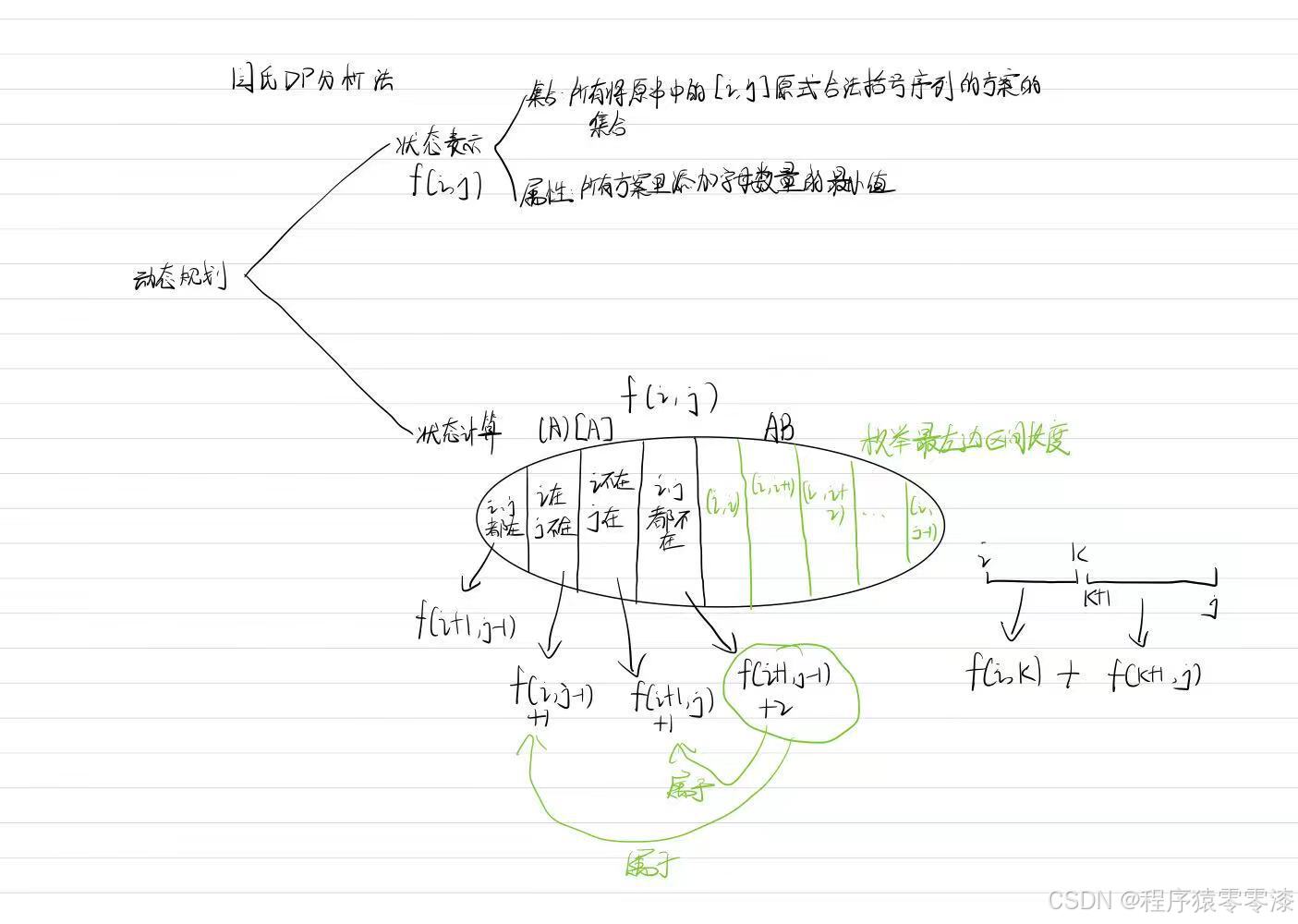
使用二维数组 f[i][j] 来表示字符串 s 从位置 i 到位置 j 的子串需要的最少插入字符数,使得该子串变成一个合法的括号配对表达式(GBE)。
f[i][i] = 1:单个字符是无效的括号表达式,因此至少需要插入一个字符来使其合法。
f[i][j] 初始设为一个很大的数(1e9),表示没有计算出最优解。
通过遍历字符串的子串长度 len,从小到大进行处理。对于每一个子串 s[i…j],我们尝试计算出最小的插入次数:
-
直接匹配:如果 s[i] 和 s[j] 是一对匹配的括号(( 与 ),或 [ 与 ]),那么这个子串在不插入任何字符的情况下就已经是合法的。此时 f[i][j] = f[i + 1][j - 1]。
-
不匹配时的处理:如果 s[i] 和 s[j] 不匹配,我们尝试通过删除一个括号或者插入一个字符来使其合法。两种选择分别是:
- 计算 f[i][j-1] 和 f[i+1][j],并加 1,表示将某个字符删除或插入。其中左右边界都不在f[i+1][j-1]+2包含在f[i][j-1]+1或 f[i+1][j]+1情况之内
- 尝试通过分割子串来解决子问题,分割点为 k,所以 f[i][j] = Math.min(f[i][j], f[i][k] + f[k+1][j])。
最终,f[0][n-1] 就是整个字符串从 0 到 n-1 变成合法括号配对表达式所需的最少插入字符数。
is_match:判断是否是一对有效的括号。
两重循环:外循环是遍历子串的长度,内循环是遍历每个子串的位置左边界,计算该子串的最小插入字符数。
代码如下
package AcWingLanQiao;
import java.io.*;
public class 括号配对 {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 110;
static int[][] f = new int[N][N];
static int n;
public static void main(String[] args)throws Exception {
String s = nextLine();
n = s.length();
//初始化DP表,所有一字符子串需要1个字符来补充合法
for (int i = 0; i < n; i ++ ){
f[i][i] = 1;
}
for(int len = 2; len <= n; len++) {
for(int i = 0; i + len - 1 < n; i++) {
int j = i + len - 1;
f[i][j] = (int)1e9;
if(is_match(s.charAt(i),s.charAt(j))) {
f[i][j] = f[i + 1][j - 1];
}
f[i][j] = Math.min(f[i][j], Math.min(f[i][j-1], f[i + 1][j]) + 1);
for(int k = i;k < j; k++) {
f[i][j] = Math.min(f[i][j], f[i][k]+f[k+1][j]);
}
}
}
pw.println(f[0][n-1]);
pw.flush();
}
public static boolean is_match(char l, char r) {
if(l == '(' && r == ')') {
return true;
}
if(l == '[' && r == ']') {
return true;
}
return false;
}
public static String nextLine() throws Exception {
return br.readLine();
}
}
修改数组
给定一个长度为 N 的数组 A=[A1,A2,⋅⋅⋅AN],数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。
小明会依次修改 A2,A3,⋅⋅⋅,AN。
当修改 Ai 时,小明会检查 Ai 是否在 A1∼Ai−1 中出现过。
如果出现过,则小明会给 Ai 加上 1;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1,直到 Ai 没有在 A1∼Ai−1 中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
现在给定初始的 A 数组,请你计算出最终的 A 数组。
输入格式
第一行包含一个整数 N。
第二行包含 N 个整数 A1,A2,⋅⋅⋅,AN。
输出格式
输出 N 个整数,依次是最终的 A1,A2,⋅⋅⋅,AN。
数据范围
1≤N≤105,
1≤Ai≤106
输入样例:
5
2 1 1 3 4
输出样例:
2 1 3 4 5
算法思路

主要采用并查集的方法来处理。
初始化并查集数组 p[]:每个元素 i 初始化时 p[i] = i,当p[i] = i时,就说明此时该位还未被访问。
p[i]:表示i所在结点的下一个结点
find(x):找到x向右第一个没有被访问过的点
public static int find(int x){
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
对于输入的每个元素 x:
调用 find(x) 查找 x向右第一个没被使用的元素
然后,通过 p[x] = p[x] + 1 增加这个元素的大小,此时就是新数组修改后的元素大小。
代码如下
import java.io.*;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 1100010;
static int[] p = new int[N];
static int n;
public static void main(String[] args)throws Exception {
n = nextInt();
for(int i = 1;i < N;i++){
p[i] = i;
}
for(int i = 1; i <= n; i++){
int x = nextInt();
x = find(x);
pw.print(x+" ");
p[x] = p[x] + 1;
}
pw.flush();
}
public static int find(int x){
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
}
总结
通过本文的学习,我们深入了解了动态规划和并查集这两种基础算法技巧及其应用。在处理包子凑数和括号匹配问题时,动态规划通过将大问题分解为子问题,帮助我们高效地找到最优解。我们还讨论了并查集在处理数组修改问题时的应用,它通过高效的集合管理操作,确保了在大规模数据下依然能保持较高的时间效率。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








