前言
在本博客中,我们将通过动态规划这一强大的算法工具,探讨如何高效解决一些经典问题,如糖果分配问题、密码脱落问题以及生命之树问题。动态规划(DP)是一种将复杂问题分解为更小子问题并利用已有的解来避免重复计算的算法策略。这些问题不仅在实际应用中具有广泛的意义,同时也能帮助我们更好地理解和应用动态规划的思想。
糖果
由于在维护世界和平的事务中做出巨大贡献,Dzx被赠予糖果公司2010年5月23日当天无限量糖果免费优惠券。
在这一天,Dzx可以从糖果公司的 N件产品中任意选择若干件带回家享用。
糖果公司的 N 件产品每件都包含数量不同的糖果。
Dzx希望他选择的产品包含的糖果总数是 K 的整数倍,这样他才能平均地将糖果分给帮助他维护世界和平的伙伴们。
当然,在满足这一条件的基础上,糖果总数越多越好。
Dzx最多能带走多少糖果呢?
注意:Dzx只能将糖果公司的产品整件带走。
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行 1 个整数,表示糖果公司该件产品中包含的糖果数目,不超过 1000000。
输出格式
符合要求的最多能达到的糖果总数,如果不能达到 K 的倍数这一要求,输出 0。
数据范围
1≤N≤100,
1≤K≤100,
输入样例:
5 7
1
2
3
4
5
输出样例:
14
样例解释
Dzx的选择是2+3+4+5=14,这样糖果总数是7的倍数,并且是总数最多的选择。
算法思路
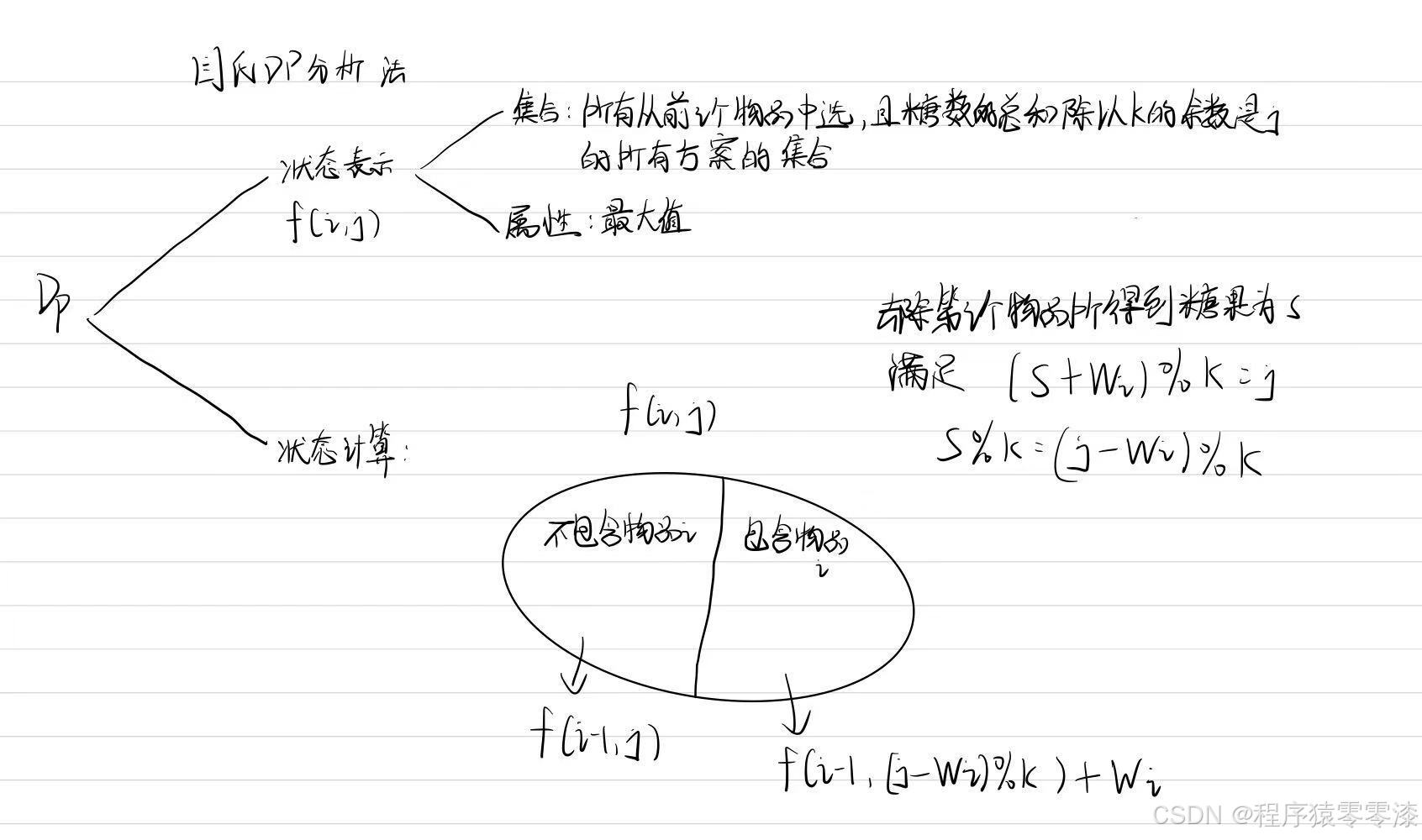
n:商品的数量。
k:要求的总糖果数应当满足的条件(总糖果数对 k 取余为0)。
dp:二维数组,dp[i][j] 表示前 i 个商品中,能够得到总糖果数对 k 取余为 j 的最大糖果数。
边界情况:
- 初始时,dp[0][0] = 0 表示没有商品时,能得到的重量是 0,且 0 % k == 0。
- 其余 dp[0][j] 都初始化为负无穷,表示在没有商品的情况下,其他余数是不可能的。
对于每一个商品的糖果数为 w,进行状态转移:
dp[i][j] 的值是通过比较两种情况得到的:
- 不选当前商品:dp[i-1][j]
- 选当前商品:dp[i-1][(j + k - w % k) % k] + w
这两个情况分别表示:如果不选当前商品,那么当前状态 j 就和前一个状态 j 一样;如果选当前商品,则需要把之前余数为 (j - w ) % k 的状态加上商品的糖果数 w。因为防止出现j - w为负数所以转换为(j + k - w % k) % k。
最终的目标是 dp[n][0],即在考虑所有 n 个商品后,得到一个糖果数对 k 取余为 0 的最大糖果数。
代码如下
import java.io.*;
import java.util.Arrays;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 110;
static int[][] dp = new int[N][N];
static int n,k;
public static void main(String[] args) throws Exception{
n = nextInt();
k = nextInt();
Arrays.fill(dp[0],Integer.MIN_VALUE);
dp[0][0] = 0;
for(int i = 1; i <= n; i++){
int w = nextInt();
for(int j = 0; j < k; j++){
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][(j + k - w % k ) % k] + w);
}
}
pw.println(dp[n][0]);
pw.flush();
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
}
密码脱落
X星球的考古学家发现了一批古代留下来的密码。
这些密码是由A、B、C、D 四种植物的种子串成的序列。
仔细分析发现,这些密码串当初应该是前后对称的(也就是我们说的镜像串)。
由于年代久远,其中许多种子脱落了,因而可能会失去镜像的特征。
你的任务是:
给定一个现在看到的密码串,计算一下从当初的状态,它要至少脱落多少个种子,才可能会变成现在的样子。
输入格式
共一行,包含一个由大写字母ABCD构成的字符串,表示现在看到的密码串。
输出格式
输出一个整数,表示至少脱落了多少个种子。
数据范围
输入字符串长度不超过1000
输入样例1:
算法思路
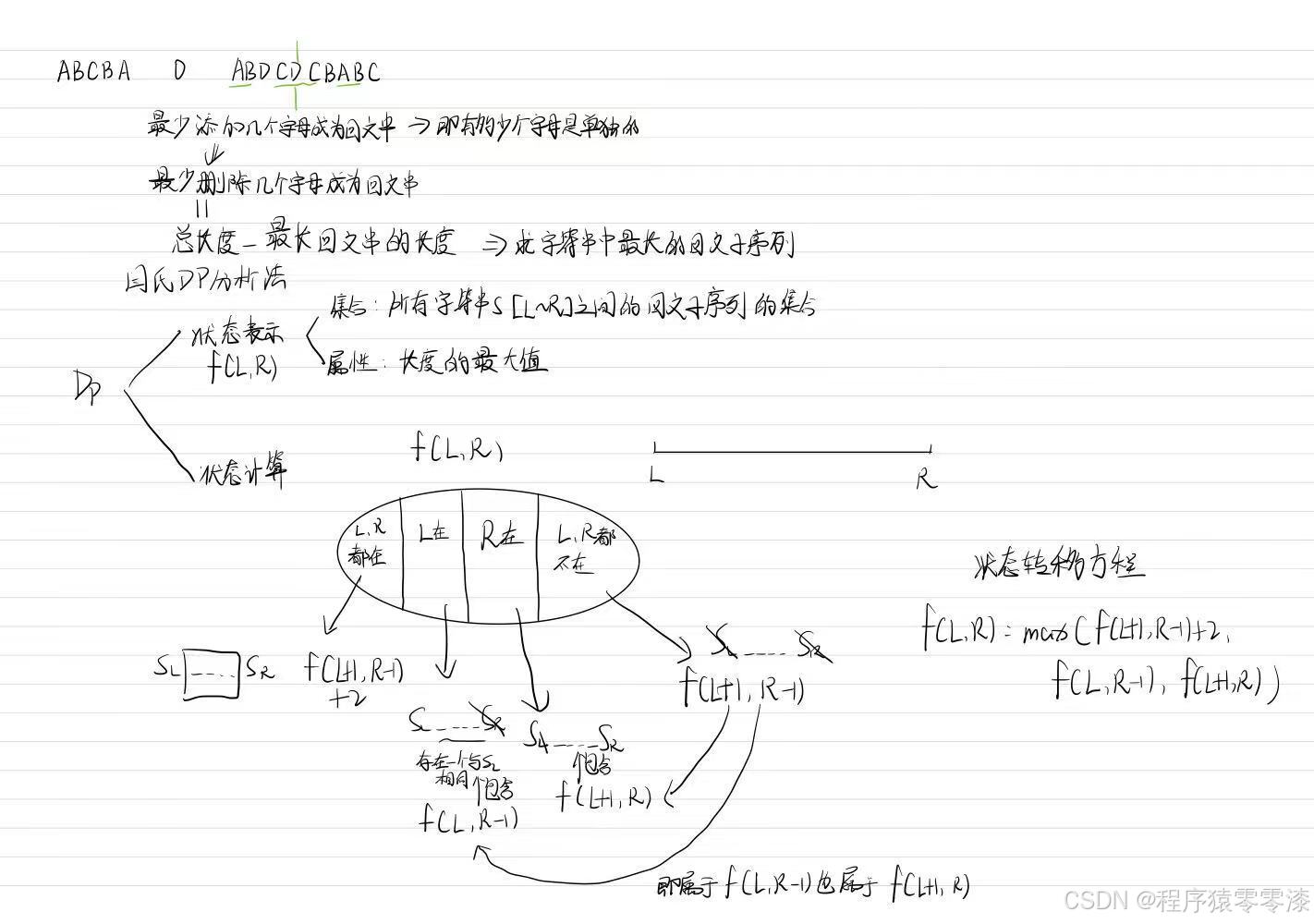
要求删除多少个字母最后的字符串是回文字符串,可以求字符串中的最长回文子序列,然后用字符串的总长度-最长回文子序列就可知道需要删除的最小字母数。
dp[l][r]:表示字符串从l到r的最长回文字符串的长度
arr:字符串数组用来存储字符串
状态属性:
- L、R都在:字符串中的左端点、右端点都属于回文子序列。当然需要一个前提条件 arr[l] == arr[r],中间字符串的最长回文子序列dp[l+1][r-1]加上两个端点即dp[l][r] = dp[l+1][r-1] + 2;
- L、R都不在:字符串中的左端点和右端点都不属于回文子序列,此时字符串的最长回文子序列就是去除两个段点的最长回文子序列即dp[l+1][r-1];
- L在R不在:因为L在R不在。故字符串中的右边需要出现一个与arr[l]相同的字符,但这种情况太多了,我们需要求的是最长回文子序列,可以用dp[l][r-1]来包含L在R不在这种情况;
- R在L不在:因为R在L不在。故字符串中的左边需要出现一个与arr[r]相同的字符,但这种情况太多了,我们需要求的是最长回文子序列,可以用dp[l+1][r]来包含L在R不在这种情况;
i f ( a r r [ l ] = = a r r [ r ] ) d p [ l ] [ r ] = d p [ l + 1 ] [ r − 1 ] + 2 ; d p [ l ] [ r ] = m a x ( d p [ l ] [ r ] , d p [ l ] [ r − 1 ] , d p [ l + 1 ] [ r ] , d p [ l + 1 ] [ r − 1 ] ) ; if(arr[l] == arr[r]) dp[l][r] = dp[l+1][r-1] + 2; \\ dp[l][r] = max(dp[l][r],dp[l][r-1],dp[l+1][r],dp[l+1][r-1]); if(arr[l]==arr[r])dp[l][r]=dp[l+1][r−1]+2;dp[l][r]=max(dp[l][r],dp[l][r−1],dp[l+1][r],dp[l+1][r−1]);
又因为其中dp[l][r-1]是包含dp[l+1][r-1]这一种情况的,因为dp[l][r-1]就是l可选可不选且r一定不选,上述求最大值直接取dp[l][r-1]这种情况即可。
故当arr[l] != arr[r]
d
p
[
l
]
[
r
]
=
m
a
x
(
d
p
[
l
]
[
r
]
,
d
p
[
l
]
[
r
−
1
]
,
d
p
[
l
+
1
]
[
r
]
)
;
dp[l][r] = max(dp[l][r],dp[l][r-1],dp[l+1][r]);
dp[l][r]=max(dp[l][r],dp[l][r−1],dp[l+1][r]);
外部循环: for(int len = 1; len <= n; len++) 遍历所有可能的子串长度。
内部循环: for(int l = 0; l + len - 1 < n; l++) 用来遍历每个子串的起始位置 l,并根据子串的长度计算右端点 r。
输出结果: 最终结果是 n - dp[0][n-1],即最小插入次数。
代码如下
import java.io.*;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 1010;
static char[] arr = new char[N];
static int[][] dp = new int[N][N];
static int n;
public static void main(String[] args)throws Exception {
arr = nextLine().toCharArray();
n = arr.length;
//枚举字符串长度
for(int len = 1; len <= n; len++) {
//枚举左端点
for(int l = 0;l + len - 1 < n; l++) {
//右端点
int r = l + len - 1;
if(len == 1){
dp[l][r] = 1;
}else{
if(arr[l] == arr[r]){
dp[l][r] = dp[l+1][r-1] + 2;
}
dp[l][r] = Math.max(dp[l][r],dp[l+1][r]);
dp[l][r] = Math.max(dp[l][r],dp[l][r-1]);
}
}
}
pw.println(n - dp[0][n-1]);
pw.flush();
}
public static String nextLine()throws Exception{
return br.readLine();
}
}
生命之树
在X森林里,上帝创建了生命之树。
他给每棵树的每个节点(叶子也称为一个节点)上,都标了一个整数,代表这个点的和谐值。
上帝要在这棵树内选出一个非空节点集 S,使得对于 S 中的任意两个点 a,b,都存在一个点列 {a,v1,v2,…,vk,b} 使得这个点列中的每个点都是 S 里面的元素,且序列中相邻两个点间有一条边相连。
在这个前提下,上帝要使得 S 中的点所对应的整数的和尽量大。
这个最大的和就是上帝给生命之树的评分。
经过 atm 的努力,他已经知道了上帝给每棵树上每个节点上的整数。
但是由于 atm 不擅长计算,他不知道怎样有效的求评分。
他需要你为他写一个程序来计算一棵树的分数。
输入格式
第一行一个整数 n 表示这棵树有 n 个节点。
第二行 n 个整数,依次表示每个节点的评分。
接下来 n−1 行,每行 2 个整数 u,v,表示存在一条 u
到 v 的边。
由于这是一棵树,所以是不存在环的。
树的节点编号从 1 到 n。
输出格式
输出一行一个数,表示上帝给这棵树的分数。
数据范围
1≤n≤105,
每个节点的评分的绝对值均不超过 106。
输入样例:
5
1 -2 -3 4 5
4 2
3 1
1 2
2 5
输出样例:
8
算法思路
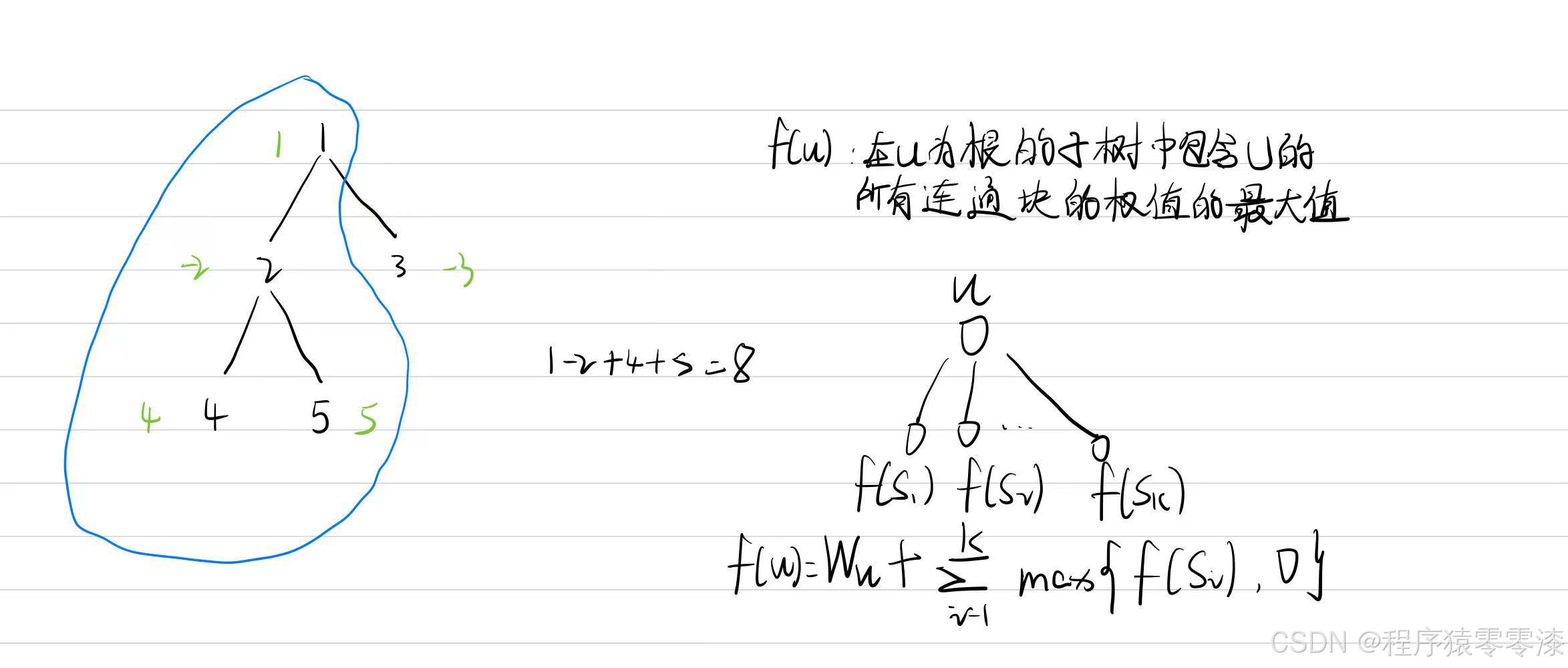
w[i]:用来存储每个点的权值
h[i]:表示图中与i点相连的边有哪些点的单链表
e[i]:模拟单链表中存储的每个结点
ne[i]:表示e[i]这个点在单链表中连接的下一个点
index:表示单链表中即将创建的新结点的下标
f[i]:表示在i为根的子树中包含i的所有连通块的权值的最大值
通过深度优先搜索(DFS)计算一个树结构中,根节点到任意节点路径的最大权值和。每个节点都有一个权值,需要求出经过该节点及其子树的最大路径和。(dfs+动态规划)
采用邻接表存储图,其中用数组来模拟单链表,其中这部分内容可以参考(数组模拟单链表)
dfs(u, father) 函数进行深度优先搜索,其中 u 是当前节点,father 是当前节点的父节点,避免父子节点之间的循环。
DFS递归:
我们通过深度优先搜索(DFS)来遍历整棵树,计算每个节点的最大路径和。DFS的基本流程是:
- 初始化:每个节点的最大路径和初始为节点本身的权值,即 f[u] = w[u]。
- 递归遍历子树:对每个节点 u 的每个子节点 j = e[i],递归地调用 DFS 函数。每次递归
- 调用时,如果子节点的路径和大于0,就将其加到当前节点的路径和中。
- 子树最大值更新:在访问子节点时,若返回的子树路径和为负,则不加,因为负值会减少当前节点的路径和。
对于每个子树,如果其路径和为负值,则不考虑,因为负值会降低当前节点的最大路径和。
DFS遍历完成后,f[i] 数组存储了从根节点到每个节点的最大路径和。我们只需要返回 f[i] 数组中的最大值。就是从根节点到任意节点路径的最大值。
代码如下
import java.io.*;
import java.util.Arrays;
public class Main {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static int N = 100010;
static int M = N * 2;
static int n;
static int[] w = new int[N];
static int[] h = new int[N];
static int[] e = new int[M];
static int[] ne = new int[M];
static int index;
static long[] f = new long[N];
public static void main(String[] args)throws Exception {
n = nextInt();
Arrays.fill(h, -1);
for(int i = 1;i <= n;i++){
w[i] = nextInt();
}
for(int i = 0;i < n - 1;i++){
int a = nextInt();
int b = nextInt();
add(a,b);
add(b,a);
}
dfs(1,-1);
long res = f[1];
for(int i = 2;i <= n;i++){
res = Math.max(res,f[i]);
}
pw.println(res);
pw.flush();
}
public static void add(int a, int b){
e[index] = b;
ne[index] = h[a];
h[a] = index++;
}
public static void dfs(int u,int father){
f[u] = w[u];
for(int i = h[u];i != -1 ;i = ne[i]){
int j = e[i];
if(j != father){
dfs(j,u);
f[u] += Math.max(0,f[j]);
}
}
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
}
总结
通过本博客的讲解,我们深入分析了糖果分配、密码脱落和生命之树这三个问题,并展示了如何使用动态规划来求解它们。通过精妙的状态转移方程和优化技巧,我们能够在复杂问题中找到高效的解法。动态规划的本质在于通过记忆化存储和逐步优化,解决问题的效率得到了极大提升,这使得它成为了许多优化问题中的首选解决方案。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








