合并集合-java_java 集合合并-优快云博客

进行判断两个元素是否在同一个集合，我们只需要分别找出每个元素的集合编号是否在同一个，就可以判断这两个元素是否在同一个集合。我们需要一个while循环，然后看当前结点的编号是否是该集合的编号即p[x] == x。如果该结点不是根节点即p[x] != x，那么我们就让当前结点变成它的父结点，不断地往上来找它的祖宗也就是最后的根节点即x = p[x]。

     //返回x所在集合的编号
    //找x的祖宗结点
    public static int find(int x){
        while(p[x] != x){
           x = p[x]; 
       }
        return x;
    }

其中我们可以进行一个很重要的优化（敲黑板，划重点）：

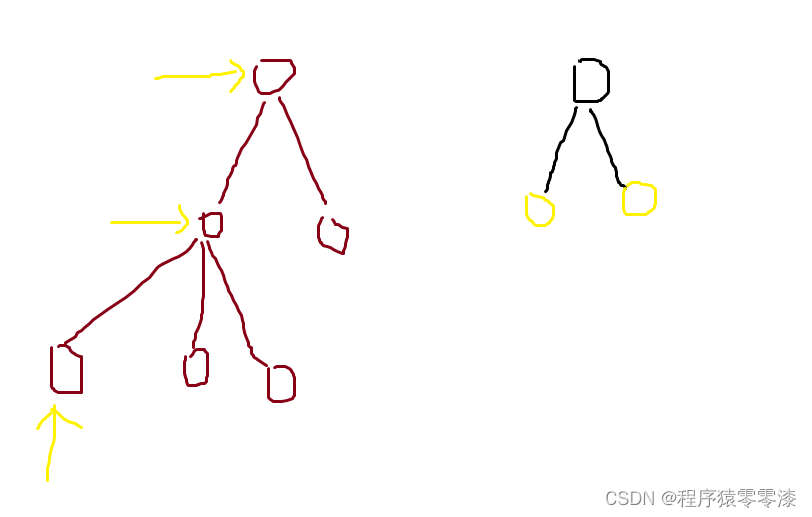
图2.2路径压缩

在我们查找该元素的根节点，我们经历了一个循环，然而这个循环次数是取决于我们的树高，如果我们树只有一个分支并且很长的话那么时间复杂度还是很高。但是我们就可以进行一个优化，在我们找寻该结点所在集合编号的时候，我们可以把同属于一条路径上的所有结点的父结点全部更新为根节点，即图2.2中左边用黄色箭头标识的结点就属于同一路径，这个过程就是路径压缩。

当我们进行路径压缩之后，我们只有第一次处理的时候耗费的时间过程，后面查询元素的的集合编号近似为O(1)的时间复杂度，这是一个对时间很明显的优化。

   //返回x所在集合的编号+路径压缩
    //找x的祖宗结点
    public static int find(int x){
       if(p[x] == x){
           return x;
       }
        return p[x] = find(p[x]);
    }

我们先找到递归的出口，函数的返回值就是递归的出口，最后x就是根节点的编号。 find函数的返回值就是结点x的所在集合的编号即根节点，那么我们传入一个结点x，当此时结点不是根节点的话，我们就把该结点的父结点赋值为所在集合的根节点即 p[x] = find(p[x])，同时我们还把该结点的父结点传入函数，那么我们会不断地找直到找到这条路径上地根节点，然后依次将每一个结点的父结点都赋值为它的根节点。

3.合并两个集合🌙

图2.1合并两个集合示例

我们要合并两个集合的话，我们只需要将一个集合直接挂到另一个集合的任意分支上就可以实现这个操作。例如p[x]是x集合的集合编号，p[y]是y集合的集合编号，那么我们要合并两个集合，把y集合挂到x集合的根节点下面，即p[y] = x就可以实现。

 p[find(y)] = find(x);

p[find(y)]就是结点y的根节点的集合编号的父节点，find(x)就是找到了结点x的根节点的集合编号，然后p[find(y)] = find(x) 就是将x的结点的根节点的集合编号赋值给y结点的根节点的父结点，即将y所在的集合挂到了x结点的所在集合的根节点的下面，完成了两个集合的合并。

三、代码如下☀

1.代码如下：🌙


import java.io.*;
import java.util.*;
public class 合并集合 {
    static PrintWriter  pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static int N = 100010;
    //存储每个元素的父结点是谁
    static int[] p = new int[N];
    public static void main(String[] args) throws Exception{
        Scanner sc = new Scanner(br);
        int n = sc.nextInt();
        int m = sc.nextInt();
        //初始化，有n个点，每一个点就是一个集合，那么就是每一个点的父结点就是自己p[i] = i
        for(int i = 1; i <= n; i++){
            p[i] = i;
        }
        while (m-- > 0){
            String cmd = sc.next();
            int num1 = Integer.parseInt(sc.next());
            int num2 = Integer.parseInt(sc.next());
            if(cmd.equals("M")){
                p[find(num1)] = find(num2);
            } else if (cmd.equals("Q")) {
                int x = find(num1);
                int y = find(num2);
                pw.println( x == y ? "Yes" : "No");
            }
        }
        pw.flush();
    }
     //返回x所在集合的编号+路径压缩
    //找x的祖宗结点
    public static int find(int x){
       if(p[x] == x){
           return x;
       }
        return p[x] = find(p[x]);
    }

}