数据结构—— 树与二叉树

原创已于 2022-03-26 23:23:39 修改 · 1.4k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#java #数据结构

于 2022-03-26 23:20:03 首次发布

本文介绍了树的基本概念和术语，包括结点、度、叶结点等，并详细阐述了二叉树的定义、性质、五种基本形态以及二叉树的顺序和链式存储结构。此外，还探讨了二叉树的前序、中序和后序遍历方法，并提供了Java代码实现。

一、树的定义与基本术语

1、树的基本概念

树是n（n大于等于0）个结点的有限集合。n=0时，称为空树。

2、树的相关术语

（1）结点：包含一个数据元素及若干指向其他结点的分支信息。

（2）结点的度：一个结点的子树个数称为此结点的度。

（3）叶结点：度为0的结点，即无后继的结点，也称为终端结点。

（4）分支结点：度不为0的结点，也称非终端结点。

（5）结点的层次：从根结点开始定义，根结点的层次为1，根的直接后继结点为2，以此类推。

（6）树的度：树中所有节点的度的最大值。

（7）树的深度：树中所有结点层次的最大值。

（8）孩子结点：一个结点的直接后继称为该结点的孩子结点。

（9）双亲结点：一个结点的直接前继称为该结点的双亲结点。

（10）兄弟结点：同一双亲结点的孩子结点之间互称兄弟结点。

（11）森林：m棵互不相交的树的集合。

二、二叉树

1.二叉树的定义：

把满足以下两个条件的树的结构称为二叉树（Binary Tree）：

（1）每个结点的度都不大于2

（2）每个结点的孩子结点次序不能任意颠倒。

二叉树的五种基本形态：

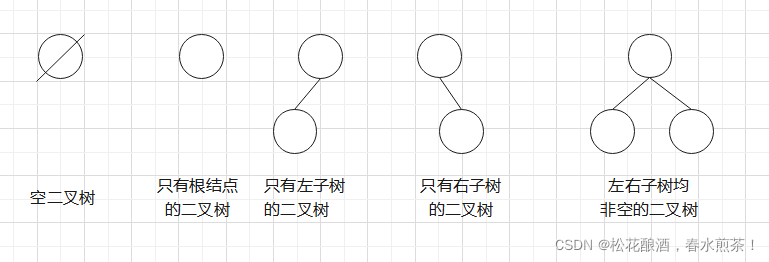
满二叉树：

完全二叉树

2.二叉树的性质：

（1）在二叉树的第i层上最多有2^（i-1）个结点（i大于等于1）。

（2）深度为k的二叉树至多有2^k - 1个结点（k 大于等于 1）。

（3）对任意一棵二叉树T，若终端结点数为n0，而其度数为2的结点数为n2，则 n0 = n2 + 1。

（4）具有n个结点的完全二叉树的深度为（ log 2 n ）+ 1

（5）对于具有n 个结点的完全二叉树,如果按照从上到下和从左到右的顺序对二叉树中的所有结点

从 1 开始顺序编号,则对于任意的序号为 i 的结点有:

①如 i =1,则序号为i的结点是根结点,无双亲结点;如 i>1,则序号为i的结点的双亲结点序号

为i / 2。
②如2i>n,则序号为i的结点无左孩子;如 2i≤n,则序号为i的结点的左孩子结点的序号为2i。

③如2i+1>n,则序号为i的结点无右孩子;如 2i+1≤n,则序号为 i的结点的右孩子结点的序号为

2i+1。

3.二叉树的存储结构

二叉树的结构是非线性的，每个结点最多可有两个后继。二叉树的存储结构有两种：顺序存

储结构和链式存储结构。

（1）顺序存储结构：

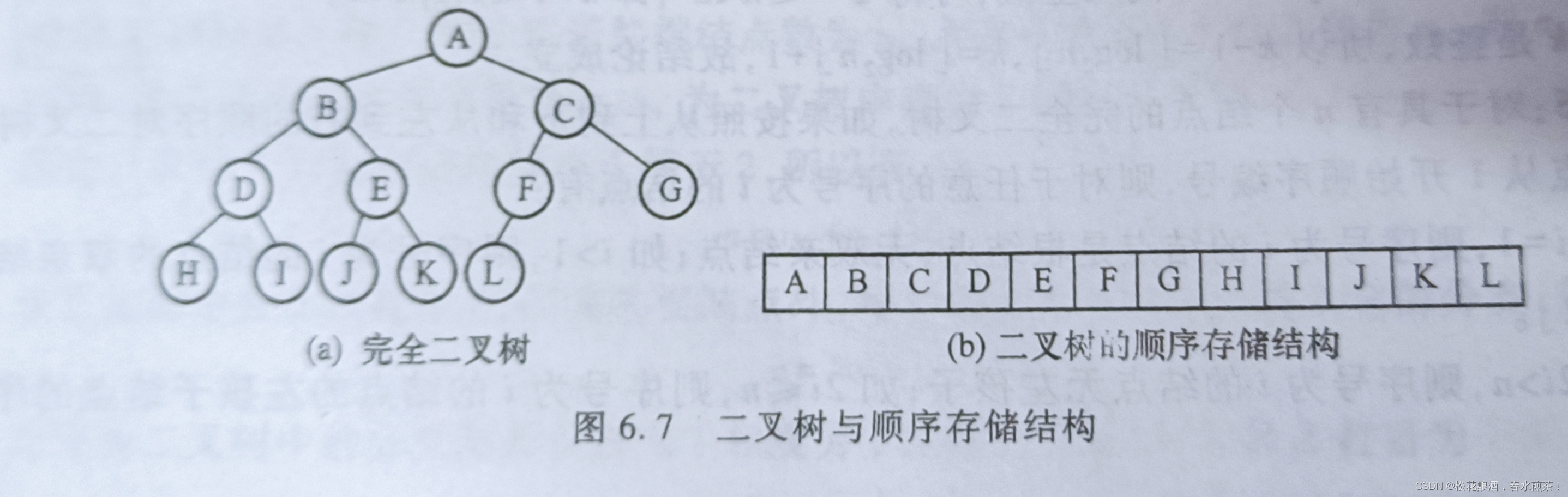
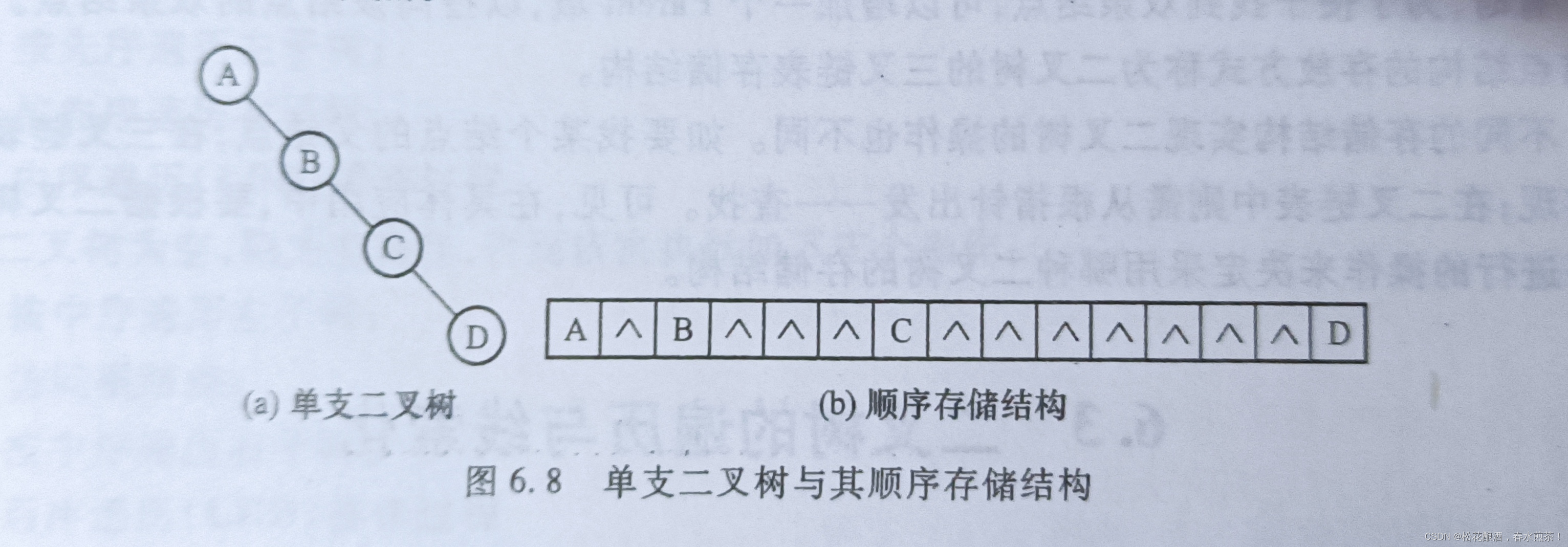
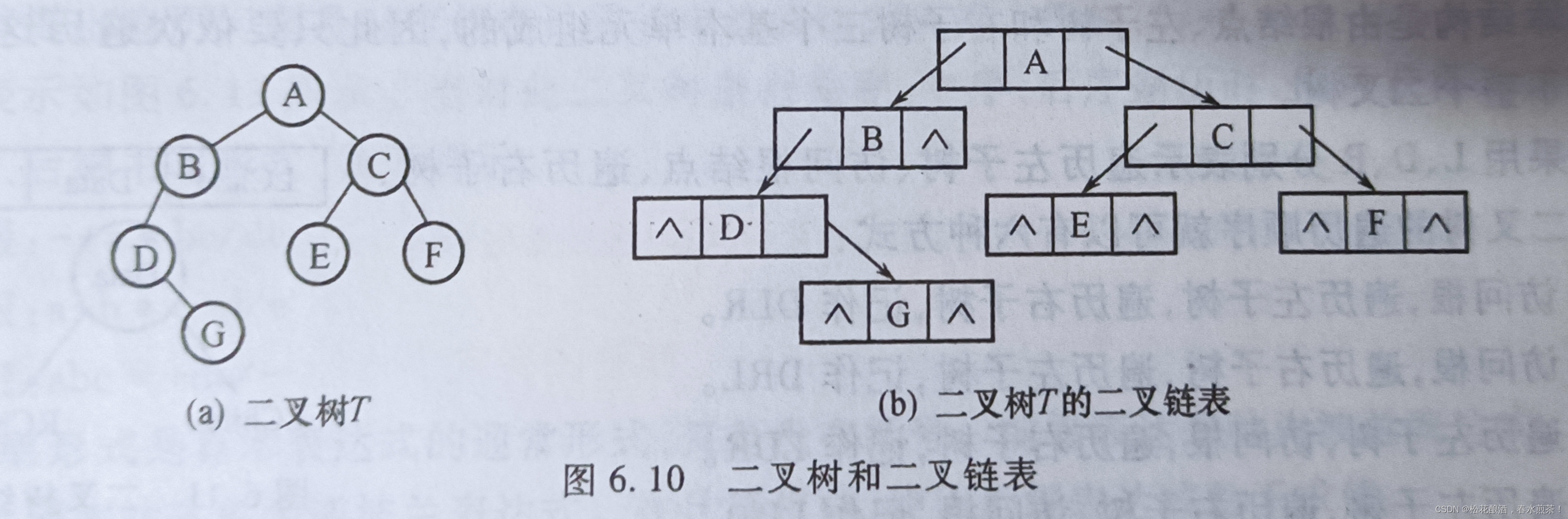
（2）链式存储结构：

对于任意的二叉树来说，每个结点只有一个双亲结点（根除外），最多有两个孩子。可以设计每个结点至少包括三个域：数据域，左孩子域和右孩子域：

结点结构

Lchild

Data

RChild

三、二叉树的遍历

二叉树的遍历是指按一定规律对二叉树的每个结点进行访问且访问一次。其中的访问可指计算二叉树中结点的数据信息，打印该结点的信息，也包括对该结点进行任何其他操作。

下面给出三种遍历方法的递归定义：

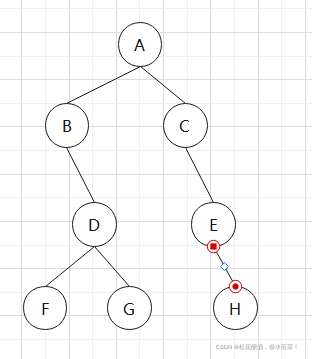
图 1

1、前序遍历（PreOrder）的操作过程

若二叉树为空，则为空操作，否则依次执行如下三个操作：

（1）访问根结点

（2）按先序遍历左子树

（3）按先序遍历右子树

对图 1 进行先序遍历结果如下：A,B,D,F,G,C,E,H

Java代码实现

private static void preOrder(TreeNode root, List<Integer> list) {
        if(root == null){
            return;
        }
        list.add(root.val);
        preOrder(root.left,list);
        preOrder(root.right,list);
    }

2、中序遍历（InOrder）的操作过程

若二叉树为空，则为空操作，否则依次执行如下三个操作：

（1）按中序遍历左子树

（2）访问根结点

（3）按中序遍历右子树

对图 1 进行中序遍历结果如下：B,F,D,G,A,C,E,H

Java代码实现

private static void inOrder(TreeNode root, List<Integer> list) {
        if(root == null){
            return;
        }
        inOrder(root.left,list);
        list.add(root.val);
        inOrder(root.right,list);
    }

3、后序遍历（PostOrder）的操作过程

若二叉树为空，则为空操作，否则依次执行如下三个操作：

（1）按后序遍历左子树

（2）按后序遍历右子树

（3）访问根结点

对图 1 进行后序遍历结果如下：F,G,,D,B,H,E,C,A

Java代码实现

private static void postOrder(TreeNode root, List<Integer> list) {
        if(root == null){
            return;
        }
        postOrder(root.left,list);
        postOrder(root.right,list);
        list.add(root.val);
    }