目录
一.为什么要引入页面置换算法
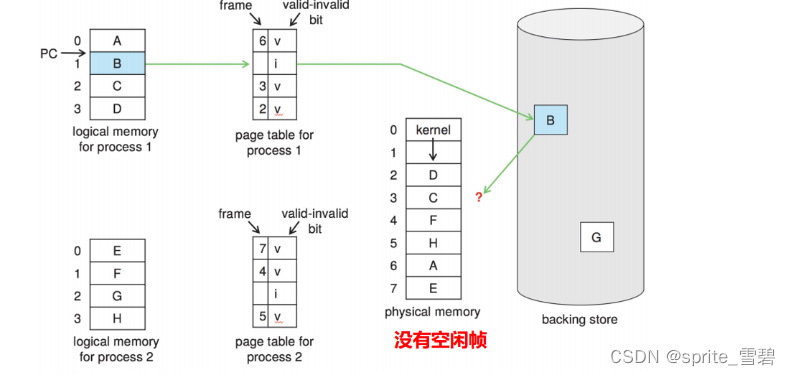
这时,操作系统有多个选项。它可以终止用户进程。然而,请求分页是操作系统试图改善计算机系统的使用率和吞吐量的技术。用户不应该意识到,他们的进程是运行在分页系统上;对用户而言,分页应是透明的。因此,这个选择并不是最佳的。
操作系统可以改为使用标准交换和换出进程,以释放其所有帧并降低多道程度。 然而,由于在内存和交换空间之间复制整个进程的开销,大多数操作系统不再使用标准交换。 大多数操作系统现在将交换页面与页面置换(page replacement)结合在一起。在内存中找到一些页面,但没有真正使用,将其中的页面拿出。
但是我们应该换出内存中的哪个页面呢?
所以我们由此就进入页面置换算法的学习了:

二.页面置换算法
2.1最优页面置换算法
又称为OPT或MIN。置换最长时间不会使用的页面。该算法对于给定数量的页面会产生最低的可能的缺页错误率,不会遭受Belady异常。但难以实现,因为操作系统无法提前预判页面访问序列。因此,最佳置换算法是无法实现的。
例题:
假设系统为某进程分配了三个内存块,并考虑到有一下页面号引用串(会依次访问这些页面):7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1
选择从 0,1,7 中淘汰一 页。按最佳置换的规则, 往后寻找,最后一个出现的页号就是要淘汰的页面。(也就是7)整个过程 缺页中断 发生了 9 次 , 页面置换 发生了 6 次 。注意:缺页时未必发生页面置换。若还有可用的空闲内存块,就不用进行页面置换。缺页率 = 9/20 = 45%
2.2FIFO页面置换算法
每个页面记录了调到内存的时间。当必须置换页面时,将选择最旧的页面。可以创建一个FIFO队列(队列的最大长度取决于系统为进程分配了多少个内存块),来管理所有的内存页面。置换的是队列的首个页面。当调入页面到内存时,就将它加到队列的尾部。每次选择淘汰的页面是最早进入内存的页面
例题:
3个帧(内存块)开始为空。首次的3个引用(7,0,1)会引起缺页错误,并被调到这些空帧。之后将调入这些空闲帧。下一个引用(2)置换7,这是因为页面7最先调入。由于0是下一个引用并且已在内存中,所以这个引用不会有缺页错误。对3的首次引用导致页面0被替代,因为它现在是队列的第一个。因为这个置换,下一个对0的引用将有缺页错误,然后页面1被页面0置换。
2.3LRU页面置换算法
例题:
例:假设系统为某进程分配了 四个 内存块,并考虑到有以下页面号引用串:1, 8, 1, 7, 8, 2, 7, 2, 1, 8, 3, 8, 2, 1, 3, 1, 7, 1, 3, 7
2.4时钟置换算法(CLOCK)(NRU)

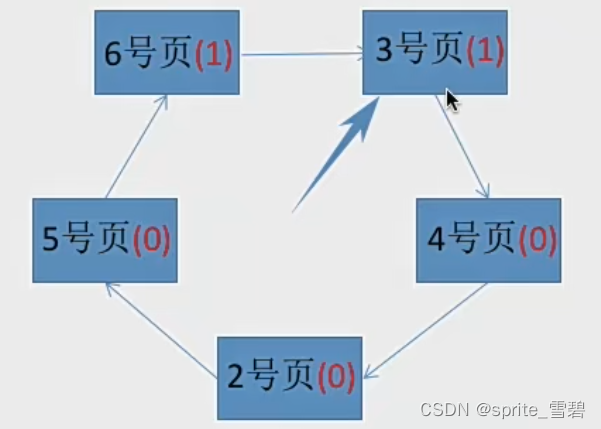
例:假设系统为某进程分配了 五个 内存块,并考虑到有以下页面号引用串:1, 3, 4, 2, 5, 6, 3, 4, 7当访问完五个内存块后,循环队列如下图:
可以看到访问位都为1。
当要引用页面号为6时,发现五个内存块都满了,这时将五个内存块的访问位都设置为0.
然后将页面号为6所需的内容放到1号页占据的内存块:
然后访问3,将3的访问位设置为1。
然后访问4,将4的访问位设置为1.
然后访问7,首先看内存块没有7,然后开始选择替换的页面,指针经过的内存块把访问位设置为0。
找到第一个访问位为0的内存块,替换出去。
基于此就完成了所有任务。
2.5改进的时钟算法
例题1:有下列队列,现在要选择一个页面置换出去。请写出过程。
过程:第一轮扫描,找(0,0)不改变访问位,所以找到了(0,0)然后置换
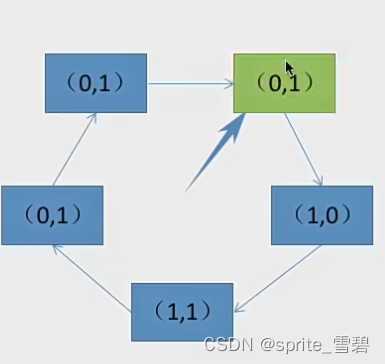
例题2:有下列队列,现在要选择一个页面置换出去。请写出过程。
过程:
第一轮找(0,0)
没有满足情况的。
第二轮扫描,尝试找到(0,1),然后修改扫描过的访问位为0
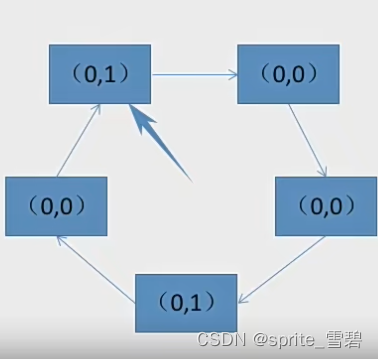
例题3:有下列队列,现在要选择一个页面置换出去。请写出过程。
过程:第一轮找(0,0)不修改访问位,没有发现
第二轮找(0,1)并修改扫描过的访问位为0,没有找到
第三轮找(0,0)不修改访问位,成功找到。




































 1126
1126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








