树与二叉树

最新推荐文章于 2024-06-05 14:49:28 发布

Jamb_n

最新推荐文章于 2024-06-05 14:49:28 发布

阅读量325

点赞数

文章标签： c语言算法

本文链接：https://blog.youkuaiyun.com/m0_62947847/article/details/129413431

版权

3二叉树

3.1二叉树的定义

二叉树是n\geq0个结点的有穷集合D与D上关系的集合R构成的结构，记为T。当n=0时，称T为空二叉树；否则,它为包含了一个根结点以及两棵不相交的、分别称之为左子树与右子树的二叉树。

二叉树的基本形态（五种）

结论:子树有严格的左、右之分且度≤2的树是二叉树。

具有三个结点的二叉树有5种形态，具有三个结点的树有1种形态。

3.2两种特殊形态的二叉树

(129条消息) 二叉树-满二叉树、完全二叉树满二叉树的序号山风wind的博客-优快云博客

1.满二叉树

一棵高度为h，并且含有2^h-1个结点的二叉树称为满二叉树，即树中的每一层都含有最多的结点。满二叉树的叶子节点都集中在二叉树的最下一层，并且除叶子结点之外的每个结点度数均为2.(二叉树结点的度即为结点的孩子个数)。

特点：

\lceil x \rceil

\lfloor x \rfloor

只有最后一层有叶子结点。

不存在度为1的结点

按层序从1开始编号，自上而下，自左向右。这样每个结点对应一个编号，对于编号为i的结点，如果有双亲，其双亲为\lfloor i/2\rfloor，如果有左孩子，则左孩子为2i，如果有右孩子，则有孩子为2i+1。

2.完全二叉树

若一棵二叉树中只有最下面两层的结点的度可以小于2,并且最下面一层的结点(叶结点)都依次排列在该层从左至右的位置上.这样的二叉树为完全二叉树。

设一个高度为h，有n个结点的二叉树，当且仅当其每一个结点都与高度为h的满二叉树中编号为1...n的节点一一对应时，称为完全二叉树。

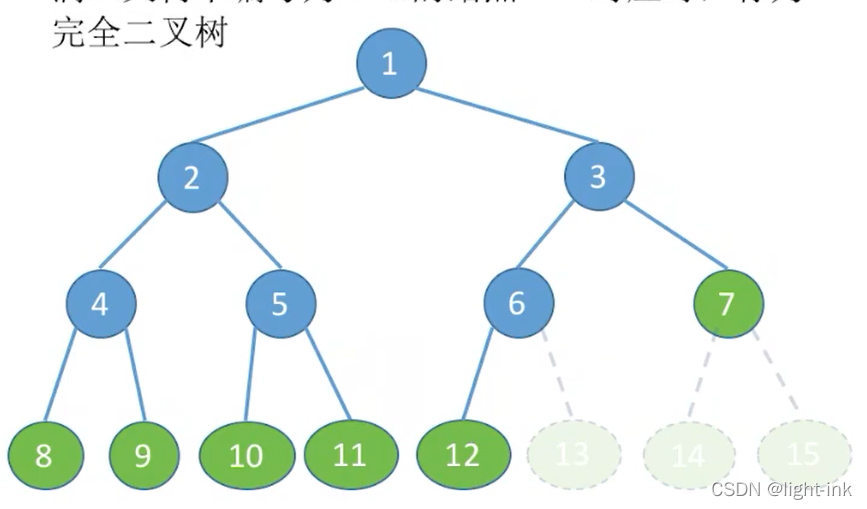
特点：

只有最后两层可能有叶子结点

最多只有一个度为1的结点，且该节点只有左孩子没有右孩子。

若i<=\lfloor n/2 \rfloor，则结点i为分支结点，否则为叶子结点

按层序编号之后，一旦出现某节点（其编号为i）为叶子结点或只有左孩子，那么编号大于i的节点均为叶子结点。

若n为奇数，则每个分支结点都有左孩子和右孩子；若n为偶数，则编号最大的分支结点（编号为n/2）只有左孩子没有右孩子，其余分支结点左右孩子都有。

3.3二叉树的性质

1.具有n个结点的非空二叉树共有n-1个分支

2.非空二叉树的第i层最多有2^{i-1}个结点。i\geq1

3.深度为h的非空二叉树最多有2^h-1个结点。

1+2^1+2^2+...+2^{h-1}=

深度为h的完全二叉树至少有2^{h-1}个结点

4.若非空二叉树有n_0个叶结点，有n_2个度为2的结点，则n_0=n_2+1

证明：n=n_0+n_1+n_2，二叉树的分支数目B=n-1=n_1+n_2

故：n_0=n_2+1

具有n个结点的非空二叉树的深度为h=\lfloor log_2n \rfloor+1

具有n个结点的二叉树的最小深度是多少

6.若对具有n个结点的完全二叉树按照层次从上到下,每层从左到右的顺序进行编号, 则编号为i的结点具有以下性质:

(1)当i=1,则编号为i的结点为二叉树的根结点；

若i>1,则编号为i 的结点的双亲的编号为\lfloor i/2 \rfloor；

(2)若2i>n,则编号为i 的结点无左子树;

若2i<=n,则编号为i 的结点的左孩子的编号为2i；

(3)若2i+1>n,则编号为i 的结点无右子树;

若2i+1>=n,则编号为i 的结点的右孩子的编号为2i+1。

3.5二叉树与树，森林之间的转换

1)树转二叉树

步骤：

(1)加线：在所有相邻的兄弟结点之间分别加一条连线；

(2)抹线：就是对树中的每个结点，只保留他与第一个孩子结点之间的连线，删除它与其它孩子结点之间的连线；

(3)旋转：就是以树的根结点为轴心，将整棵树顺时针旋转一定角度，使之结构层次分明。

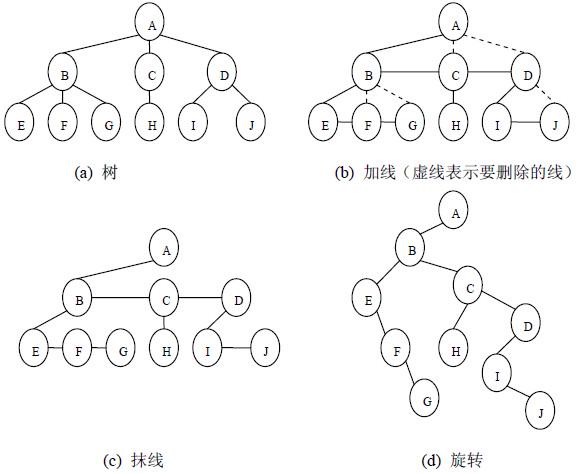
2）二叉树转树

步骤：

(1)若某结点的左孩子结点存在，将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点，将该结点与这些右孩子结点用线连接起来；

(2)删除原二叉树中所有结点与其右孩子结点的连线；

(3)整理（1）和（2）两步得到的树，使之结构层次分明。

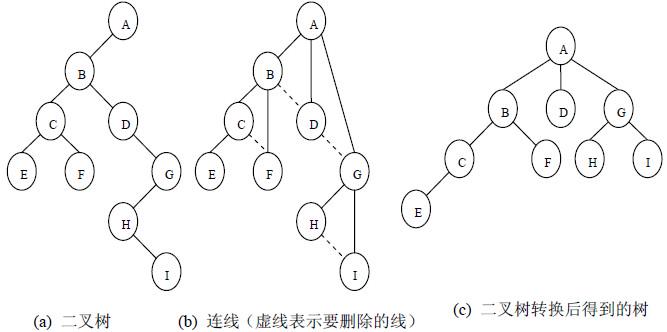
3)森林转二叉树

步骤：

(1)将森林中的每棵树转化成相应的二叉树

(2)第一颗二叉树不动，从第二颗树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子结点，直到所有二叉树都连接到一起

4二叉树的存储结构

4.1二叉树的顺序存储结构

1)完全二叉树的顺序存储结构

根据完全二叉树的性质6 ,对于深度为h的完全二叉树, 将树中所有结点的数据信息按照编号的顺序依次存储到一维数组BT[0..2h-2]中,由于编号与数组下标一一对应，该数组就是该完全二叉树的顺序存储结构。

2)一般二叉树的顺序存储结构

结论：顺序存储结构比较适合满二叉树，或者接近于满二叉树的完全二叉树，对于一些称为退化二叉树的二叉树,顺序存储结构的空间开销浪费的缺点表现比较突出。

4.2二叉树的链式存储结构

1）二叉链表

链结点的构造为：lchild-data-rchild

其中，data为数据域，lchild与rchild分别为指向左，右子树的指针域

2）三叉链表

链结点的构造为：lchild-data-rchild-parent

5二叉树的遍历

5.1常用的遍历方法

1.前序遍历 2.中序遍历 3.后序遍历 4.层次遍历

5.2前序遍历

原则：若被遍历的二叉树非空，则

访问根节点

前序遍历根节点的左子树

前序遍历根节点的右子树

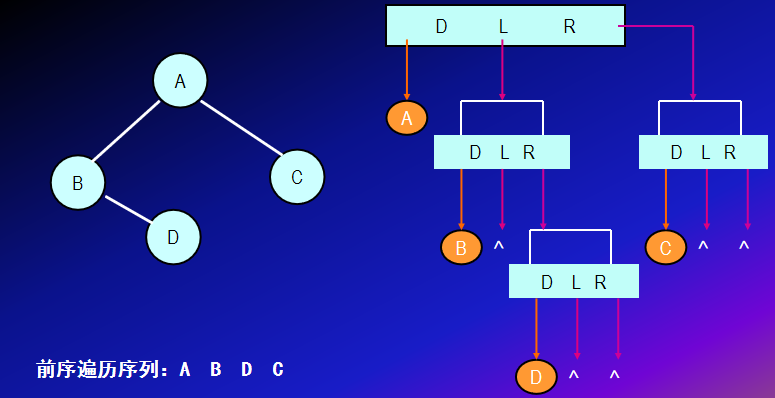
void preorder(BTNodeptr t)
{
    if(t != NULL)
    {
        visit(t);    //访问t指的结点
        preorder(t->lchild);
        preorder(t->rchild);
    }
}

5.3中序遍历

原则：若被遍历的二叉树非空，则

中序遍历根节点的左子树

访问根节点

中序遍历根节点的右子树

void inorder(BTNodeptr t)
{
    if (t != NULL)
    {
        inorder(t->lchild);
        visit(t);   //访问t指的结点
        inorder(t->rchild);
    }
}

5.4后序遍历

原则：若被遍历的二叉树非空，则

后序遍历根节点的左子树

后序遍历根节点的右子树

访问根结点

void postorder(BTNodeptr T)
{
    if (t != NULL)
    {
        postorder(t->lchild);
        postorder(t->rchild);
        visit(t);   //访问t指的结点
    }
}

5.5层次遍历

void layerOrder(BTNodeptr t)
{//O(n)
    BTNodeptr q[N], p;
    int ss = 0, tt = -1;
    
    if (t != NULL)
    {
        q[ ++ tt] = t;
        
        while (ss <= tt)
        {
            p = q[ss ++ ];
            visit(p);
            if (p->lchild != NULL)
                q[ ++ tt] = p->lchild;
            if (p->rchild != NULL)
                q[ ++ tt] = p->rchild;
        }
    }
}

重建二叉树

#include<stdio.h>

#define N 1000100

typedef struct TreeNode{
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
}Node, *Nodeptr;

int pre[N], in[N];
int hash[N];
int n, idx;
int ans[N];

Nodeptr build(int pl, int pr, int il, int ir)
{
    if (pl > pr) return NULL;
    
    Nodeptr root = (Nodeptr)malloc(sizeof(Node));
    
    root->val = pre[pl];
    
    int i = hash[pre[pl]];
    
    root->left = build(pl + 1, pl + i - il, il, i - 1);
    root->right = build(pl + i - il + 1, pr, i + 1, ir);
    
    return root;
}

void postOrder(Nodeptr root)
{
    if(!root) return;
    
    postOrder(root->left);
    postOrder(root->right);
    ans[idx ++ ] = root->val;
}

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++ ) scanf("%d", &pre[i]);
    for (int i = 0; i < n; i ++ )
    {
        scanf("%d", &in[i]);
        hash[in[i]] = i;
    }
    
    Nodeptr tree;
    
    tree = build(0, n - 1, 0, n - 1);
    
    
    postOrder(tree);
    
    printf("%d\n", ans[0]);
    
    return 0;
    
}

树的遍历

#include<stdio.h>

#define N 100010

typedef struct TreeNode{
    int val;
    struct TreeNode* left;
    struct TreeNode* right;
}Node, *Nodeptr;

int pos[N], in[N];
int hash[N];
int n, idx;

Nodeptr build(int pl, int pr, int il, int ir)
{
    if (pl > pr) return NULL;
    
    Nodeptr root = (Nodeptr)malloc(sizeof(Node));
    
    root->val = pos[pr];
    
    int i = hash[pos[pr]];
    
    root->left = build(pl, pl + i - il - 1, il, i - 1);
    root->right = build(pl + i - il, pr - 1, i + 1, ir);
    
    return root;
}

Nodeptr q[1001];
int hh, tt = -1;
void bfs(Nodeptr root)
{
    q[ ++ tt ] = root;
    while (hh <= tt)
    {
        Nodeptr t = q[hh ++ ];
        printf("%d ", t->val);
        if (t->left != NULL ) q[ ++ tt ] = t->left;
        if (t->right != NULL ) q[ ++ tt ] = t->right;
    }
}

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++ ) scanf("%d", &pos[i]);
    for (int i = 0; i < n; i ++ )
    {
        scanf("%d", &in[i]);
        hash[in[i]] = i;
    }
    
    Nodeptr tree;
    
    tree = build(0, n - 1, 0, n - 1);
    
    bfs(tree);
    
    return 0;
    
}

最重要的地方：

队列：

//二叉树结点的类型为：Nodeptr *root;
//那么建立的队列就应该为：
Nodeptr q[N];
int hh = 0, tt = -1;

二叉查找树

有序顺序表(数组)：查找效率高，插入和删除操作效率低

有序链表：删除和插入操作效率高，链式存储能动态分配空间，空间利用率高，链表存储的数据结构必须从链头开始，数据查找效率低

二叉查找树：数据插入和删除操作效率高，能动态分配空间，空间利用率高，数据查找效率高O(logn)

表达式树

表达式树是一种特殊类型的树，其叶结点是操作数（operand），包括常量和变量，而其它结点为操作符（operator）：

（1）由于操作符一般都是双目的，通常情况下该树是一棵二叉树；

（2）对于单目操作符（如++），其只有一个子结点。

表达式树一般由后缀表达式来生成。

堆

堆是一种特殊类型的二叉树，具有以下两个性质：

（1）每个结点的值大于（或小于）等于其每个子结点的值；

（2）该树完全平衡，其最后一层的叶子都处于最左侧的位置。

满足上面两个性质定义的是大顶堆（max heap）（或小顶堆min heap）。这意味着大顶堆的根结点包含了最大的元素，小顶堆的根结点包含了最小的元素。

由于堆是一棵完全平衡树，可以通过数组来存储并实现：

heap[i] ≧heap[2*i]

heap[i] ≧heap[2*i+1]

堆结构的最大好处是元素查找、插入和删除效率高

堆的主要应用：

（1）可用来实现优先队列（Priority Queue）

（2）用来实现一种高效排序算法-堆排序（Heap Sort），在排序一讲中详细介绍

大顶堆是一棵完全二叉树，二叉树中任何一个分支结点的值都大于或者等于它的孩子结点的值，并且每一棵子树也满足大顶堆的特性。

单节点二叉树为堆

在完全二叉树中所有以叶子结点(序号i > n/2)为根的子树是堆

堆中第一个非叶子结点的序号为n/2 - 1

堆

// h[N]存储堆中的值, h[1]是堆顶，x的左儿子是2x, 右儿子是2x + 1
// ph[k]存储第k个插入的点在堆中的位置
// hp[k]存储堆中下标是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

// 交换两个点，及其映射关系
void heap_swap(int a, int b)
{
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u)
{
    int t = u;
    if (u * 2 <= size && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        heap_swap(u, t);
        down(t);
    }
}

void up(int u)
{
    while (u / 2 && h[u] < h[u / 2])
    {
        heap_swap(u, u / 2);
        u >>= 1;
    }
}

// O(n)建堆
for (int i = n / 2; i; i -- ) down(i);

堆排序

#include<stdio.h>

#define N 100010

int n;
int h[N], cnt;

void down(int u)
{
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t)
    {
        int tmp = h[u];
        h[u] = h[t];
        h[t] = tmp;
        down(t);
    }
}

int main()
{
    int m;
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;
    
    for (int i = n / 2; i; i -- ) down(i);
    
    while(n -- )
    {
        printf("%d ", h[1]);
        h[1] = h[cnt -- ];
        down(1);
    }
    
    return 0;
}

二叉搜索树

效率O(logn)最差为O(n)退化二叉树的情况

#include<stdio.h>

#define N 10010

int n;
int w[N], l[N], r[N], idx;
int root;

void insert(int *u, int x)
{
    if (*u == 0)
    {
        *u = ++ idx ;
        w[*u] = x;
    }
    else if (x < w[*u]) insert(&l[*u], x);
    else if (x > w[*u]) insert(&r[*u], x);
}

void dfs(int u, int i)
{
    if (!u) return;
    if (i == 1) printf("%d ", w[u]);
    dfs(l[u], i);
    if (i == 2) printf("%d ", w[u]);
    dfs(r[u], i);
    if (i == 3) printf("%d ", w[u]);
}

int main()
{
    scanf("%d", &n);
    
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        insert(&root, x);
    }
    
    for (int i = 1; i <= 3; i ++ )
    {
        dfs(root, i);
        printf("\n");
    }
    
    return 0;
}

(139条消息) 数组模拟二叉搜索树（二叉排序树）_数组模拟二叉树_铁头娃撞碎南墙的博客-优快云博客

#include<stdio.h>

#define N 100010
#define INF 1e8
#define max(x, y) x > y ? x : y
#define min(x, y) x < y ? x : y

int l[N], r[N], w[N], idx;
int n;
int root;

void insert(int* u, int x)
{
    if (*u == 0)
    {
        *u = ++ idx;
        w[*u] = x;
    }
    else if (x < w[*u]) insert(&l[*u], x);
    else if (x > w[*u]) insert(&r[*u], x);
}

void del(int *u, int x)
{
    if (*u == 0) return;
    if (x < w[*u]) del(&l[*u], x);
    else if (x > w[*u]) del(&r[*u], x);
    else
    {
        if (!l[*u] && !r[*u]) *u = 0;//如果是叶子结点直接删除
        else if (!r[*u]) *u = l[*u];//如果右子树为空，左子树替换
        else if (!l[*u]) *u = r[*u];//如果左子树为空，右子树替换
        else
        {
            int p = l[*u];
            while (r[p]) p = r[p];
            w[*u] = w[p];//直接将值进行替换
            del(&l[*u], w[p]);//在左子树中删掉前驱
        }
    }
}

int get_pre(int u, int x)
{
    if (!u) return -INF;
    
    if (w[u] >= x) return get_pre(l[u], x);
    return max(w[u], get_pre(r[u], x));
}

int get_post(int u, int x)
{
    if (!u) return INF;
    
    if (w[u] <= x) return get_post(r[u], x);
    return min(w[u], get_post(l[u], x));
}

int main()
{
    scanf("%d", &n);
    
    while (n -- )
    {
        int t, x;
        scanf("%d%d", &t, &x);
        if (t == 1) insert(&root, x);
        else if (t == 2) del(&root, x);
        else if (t == 3) printf("%d\n", get_pre(root, x));
        else printf("%d\n", get_post(root, x));
    }
}