树和森林与二叉树

一、树的存储结构

 孩子兄弟表示法--CSNode

 二、树、森林与二叉树转换   都是用的孩子兄弟表示法

 

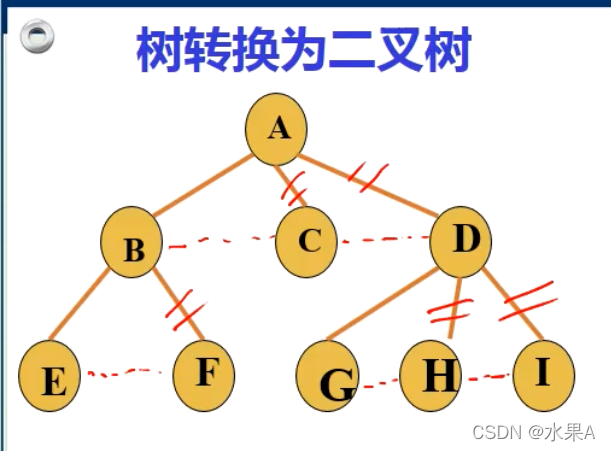
 树转换为二叉树后，根结点无右子树，因为树中的根结点没有兄弟。

例一：设树的结点个数为n,那么当把树T转换成一棵二叉树后，且根结点的左子树上有(n-1)个结点。

例二：设树的结点个数为n,那么当把树T转换成一棵二叉树后，且根结点的右子树上有(0)个结点。

例三：设T是一棵树，B是由T变换得的二叉树。若T中有n个非终端结点(度不为0的结点)，则B中右指针域为空的结点有（n+1）个。画个B、T看看。①转化后的二叉树根结点右指针域为空(树的根结点没有兄弟)；②树中每个非终端节点最后一个孩子无兄弟，转换为二叉树(右指针为兄弟)后，右指针为空。

 

左分支是孩子，右分支是兄弟 

由上图二叉树可知：B是A的孩子，C是B的兄弟，D是C的兄弟。所以B、C、D都是A的孩子。E、F是B的孩子。G、H、I是D的孩子

 森林里边有若干棵树，将每棵树转换为二叉树；将第二棵树的根结点看作是第一棵树根结点的兄弟，将第三棵树的根结点看作是第二棵树根结点的兄弟，即每棵树的根结点互为兄弟(所以在右分支画)

可知左子树就是第一棵树的子孙，右子树是第一棵树、第二棵树。

例一：设森林T中有4棵树，第一、二、三、四棵树的结点个数分别是n1,n2,n3,n4,那么当把森林T转换成一棵二叉树后，且根结点的右子树上有(n2+n3+n4)个结点。

例二：设F是一个森林，B是由F变换得的二叉树。若F中有n个非终端结点，则B中右指针域为空的结点有（n+1）个。①森林的每棵树的每个非终端节点最后一个孩子无兄弟，转换为二叉树(右指针为兄弟)后，右指针为空。②最后一棵树的根无兄弟

 三、树、森林遍历

要求：给定一棵树，写出先根遍历序列、后根遍历序列；给定森林，写出先序遍历序列、中序遍历序列；树与二叉树之间的相互转换；森林与二叉树之间的相互转换(画图题)

树采用孩子兄弟表示法，所以采用的存储结构是CSNode类型的

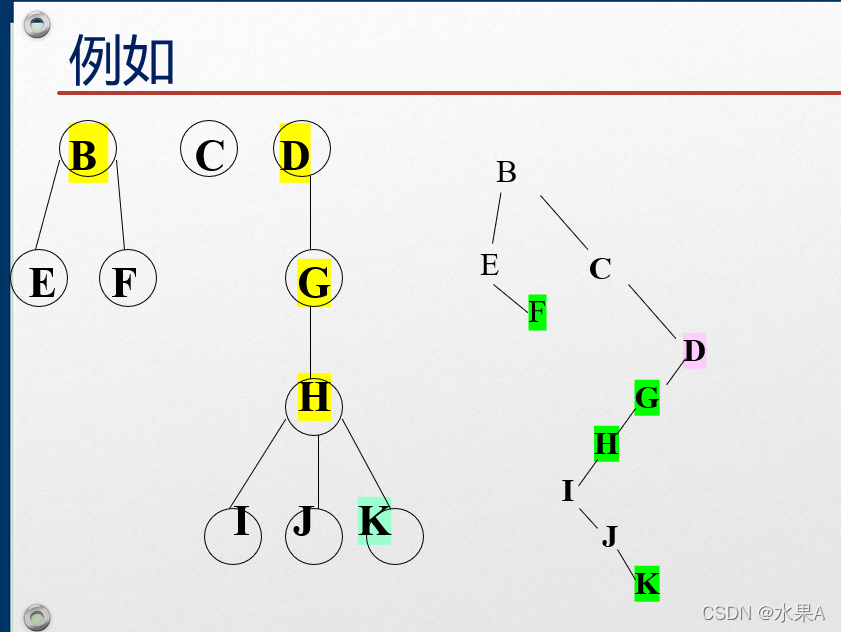
遍历这棵树用后根遍历时:E F B C I J K H G D A顺序与转换后的二叉树用中序遍历一致

树的先根遍历序列就是转换后的二叉树的先序遍历序列，树的后根遍历序列就是转换后的二叉树的中序遍历序列。

转换后的二叉树如下图：

 

例一： 如果T1是由有序树T转化而来的二叉树，那么T中结点的后根遍历就是T1中结点的(中序）。

 

 

 森林的先序遍历就是转换后的二叉树的先序遍历，森林的中序遍历序列(我怎么觉得看上去也像是森林的后序呢)就是转换后的二叉树的后序遍历。

---

 四、哈夫曼树

1.路径：由一个结点(一般为根结点)到另一个结点所经过的分支所构成。                                       2.路径长度：路径上的分支数目 

3.树的路径长度：每个结点的路径长度之和

a到a的路径长度为0，a到b的路径长度为1，a到d的路径长度为2.....

4.带权路径长度：结点到根的路径长度与结点上权的乘积

5.树的带权路径长度WPL：树中所有叶子结点的带权路径长度之和(假设有n个叶子结点。路径长度为I，权值为W)

 6.哈夫曼树：带权路径长度最小的二叉树

哈夫曼树：带权路径长度最小的二叉树

 因为哈夫曼树是带权路径长度最小的二叉树，所以让叶子结点越矮越好。由上图知，叶子结点是5个，又由二叉树的性质3：N0=N2+1。所以度为2的结点数为4。N1=0，无度为1的结点

故哈夫曼树中，总结点数一定是奇数个 

---

二、哈夫曼树(最优二叉树)构造的过程 

给定(5个叶子结点)A、B、C、D、E,构造一棵二叉树使WPL的值最小(树中所有叶子结点的带权路径长度之和)

 

实际上，构造过程是构造非终端结点的

 

 

 

 2.3两步要循环n-1次

 

 这种题得先自己构造完之后再算