回溯算法基本思想和常见题型-优快云博客

本文链接：https://blog.youkuaiyun.com/m0_62515800/article/details/129734105

回溯算法是什么,感兴趣可以看我上一篇文章:https://blog.youkuaiyun.com/m0_62515800/article/details/129732513

回溯算法的基本思想:

适用:求搜索问题和优化问题,且要满足多米诺性质

搜索空间:树,结点对应部分解向量,可行解在树叶上

搜索过程:采用系统的方法隐含遍历搜索树

搜索策略:深度优先,宽度优先,函数优先,宽深结合等

结点分支判定条件:满足约束条件--分支扩张解向量;不满足分支条件--回溯到该结点的父结点

存储:当前路径

回溯算法的常见类型:

子集类型

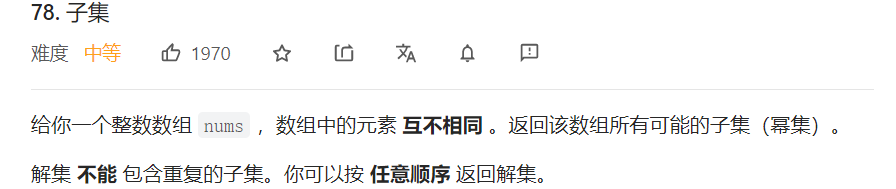
其实这类型题目有两个思路:用path[i]来存储路径

a.枚举第i步选择还是不选择这个字母加入路径

class Solution {       
      List<List<Integer>> re= new ArrayList<>();
      public List<List<Integer>> subsets(int[] nums) {
        List<Integer> one=new ArrayList<>();
        dfs(nums,0,one);
        return re;
    }
   private void dfs(int[] nums,int idx, List<Integer> one){
   if(idx==nums.length){    
       re.add(new ArrayList<>(one));
       return;
   }
  
       //nums[idx]不加入子集
        dfs(nums,idx+1,one);
       
       //nums[idx]加入子集
       one.add(nums[idx]);
       dfs(nums,idx+1,one);
       one.remove(one.size()-1);      
 }   
}

b.枚举所以情况:加入path

class Solution {  
     List<List<Integer>> re= new ArrayList<>();
      public List<List<Integer>> subsets(int[] nums) {
        List<Integer> one=new ArrayList<>();
        dfs(nums,0,one);
        return re;
    }
   private void dfs(int[] nums,int idx, List<Integer> one){
       re.add(new ArrayList<>(one));
       if(idx==nums.length) return;
       for(int j=idx;j<nums.length;j++){//
           one.add(nums[j]);
           dfs(nums,j+1,one);
           one.remove(one.size()-1);
       }
}

组合类型

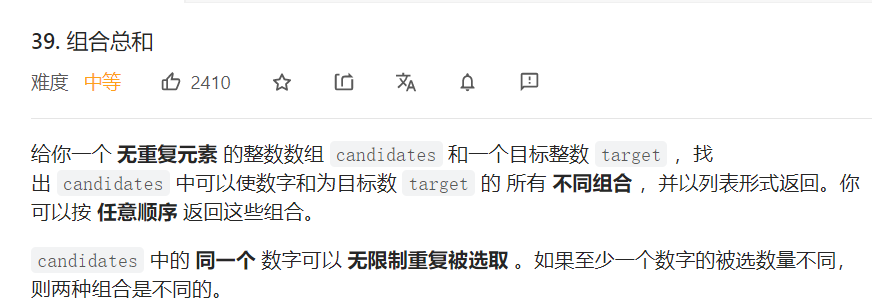
class Solution {
    private final List<Integer> path = new ArrayList<>();
    private final List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        this.k=candidates.length;
        dfs(0,target,candidates);
        return ans;
    }
    public void dfs(int idx,int target,int[] candidates){
        //剪枝,数组不排序的话
        //if( target<0) return;
        if(target==0){
            ans.add(new ArrayList<>(path));
            return;
        }
        //枚举所以情况
        for(int j=idx;j<candidates.length;j++){
             // 剪枝(数组已升序排序),减掉减去这个结点为根的树
            if (target - candidates[j] < 0) {
                break;
            }
            path.add(candidates[j]);
            dfs(j,target-candidates[j],candidates);
            path.remove(path.size()-1);
        }


    }
}

排列类型

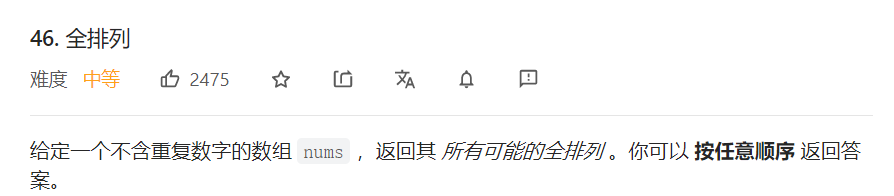
class Solution {
    List<List<Integer>> re= new ArrayList<>();
    public List<List<Integer>> permute(int[] nums) {
        int[] visited = new int[nums.length];
        List<Integer> one=new ArrayList<>();
        dfs(nums,visited,one);
        return re;
    }
    private void dfs(int[] nums,int[] visited, List<Integer> one){
        if(one.size()==nums.length){
            re.add(new ArrayList<>(one));
            return;
        }
        //枚举所有情况
        for(int i=0;i<nums.length;i++){
            //不同层循环不能两次选择自己,
            //visited[i]=1表示上一层已经用过索引为i的数,不能再选择
            if(visited[i]==1) continue;
            visited[i]=1;
            one.add(nums[i]);
            dfs(nums,visited,one);
            visited[i]=0;
            one.remove(one.size()-1);
        }
    }
}

变形,灵活改变类型

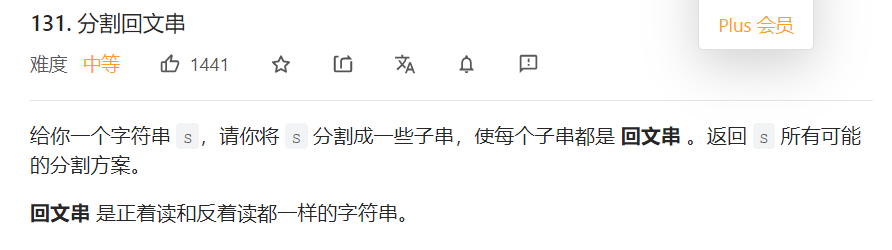
向这类题,没有说是子集型,我们可以灵活处理,比如说看成是子集型

把aab看成是a,a,b 这样我们就把问题转换成","选择还是不选择的问题了

就对应子集型的a情况,下面是代码实现

class Solution {
    private final List<List<String>> ans = new ArrayList<>();
    private final List<String> path = new ArrayList<>();
    private String s;

    public List<List<String>> partition(String s) {
        this.s = s;
        dfs(0,0);
        return ans;
    }

    private boolean ishuiwen(int l,int r){
        while(l<r){
            if(s.charAt(l++)!=s.charAt(r--)) return false;           
        }
        return true;
    }

    public void dfs(int idx,int start){// start 表示当前这段回文子串的开始位置
        if(idx==s.length()){
            ans.add(new ArrayList<>(path));
            return;
        }
             // 不选 i 和 i+1 之间的逗号（注意i=n-1 时右边没有逗号）
             if(idx<s.length()-1)
            dfs(idx+1,start);
             // 选 i 和 i+1 之间的逗号
            if(ishuiwen(start,idx)){
                path.add(s.substring(start,idx+1));
                dfs(idx+1,idx+1);
                path.remove(path.size()-1);//恢复现场
            }
        }
    

}

当然,这道题我们也可以用枚举所以情况的方法来解,大家可以自己试一下再来看答案哦!

class Solution {
    private final List<List<String>> ans = new ArrayList<>();
    private final List<String> path = new ArrayList<>();
    private String s;
    public List<List<String>> partition(String s) {
        this.s = s;
        dfs(0,0);
        return ans;
    }

    private boolean ishuiwen(int l,int r){
        while(l<r){
            if(s.charAt(l++)!=s.charAt(r--)) return false;           
        }
        return true;
    }   

   public void dfs(int idx){
       if(idx==s.length()){
           ans.add(new ArrayList<>(path));
           return;
       }
       for(int j=idx;j<s.length();j++){//枚举子串位置
           if(ishuiwen(idx,j)){
               path.add(s.substring(idx,j+1));
               dfs(j+1);
               path.remove(path.size()-1);//恢复现场
          }
       }
   }

}