目录
6. 后序遍历 (Post-Order Traversal)
1. 前言
!FBI WARNING!
本文旨在于以通俗易懂地方式阐述二叉树遍历方法
什么是二叉树?

二叉树(Binary Tree)是每个节点最多只有两个分支的树结构,通常分支被称作“左子树”或“右子树”,不能随意颠倒。
2. 二叉树存储结构
二叉树可以用数组或链接串列来存储,若是满二叉树就能紧凑排列而不浪费空间。
一图解百惑,上图!

二叉树通常用树结点结构来存储。使用链表能避免顺序存储浪费空间的问题,算法和结构相对简单。
一图解百惑,上图!
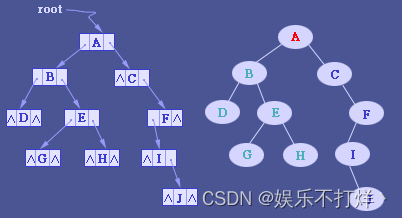
3. 遍历命名方式
遍历命名方式,源于其访问节点的顺序。最简单的划分:是深度优先(先访问子节点,再访问父节点,最后是第二个子节点)?还是广度优先(先访问第一个子节点,再访问第二个子节点,最后访问父节点)?
广度优先搜索算法(Breadth-First Search,BFS)是一种暴力搜索算法,从根节点开始,沿着树的宽度遍历树的节点,如果所有节点均被访问,则算法中止。
深度优先搜索算法(Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。当节点的所在边都己被探寻过,搜索将回溯到发现节点的那条边的起始节点,这一过程一直进行到已发现从源节点可达的所有节点为止。
一图解百惑,上图!
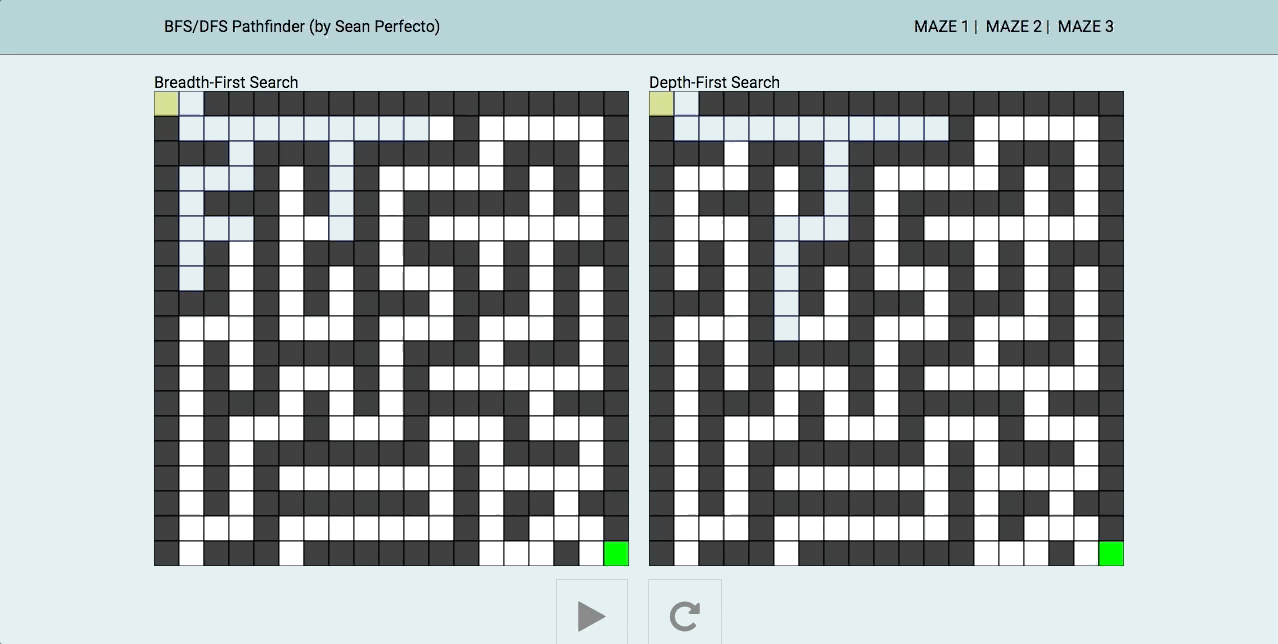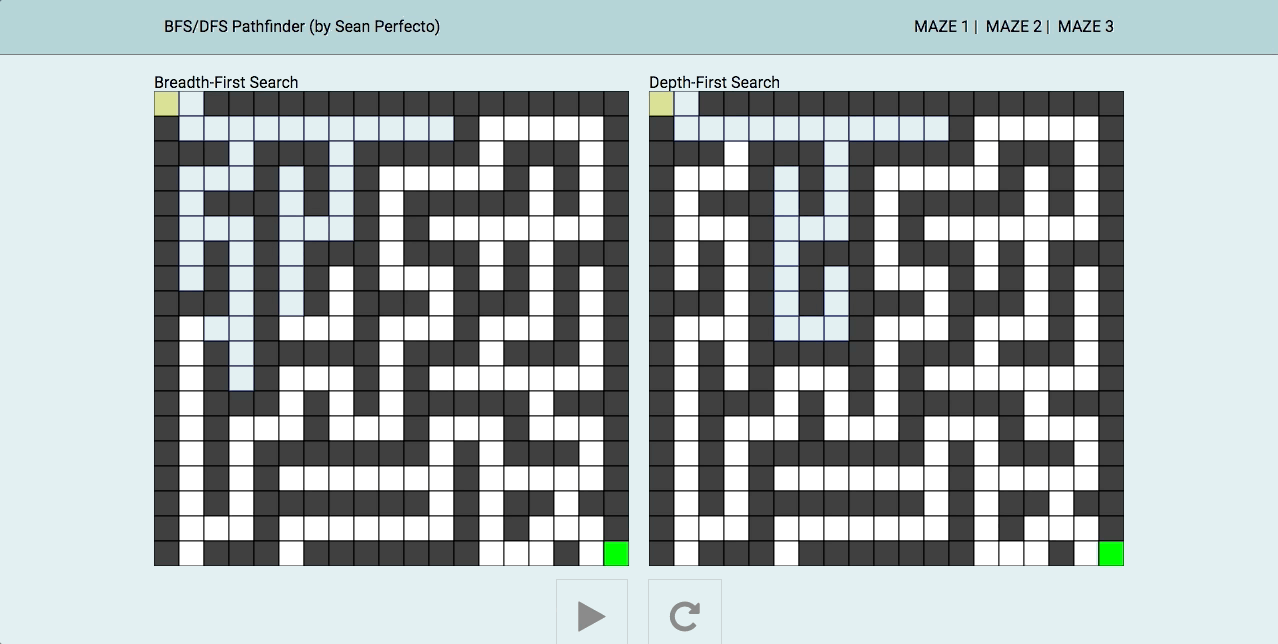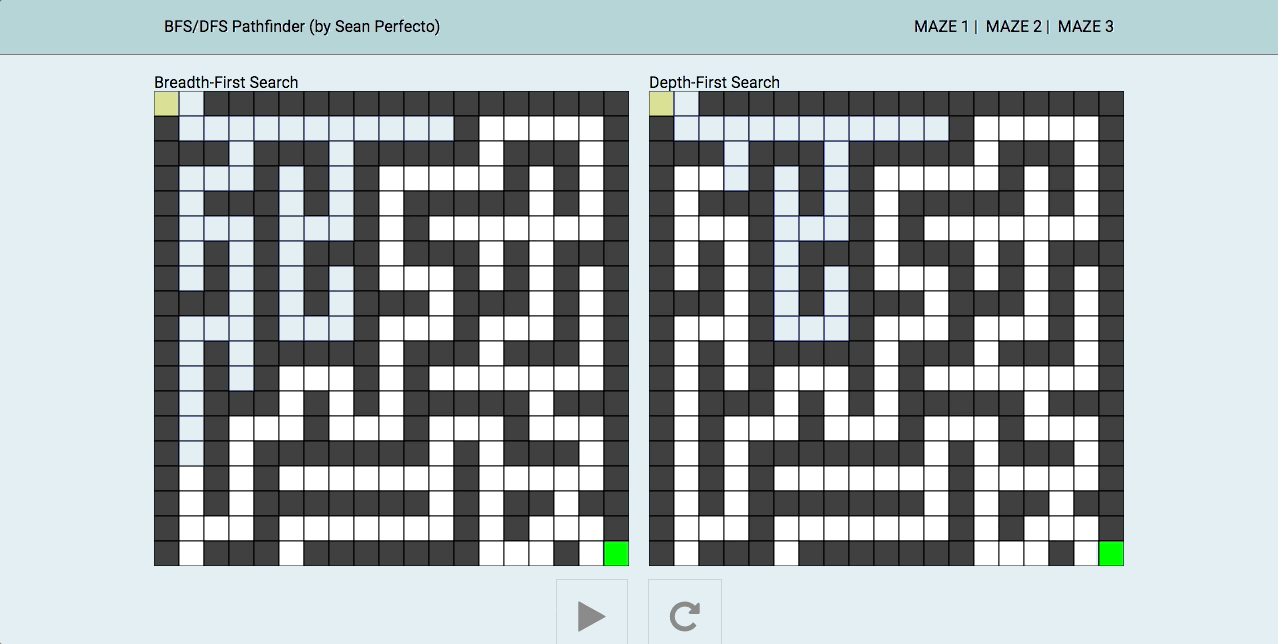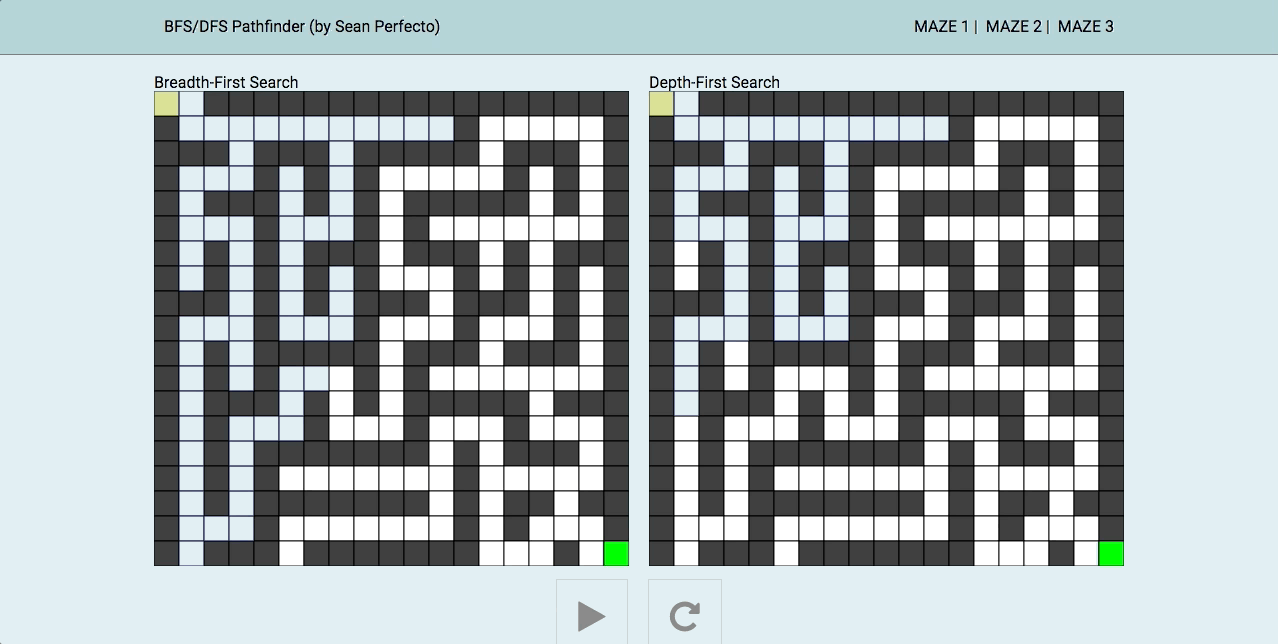
深度优先可进一步按照根节点相对于左右子节点的访问先后来划分。对广度优先而言,遍历没有前序中序后序之分:给定一组已排序的子节点,其“广度优先”的遍历只有一种唯一的结果。
4. 前序遍历 (Pre-Order Traversal)
如果把左节点和右节点的位置固定不动,那么根节点放在左节点的左边,称为前序(Pre-order)。
一图解百惑,上图!

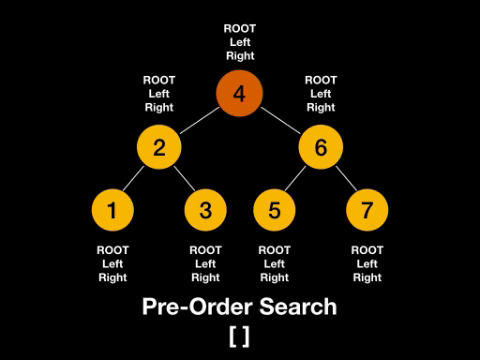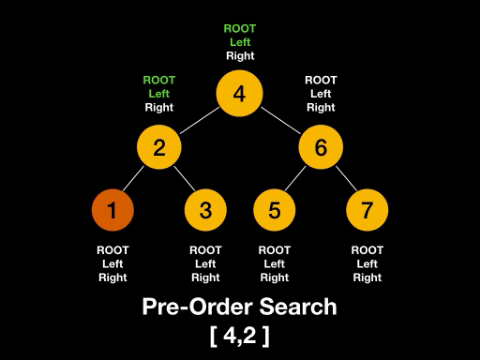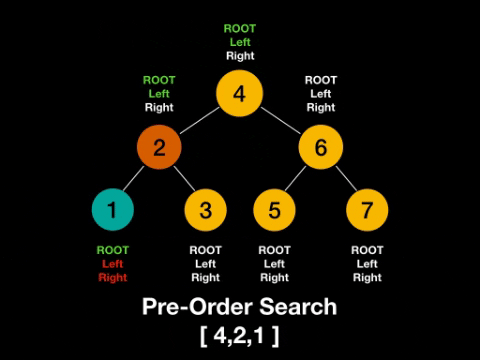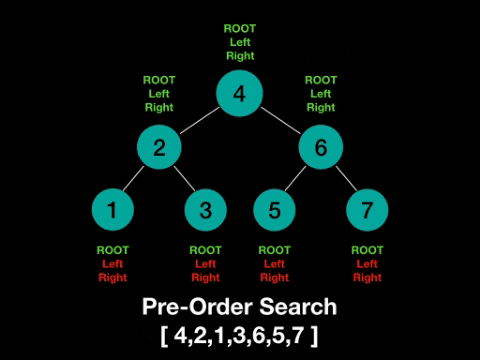
话不多说,上代码!二叉树的前序遍历(Python)
5. 中序遍历 (In-Order Traversal)
根节点放在左节点和右节点的中间,称为中序(In-order)。
一图解百惑,上图!

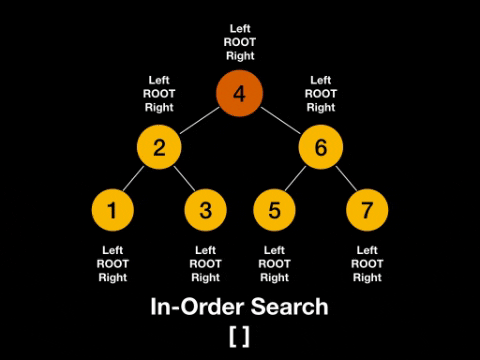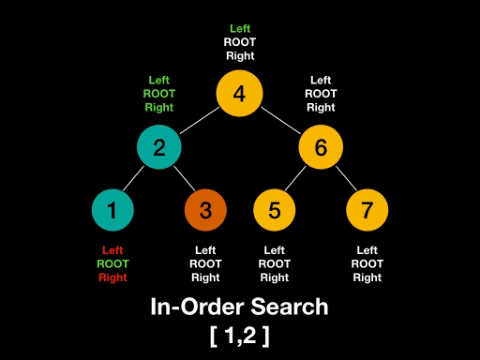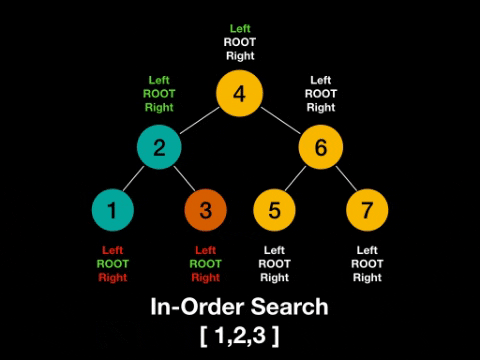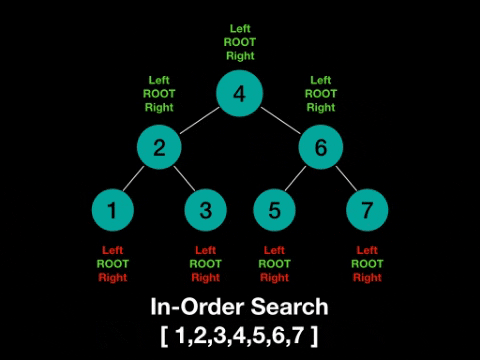
话不多说,上代码!二叉树的中序遍历(Python)
6. 后序遍历 (Post-Order Traversal)
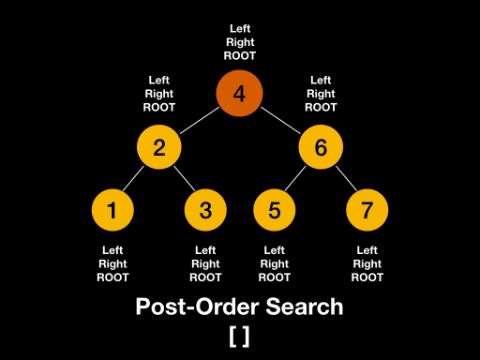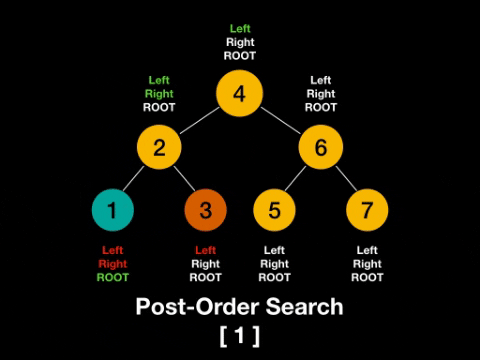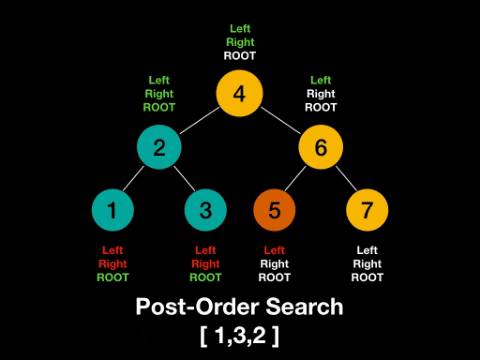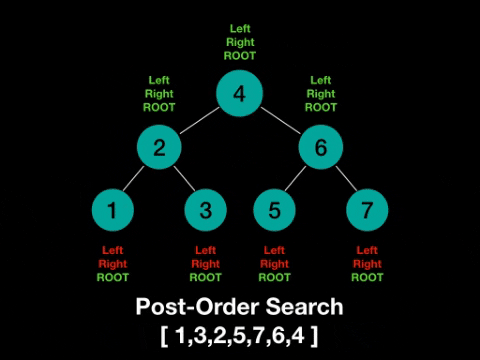
根节点放在右节点的右边,称为后序(Post-order)。
一图解百惑,上图!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








