A st
A star
优先队列BFS
优先队列BFS:该算法维护一个优先队列(二叉堆),不断从堆中取出“当前代价最小”的状态
(堆顶)进行扩展。每个状态第一次从堆中取出时,就得到了从初始状态到该状态的最小代价。
问题:如果给定一个“目标状态”,需要求出从初态到目标状态的最小代价,那么优先队列BFS
的这个“优先策略”显然是不完善的。一个状态的当前代价最小,只能说明从初始状态到该状态
的代价很小,而在未来的搜索中,从该状态到目标状态可能会花费很大的代价。另外一些状态
虽然当前代价略大,但是未来到目标状态的代价可能会很小,于是从起始状态到目标状态的总
代价反而更优。优先队列BFS会优先选择前者的分支,导致求出最优解的搜索量增大。
估价函数
如果能够对未来可能产生的代价进行预估,就可以提高搜索效率。确切的说,设计一个“估价函数”,以任意“状态”为输入,计算从该状态到目标状态所需代价的估计值。在搜索中仍然维护一个优先队列(二叉堆),不断从堆中取出“当前代价 + 估计值”最小的状态进行扩展。
为了保证第一次从堆中取出目标状态时得到的就是最优解,我们设计的估价函数需要满足一个
基本准则:
设当前状态now到目标状态dst所需代价的估计值为:f(now)。
设在未来搜索中,实际求出的从当前状态now到目标状态dst的最小代价为g(now)。
对于任意的状态now,应该有f(now) <= g(now)。
也就是说,估价函数的估值不能大于未来实际代价,估价要比实际代价更优。
为什么f(now)必须<= g(now)?
根据每次取出“当前代价 + 估计值”最小的状态进行扩展的策略,会得到如下过程。
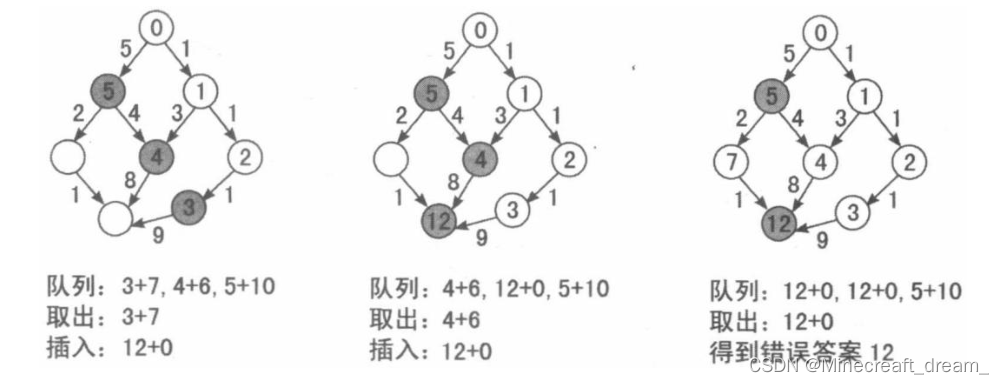
本来在最优解搜索路径上的状态被错误的估计了较大的代价,被压在堆中无法取出,从而导致
非最优解搜索路径上的状态不断扩展,直至在目标状态上产生错误的答案。
如果我们在设计估价函数时确保f(now) <= g(now)(保证估值不大于未来实际代价),那么即使估值不太准确,导致非最优搜索路径上的状态stat先被扩展,但是随着“当前代价”的不断累加,在目标状态被取出之前的某个时刻必然会出现以下两种情况之一:
结合以上两点,可知 d(y) + f(y) < d(x) + f(x),因此y就会被从堆中取出进行扩展,最终更新到目标状态上,产生最优解。
① 对于非最优路径上的状态x,设x的当前代价为d(x),并且d(x) + f(x) > 起始状态到目标状态的最小代价。
② 对于最优解路径上的状态y,因为f(y) <= g(y),设y的当前代价为d(y),则:d(y) + f(y)<= d(y) + g(y),而后者的含义就是从初试状态到目标状态的最小代价。
结合以上两点,可知 d(y) + f(y) < d(x) + f(x),因此y就会被从堆中取出进行扩展,最终更新到目标状态上,产生最优解。
这种带估价函数的优先队列BFS就称为A算法。只要保证对于任意状态stat,都有f(stat) <=
g(stat),A算法就一定能在目标状态第一次从堆中被取出时得到最优解。并且在搜索过程中,
每个状态只需要被扩展一次(之后再被取出就可以直接忽略)。估价函数f(stat)越准确,越接
近g(stat),A算法的效率就越高。如果估值始终为0(任意f(stat) = 0),就等价于普通的优
先队列BFS。
A算法提高搜索效率的关键,就在于能否设计出一个优秀的估价函数。估价函数在满足上
述设计准则的前提下,还应该尽可能反应未来实际代价的变化趋势和相对大小关系,这样
搜索才会较快地逼近最优解。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










