栈（C语言实现）

目录

一、栈的基本概念

1.栈的定义

2.栈的基本操作

二、栈的顺序存储结构

         1.顺序栈定义

2.顺序栈实现（top指针指向栈顶元素下一个位置）

3.共享栈（知识漏洞）

三、栈的链式存储结构

1.链式栈定义

         2.链式栈实现

四、栈的应用

1.括号匹配

2.栈在表达式求值中的应用

3.栈实现队列

---

一、栈的基本概念

1.栈的定义

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。 进行数据插入和删除操作的一端 称为栈顶，另一端称为栈底。 栈中的数据元素遵守后进先出 LIFO （ Last In First Out ）的原则。

注：栈的数学性质

n个不同的元素进栈，出栈元素不同排列的个数为：

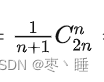
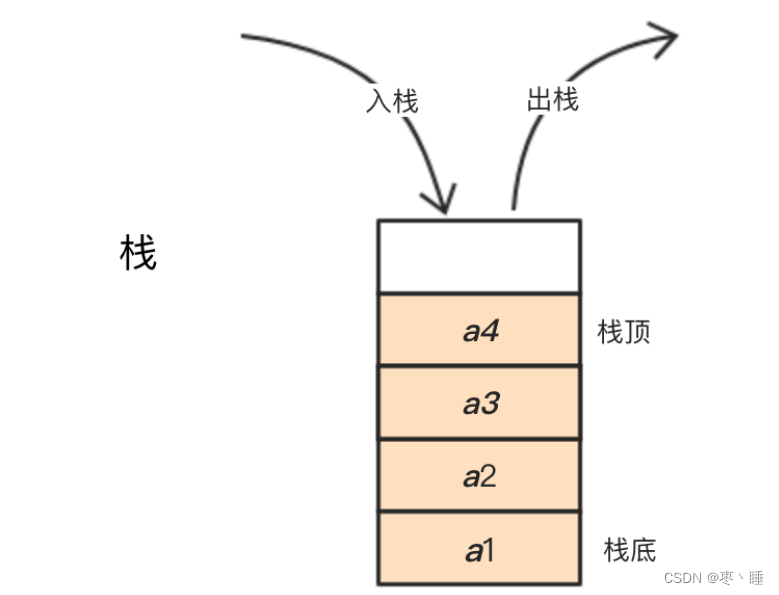
2.栈的基本操作

// 初始化栈 
void StackInit(Stack* ps);
// 入栈 
void StackPush(Stack* ps, STDataType data);
// 出栈 
void StackPop(Stack* ps);
// 获取栈顶元素 
STDataType StackTop(Stack* ps);
// 获取栈中有效元素个数 
int StackSize(Stack* ps);
// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
bool StackEmpty(Stack* ps);
// 销毁栈 
void StackDestroy(Stack* ps);

二、栈的顺序存储结构

1.顺序栈定义

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top），指示当前栈顶元素的位置（或当前栈顶元素的下一个位置）。

栈的顺序存储类型可描述为：

typedef int STDataType;
typedef struct Stack
{
	STDataType* pst;
	int top;
	int capacity;
}Stack;

2.顺序栈实现（top指针指向栈顶元素下一个位置）

注：当top指针指向栈顶元素下一个位置时，栈为空，top指针初始化为0

        若top指针指向栈顶元素，则栈为空时，top初始化为-1

// 初始化栈 
void StackInit(Stack* ps)
{
	ps->pst = NULL;
	ps->top = 0;//指向栈顶元素后面
	ps->capacity = 0;
}
// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);

	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->pst, newCapacity*sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		ps->pst = tmp;
		ps->capacity = newCapacity;
	}
	ps->pst[ps->top] = data;
	ps->top++;
}
// 出栈 
void StackPop(Stack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));//确保栈不为空
	ps->top--;
}
// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(ps);
	int top = ps->top;
	return (ps->pst)[top-1];
}
// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->top;
}
// 检测栈是否为空
bool StackEmpty(Stack* ps)
{
	assert(ps);
	if (ps->top == 0)
	{
		return true;
	}
	return false;
}
// 销毁栈 
void StackDestroy(Stack* ps)
{
	assert(ps);
	free(ps->pst);
}

 3.共享栈（知识漏洞）

利用栈底位置相对不变的特性，可让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延申。

、

（1）两个栈的栈顶指针都指向栈顶元素，top0=-1时，蓝色栈为空；top1=MaxSize时，绿色栈为空；

（2）仅当两个栈栈顶指针相邻（top1-top0==1）时，判断栈满。

（3）当蓝色栈进栈时，top0先+1，再赋值，绿色栈进栈时top1先-1，再赋值；出栈时相反

（目的是先判断有没有空间再确定是否赋值，防止覆盖掉或删掉原有数据）

优点：共享栈是为了更有效的利用储存空间，两个栈的空间相互调节，只有在整个储存空间被占满

时才发生上溢，其存取数据的时间复杂度均为O（1），所以对存取效率没有影响。

三、栈的链式存储结构

1.链式栈定义

采用链式存储的栈称为链栈。、

优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。

typedef int DataType;

typedef struct StackNode
{
	DataType date;
	struct StackNode* next;
}SNode;

typedef struct ListStack
{
	int capacity;
	SNode* top;
}LStack;

2.链式栈实现

注：通常采用单链表实现，并规定所有操作都在单链表表头进行，这里规定链栈没有头结点

SNode* BuyNode(DataType x)
{
	SNode* node = (SNode*)malloc(sizeof(SNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->date = x;
	node->next = NULL;

	return node;
}

// 初始化栈 
void StackInit(LStack* ps)
{
	ps->capacity = 0;
	ps->top = NULL;
}
// 入栈 
void StackPush(LStack* ps, DataType data)
{
	assert(ps);
	SNode* node = BuyNode(data);
	//栈为空
	if (StackEmpty(ps))
	{
		ps->top = node;
		ps->capacity++;
	}
	//栈不为空
	//此时top指向头结点，此时插入就是单链表头插
	else
	{
		node->next = ps->top;
		ps->top = node;
		ps->capacity++;
	}
}
// 出栈 
void StackPop(LStack* ps)
{
	assert(ps);
	assert(!StackEmpty(ps));
	//单链表头删
	SNode* tmp = ps->top;
	ps->top = ps->top->next;
	free(tmp);
	ps->capacity--;
}
// 获取栈顶元素 
DataType StackTop(LStack* ps)
{
	assert(!StackEmpty(ps));
	return ps->top->date;
}
// 获取栈中有效元素个数 
int StackSize(LStack* ps)
{
	return ps->capacity;
}
// 检测栈是否为空
bool StackEmpty(LStack* ps)
{
	return ps->top == NULL;
}
// 销毁栈 
void StackDestroy(LStack* ps)
{
	assert(ps);
	while (!StackEmpty(ps))
	{
		StackPop(ps);
	}
	ps->top = NULL;
}

四、栈的应用

1.括号匹配

思路：

第一步：依次遍历字符串，如果是左部分括号，依次入栈，

               如果遇到右部分括号，若栈为空，则无效括号，若与栈顶元素匹配，则栈顶元素出栈

第二步：遍历完字符串后判断栈是否为空，如果栈为空，则括号一一匹配，有效，否则无效

第三步：释放内存

LStack st;
bool isValid(char * s){
    StackInit(&st);
    while(*s)
    {
        if(*s=='('
        || *s=='['
        || *s=='{')
        {
            StackPush(&st,*s);
        }
        else
        {
            if(StackEmpty(&st))
            {
                StackDestroy(&st);
                return false;
            }
            char c=StackTop(&st);
            //printf("%c",c);
            if(c=='(')
            {
                if(*s!=')')
                {
                    StackDestroy(&st);
                    return false;
                }
            }
            else if(c=='[')
            {
                if(*s!=']')
                {
                    StackDestroy(&st);
                    return false;
                }
            }
            else if(c=='{')
            {
                if(*s!='}')
                {
                    StackDestroy(&st);
                    return false;
                }
            }
            StackPop(&st);
        }
        s++;
    }
    if(!StackEmpty(&st))return false;
    StackDestroy(&st);
    return true;
}

2.栈在表达式求值中的应用

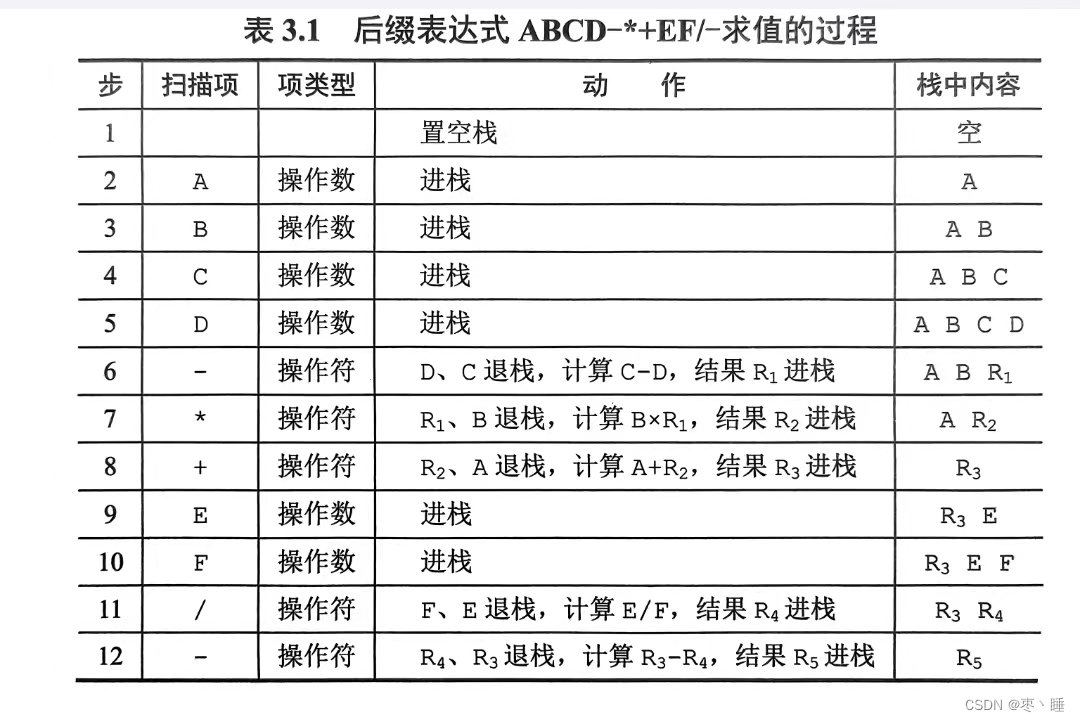
注：后缀表达式先出栈的是右操作数

        前缀表达式先出栈的是左操作数

中缀表达式转化为后缀表达式思路（知识漏洞）：

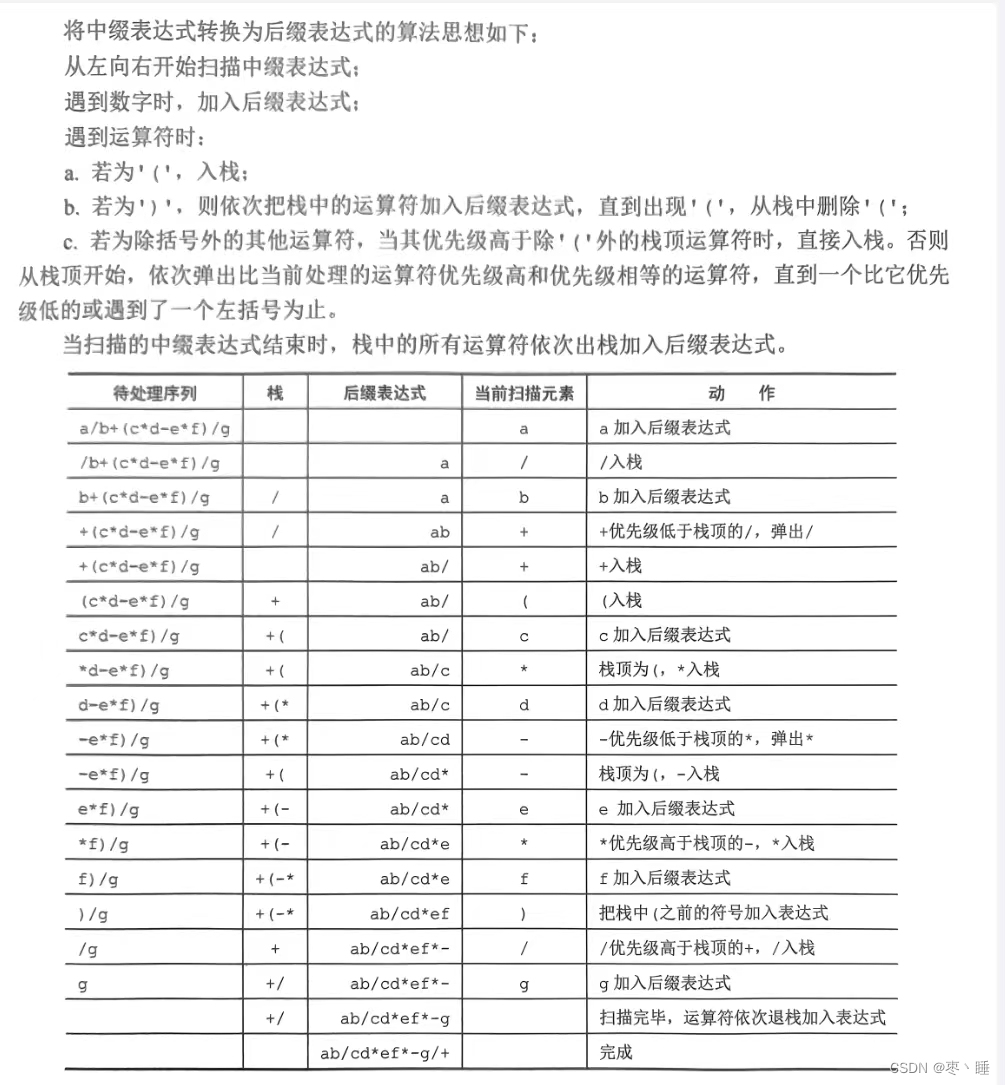
3.栈实现队列

思路：由于一组序列入栈再出栈会使序列倒序输出，而队列先进先出，则不会改变序列

所以利用一个栈作为inStack输入数据，输出的数据先进入outStack，再由outStack输出。

typedef struct {
    Stack stIn;
    Stack stOut;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* que=(MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&que->stIn);
    StackInit(&que->stOut);
    return que;
}

void myQueuePush(MyQueue* que, int x) {
    StackPush(&que->stIn,x);
}

int myQueuePop(MyQueue* que) {
    if(StackEmpty(&que->stOut))
    {
        while(!StackEmpty(&que->stIn))
        {
            StackPush(&que->stOut,StackTop(&que->stIn));
            StackPop(&que->stIn);
        }
    }
    if(StackEmpty(&que->stOut))
    {
        return -1;
    }
    int x=StackTop(&que->stOut);
    StackPop(&que->stOut);
    return x;
}

int myQueuePeek(MyQueue* que) {
    int x=myQueuePop(que);
    StackPush(&que->stOut,x);
    return x;
}

bool myQueueEmpty(MyQueue* que) {
    if(StackEmpty(&que->stIn)&&StackEmpty(&que->stOut))
    {
        return true;
    }
    return false;
}

void myQueueFree(MyQueue* que) {
    StackDestroy(&que->stOut);
    StackDestroy(&que->stIn);
    free(que);
}