线性表（顺序表和链表）

目录

（一）线性表的基本概念

1.基本概念

2.顺序表链表优缺点分析

（1）顺序表

（2）链表

（二）线性表的实现

1.顺序存储

2.链式存储

（1）无头非循环单向链表实现

（2）带头循环双向链表实现

（三）线性表应用（常见OJ题目）

数组相关OJ

1. 原地移除数组中所有的元素val，要求时间复杂度为O(N)，空间复杂度为O(1)。

2.合并两个有序数组。

链表相关OJ

1.反转链表

2.给定一个带有头结点 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则 返回第二个中间结点。

3.将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。

4.编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前 。

5.链表的回文结构。

6.输入两个链表，找出它们的第一个公共结点。

7.给定一个链表，返回链表开始入环的第一个结点。 如果链表无环，则返回 NULL

8.给定一个链表，每个结点包含一个额外增加的随机指针，该指针可以指向链表中的任何结点或空结点。 要求返回这个链表的深度拷贝。

---

（一）线性表的基本概念

1.基本概念

线性表 （ linear list ） 是 n 个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使

用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串 ...

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，

线性表在物理上存储时，通常以数组和链式结构的形式存储

2.顺序表链表优缺点分析

（1）顺序表

优点：

1. 随机访问：由于顺序表中的元素在内存中是连续存储的，因此可以通过下标直接访问元素，具有快速的随机存取能力。
2. 索引操作高效：插入和删除元素时，如果知道元素的位置，可以通过移动少量元素来完成，因此在索引操作上具有较高的效率。
3. 缓存友好：顺序表的元素存储在一段连续的内存中，更容易进行预读，有利于缓存的使用效率。

缺点：

1. 插入和删除元素的代价高：在顺序表中插入和删除元素，特别是在中间位置，需要移动大量元素，导致操作的代价较高。
2. 长度固定：顺序表的长度是固定的，当需要存储的元素个数超过长度限制时，需要重新分配内存空间，可能引发额外的开销。
3. 空间利用不灵活：顺序表的内存空间需要一次分配完毕，因此存在可能浪费的情况，特别是在存储的元素数量较少时。

（2）链表

优点：

1. 动态性：链表的长度可以动态增加或减少，不需要预先分配固定大小的内存空间，相比顺序表更加灵活。
2. 插入和删除操作高效：链表在插入和删除元素时，只需要修改节点之间的链接关系，不需要移动大量元素，因此在插入和删除操作上具有较高的效率。
3. 空间利用灵活：链表节点的内存可以分散在各个不同的位置，不存在连续内存空间的要求，因此可以充分利用零散的内存空间。

缺点：

1. 随机访问低效：链表中的元素并不是连续存储的，因此无法通过下标直接访问元素，需要从头遍历链表找到目标节点，导致随机访问的效率较低。
2. 额外空间占用：链表节点内除了存储数据外，还需要存储指向下一个节点的指针，因此相对于仅存储数据的顺序表，链表需要更多的存储空间。
3. 内存分配开销：链表节点是动态分配的，每次插入一个新节点都需要执行内存分配操作，可能会增加额外的开销。

（二）线性表的实现

1.顺序存储

顺序表是用一段 物理地址连续 的存储单元依次存储数据元素的线性结构，一般情况下采用数组存

储。在数组上完成数据的增删查改。

动态顺序表实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include"SeqList.h"

//初始化顺序表
void InitSeqList(SL* psl)
{
	assert(psl);
	psl->arr = (dataType*)malloc(sizeof(dataType)*4);
	if (psl->arr == NULL)
	{
		perror("InitMalloc");
		return;
	}
	psl->capacity = 4;
	psl->size = 0;
	printf("Init Success\n");
}
//检查容量
void CheckCapacity(SL* psl)
{
	assert(psl);
	if (psl->capacity == psl->size)
	{
		dataType* tmp = (dataType*)realloc(psl->arr, psl->capacity * sizeof(dataType)*2);
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		psl->arr = tmp;
		psl->capacity *= 2;
	}
}
//头插
void PushFrontSL(SL* psl,dataType x)
{
	//CheckCapacity(psl);
	//int i = 0;
	//for (i = psl->size - 1; i >= 0; i--)
	//{
	//	psl->arr[i + 1] = psl->arr[i];
	//}
	//psl->arr[0] = x;
	//psl->size++;
	InsertSL(psl, x, 0);
}
//尾插
void PushBackSL(SL* psl, dataType x)
{
	//CheckCapacity(psl);
	//psl->arr[psl->size] = x;
	//psl->size++;
	InsertSL(psl, x, psl->size);
}
//头删
void PopFrontSL(SL* psl)
{
	//assert(psl);
	//assert(psl->size > 0);
	//int i = 1;
	//for (i = 1; i < psl->size; i++)
	//{
	//	psl->arr[i - 1] = psl->arr[i];
	//}
	//psl->size--;
	EraseSL(psl, 0);
}
//尾删
void PopBackSL(SL* psl)
{
	//assert(psl);
	//assert(psl->size>0);
	//psl->size--;
	EraseSL(psl, psl->size - 1);
}
//插入到指定位置
void InsertSL(SL* psl, dataType x, int pos)
{
	CheckCapacity(psl);
	assert(pos <= psl->size && pos >= 0);
	int i = 0;
	for (i = psl->size - 1; i >= pos; i--)
	{
		psl->arr[i + 1] = psl->arr[i];
	}
	psl->arr[pos] = x;
	psl->size++;
}
//删除指定位置元素
void EraseSL(SL* psl, int pos)
{
	assert(psl);
	assert(pos >= 0 && pos < psl->size);
	int i = 0;
	for (i = pos + 1; i < psl->size; i++)
	{
		psl->arr[i - 1] = psl->arr[i];
	}
	psl->size--;
}
//修改数据
void ModifySL(SL* psl, int pos, dataType x)
{
	assert(psl);
	assert(pos >= 0 && pos < psl->size);
	psl->arr[pos] = x;
}
//查找数据
int FindSL(SL* psl, dataType x)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		if (psl->arr[i] == x)
		{
			return i;
		}
	}
	return -1;
}
//释放顺序表空间
void DestorySeqList(SL* psl)
{
	assert(psl);
	free(psl->arr);
	psl->arr = NULL;
	psl->capacity = 0;
	psl->size = 0;
}
//打印顺序表
void PrintSeqList(SL* psl)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		printf("%d ", psl->arr[i]);
	}
	printf("\n");
}

2.链式存储

（1）无头非循环单向链表实现

注意事项：

1.当对链表的操作需要修改头节点时，应当传参传头节点的二级指针，因为改变结构体需要传结构体指针，要改变头节点指针，则要传头节点指针的指针，也就是二级指针

2.头节点二级指针不会为空，当链表为空时，头节点二级指针也不会为空，因为他存的是头节点指针的地址，而不是头节点指针

3.删除时应当确保链表不为空

4.对链表进行插入删除操作时，由于本链表不含哨兵位头节点，所以应当分情况讨论 链表为空，链表只有一个节点，以及链表有多个节点，三种情况。

#define _CRT_SECURE_NO_WARNINGS 1
#include"SList.h"
//创建新节点
SLNode* BuyNode(DataTypeSL x)
{
	SLNode* newnode = (SLNode*)malloc(sizeof(SLNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}

//打印
void PrintSL(SLNode* phead)
{
	SLNode* cur = phead;
	while (cur)
	{
		printf("%d->", cur->data);
		cur = cur->next;
	}
	printf("NULL\n");
}

//头插
void PushFrontSL(SLNode** pphead, DataTypeSL x)
{
	assert(pphead);
	SLNode* newNode = BuyNode(x);//创建新节点
	newNode->next = *pphead;//让新节点的下个节点连上当前头节点
	*pphead = newNode;//将插入的这个新节点地址赋值给头节点从而作为新的头节点

}

//尾插
void PushBackSL(SLNode** pphead, DataTypeSL x)
{
	assert(pphead);
	SLNode* newNode = BuyNode(x);
	//没有节点
	if (*pphead == NULL)
	{
		*pphead = newNode;
		return;
	}
	//一个节点
	//多个节点
	SLNode* tail = *pphead;//创建一个头节点的临时拷贝，保证操作时头节点不改变
	while (tail->next != NULL)//找到尾节点
	{
		tail = tail->next;
	}
	tail->next = newNode;
}

//头删
void PopFrontSL(SLNode** pphead)
{
	assert(pphead);
	//如果链表本身为空，那再删除就报错
	assert(*pphead);
	//如果就一个数据
	//如果有多个节点
	SLNode* cur = *pphead;
	*pphead = (*pphead)->next;
	free(cur);
	cur = NULL;
}

//尾删
void PopBackSL(SLNode** pphead)
{
	assert(pphead);
	//如果链表本身为空，那再删除就报错
	assert(*pphead);
	SLNode* tail = *pphead;
	//只有一个数据
	//有多个数据
	while (tail->next!=NULL && tail->next->next != NULL)
	{
		tail = tail->next;
	}
	if (tail->next == NULL)
	{
		free(tail);
		*pphead = NULL;
	}
	else
	{
		free(tail->next);
		tail->next = NULL;
	}
}
//查找
SLNode* FindSL(SLNode* phead, DataTypeSL x)
{
	SLNode* cur = phead;
	while (cur)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	return NULL;
}
//目标节点后插入
void InsertBack(SLNode* pos, DataTypeSL x)
{
	assert(pos);
	SLNode* newNode = BuyNode(x);
	newNode->next = pos->next;
	pos->next = newNode;
}
//目标节点后删除
void EraseBack(SLNode* pos)
{
	assert(pos);
	assert(pos->next);
	SLNode* tmp = pos->next;//先保存要删除节点的位置，以便可以释放空间
	pos->next = pos->next->next;
	free(tmp);
}
//目标节点前插入
//因为目标节点前插入考虑到如果链表只有一个节点，那么这个插入操作就相当于头插，而头插需要改变头节点的位置，所以应当传二级指针
void InsertFront(SLNode** pphead, SLNode* pos, DataTypeSL x)
{
	assert(pphead);
	assert(pos);
	SLNode* cur = *pphead;
	if (cur == pos)
	{
		PushFrontSL(pphead, x);
		return;
	}
	while (cur->next != pos)
	{
		cur = cur->next;
	}
	SLNode* newNode = BuyNode(x);
	newNode->next = pos;
	cur->next = newNode;
}
//目标节点删除
void EraseFront(SLNode** pphead, SLNode** pos)
{
	assert(pphead);
	assert(*pphead);
	assert(pos);
	if (*pphead == *pos)
	{
		PopFrontSL(pphead);
	}
	else
	{
		SLNode* cur = *pphead;
		while (cur->next != (*pos))
		{
			cur = cur->next;
		}
		cur->next = cur->next->next;
		free(*pos);
		*pos = NULL;
	}
}

（2）带头循环双向链表实现

#define _CRT_SECURE_NO_WARNINGS 1
#include"List.h"
//创建新节点
ListNode* buyNode(LTDataType x)
{
	ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));
	if (newNode == NULL)
	{
		perror("malloc fail!");
		return NULL;
	}
	newNode->_data = x;
	newNode->_next = NULL;
	newNode->_prev = NULL;
	return newNode;
}
// 创建返回链表的头结点.
ListNode* ListCreate()
{
	ListNode* prehead = buyNode(-1);
	prehead->_next = prehead;
	prehead->_prev = prehead;
	return prehead;
}
// 双向链表销毁
void ListDestory(ListNode* pHead)
{
	ListNode* cur = pHead;
	cur = cur->_next;
	while (cur!=pHead)
	{
		ListNode* tmp = cur;
		cur = cur->_next;
		free(tmp);
	}
	free(pHead);
}
// 双向链表打印
void ListPrint(ListNode* pHead)
{
	ListNode* cur = pHead->_next;
	printf("prehead<==>");
	while (cur != pHead)
	{
		printf("%d<==>", cur->_data);
		cur = cur->_next;
	}
	printf("NULL");
	printf("\n");
}
// 双向链表尾插
void ListPushBack(ListNode* pHead, LTDataType x)
{
	assert(pHead);
	ListInsert(pHead, x);
	//ListNode* cur = pHead;
	//ListNode* tail = pHead->_prev;
	//ListNode* newNode = buyNode(x);
	//newNode->_next = cur;
	//cur->_prev = newNode;
	//tail->_next = newNode;
	//newNode->_prev = tail;
}
// 双向链表尾删
void ListPopBack(ListNode* pHead)
{
	assert(pHead);
	assert(pHead->_next != pHead);
	ListErase(pHead->_prev);
	//ListNode* cur = pHead;
	//ListNode* prevTail = cur->_prev->_prev;
	//ListNode* tail = cur->_prev;
	//pHead->_prev = prevTail;
	//prevTail->_next = cur;
	//free(tail);
}
// 双向链表头插
void ListPushFront(ListNode* pHead, LTDataType x)
{
	assert(pHead);
	ListInsert(pHead->_next, x);
	//ListNode* cur = pHead;
	//ListNode* head = cur->_next;
	//ListNode* newNode = buyNode(x);
	//newNode->_next = head;
	//newNode->_prev = cur;
	//cur->_next = newNode;
	//head->_prev = newNode;
}
// 双向链表头删
void ListPopFront(ListNode* pHead)
{
	assert(pHead);
	assert(pHead->_next != pHead);
	ListErase(pHead->_next);
	//ListNode* cur = pHead;
	//ListNode* head = cur->_next;
	//ListNode* nextHead = head->_next;
	//cur->_next = nextHead;
	//nextHead->_prev = cur;
	//free(head);
}
// 双向链表在pos的前面进行插入
void ListInsert(ListNode* pos, LTDataType x)
{
	assert(pos);
	ListNode* newNode = buyNode(x);
	ListNode* prevPos = pos->_prev;
	prevPos->_next = newNode;
	newNode->_prev = prevPos;
	pos->_prev = newNode;
	newNode->_next = pos;
}
// 双向链表删除pos位置的节点
void ListErase(ListNode* pos)
{
	ListNode* prevPos = pos->_prev;
	ListNode* nextPos = pos->_next;
	prevPos->_next = nextPos;
	nextPos->_prev = prevPos;
	free(pos);
}
// 双向链表查找
ListNode* ListFind(ListNode* pHead, LTDataType x)
{
	ListNode* cur = pHead->_next;
	while (cur != pHead)
	{
		if (cur->_data == x)
		{
			return cur;
		}
		cur = cur->_next;
	}
	return NULL;
}

（三）线性表应用（常见OJ题目）

数组相关OJ

1. 原地移除数组中所有的元素val，要求时间复杂度为O(N)，空间复杂度为O(1)。

思路：由于要求原地修改且时间复杂度为O（N），而顺序表的删除需要移动元素，所以不能采用常规的删除操作并且不能开辟新数组。

本题采用双指针的方法，一个指针p指向删除后所存放的有效数据，另一个指针q遍历数组

当 q所指向的元素不等于val时，将其赋给p指针指向的空间

需要注意的是，由于赋给p指针会覆盖掉原有的数据，所以被覆盖的数据都必须是已经判断过的数据，所以应当正向遍历。

int removeElement(int* nums, int numsSize, int val){
    int p=0;
    int q=0;
    while(p<numsSize&&q<numsSize)
    {
        if(nums[q]==val)
        {
            q++;
        }
        else
        {
            nums[p]=nums[q];
            p++;
            q++;
        }
    }
    return p;
}

2.合并两个有序数组。

算法思路：

由于nums1数组开辟的是两个数组合并后的空间，如果正向合并，那就必须要移动数据，那样的话复杂度就会增加，所以如果采用倒着遍历的方法来合并，由于nums1最后的位置为空，所以不用担心覆盖掉没有判断过的元素，所以使用三指针法

end1指向nums1的有效元素末位

end2指向nums2的有效元素末位

i指向nums1末位，用于将比较过的元素放入nums1中

通过比较end1 end2 以倒序的形式一个一个放入，有序是倒序判断倒序放入，所以不用担心覆盖的元素没有判断过。

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
    //倒着合并
    int end1=m-1;
    int end2=n-1;
    int i=m+n-1;
    while(end1 >= 0 && end2 >= 0)
    {
        if(nums1[end1] > nums2[end2])
        {
            nums1[i--] = nums1[end1--];
        }
        else
        {
            nums1[i--] = nums2[end2--];
        }
    }
    while(end2 >= 0)
    {
        nums1[i--] = nums2[end2--]; 
    }
}

链表相关OJ

1.反转链表

方法：画图

n3用于保存反转之前两个节点后的节点，防止反转后找不到了

注意： n1 n2是负责反转的指针，只有当n1 n2 指向最后两个节点并且完成指针改向后，才能算完成反转，如果当n3指向NULL时循环停止，那么此时最后一次反转就无法完成，所以只有当n2指向NULL时才表示最后一次反转已经完成，操作n3时注意判断空指针

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

//改变指针指向法（三指针法）
struct ListNode* reverseList(struct ListNode* head){
    if(head==NULL)return NULL;
    struct ListNode* n1 = NULL;
    struct ListNode* n2 = head; 
    struct ListNode* n3 = head->next;
    while(n2)
    {
        n2->next = n1;
        //迭代
        n1 = n2;
        n2 = n3;
        if(n3)
            n3 = n3->next;
    }
    return n1;
}

2.给定一个带有头结点 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则 返回第二个中间结点。

方法：快慢指针，一个一次走一步，一个一次走两步

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* middleNode(struct ListNode* head){
    if(head==NULL||head->next==NULL)
    {
        return head;
    }
    struct ListNode* slow=head;
    struct ListNode* fast=head;
    while(fast!=NULL&&fast->next!=NULL)
    {
        slow=slow->next;
        fast=fast->next->next;
    }
    return slow;
}

3.将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。

方法：利用哨兵位头节点可以让合并的尾插更加便捷，不需要通过判断两个链表头节点谁大谁小来确定头节点

注意：1.释放头节点空间

           2.当一个链表为空时，剩下的链表只需要将剩下链表的头节点连到合并后的链表尾部即可，不用一个一个连。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

struct ListNode* buyNode(int x)
{
    struct ListNode* plist=(struct ListNode*)malloc(sizeof(struct ListNode));
    if(plist==NULL)
    {
        perror("malloc fail");
		return NULL;
    }
    plist->val=x;
    plist->next=NULL;
    return plist;
}
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2){
    if(list1==NULL)return list2;
    if(list2==NULL)return list1;
    struct ListNode* prehead = buyNode(-1);
    struct ListNode* cur=prehead;
    while(list1!=NULL&&list2!=NULL)
    {
        if(list1->val<=list2->val)
        {
            cur->next=list1;
            list1=list1->next;
        }
        else
        {
            cur->next=list2;
            list2=list2->next;
        }
        cur=cur->next;
    }
    if(list2!=NULL)
    {
        cur->next=list2;
    }
    else
    {
        cur->next=list1;
    }
    list1=prehead->next;
    free(prehead);
    return list1;
}

4.编写代码，以给定值x为基准将链表分割成两部分，所有小于x的结点排在大于或等于x的结点之前 。

思路：1.利用哨兵位可以避免判断空指针的麻烦

           2.可以设置头指针和尾指针，便于对链表的控制

           3.大体思路就是将大于等于目标值的节点尾插组成一个新链表，再将小于目标值的节点组成一个新链表，再将两个链表链接

           4.由于是用小于目标值的链表链接大于目标值的链表，所以小于目标值的尾节点原本的next会被更改，但是大于目标值的链表的尾节点的next还连接着原来链表中的节点，需要置空。

           注意：链表题不要怕设置指针变量，多设置几个指针变量有时可以减少很多麻烦

class Partition {  
public:
    ListNode* partition(ListNode* pHead, int x) {
        struct ListNode * pless ;
        pless= (struct ListNode *)malloc(sizeof(struct ListNode));
        struct ListNode * pgreater;
        pgreater = (struct ListNode *)malloc(sizeof(struct ListNode));
        struct ListNode * lesstail = pless;
        struct ListNode * greatertail = pgreater;
        struct ListNode * cur = pHead;
        while (cur) {
            if (cur->val < x) {
                lesstail->next = cur;
                lesstail = lesstail->next;
            } else {
                greatertail->next = cur;
                greatertail = greatertail->next;
            }
            cur=cur->next;
        }
        lesstail->next=pgreater->next;
        greatertail->next=NULL;
        pHead=pless->next;
        free(pgreater);
        free(pless);
        return pHead;
    }
};

5.链表的回文结构。

思路：

1.找到链表的中间节点

2.反转后半段链表

3.前半段从头开始，后半段从原本链表的尾开始遍历，比较前后半段值是否相等

struct ListNode* reverse(struct ListNode* head){
    if(head==NULL||head->next==NULL)return head;
    struct ListNode* n1=NULL;
    struct ListNode* n2=head;
    struct ListNode* n3=head->next;
    while(n2)
    {
        n2->next=n1;
        n1=n2;
        n2=n3;
        if(n3)
        {
            n3=n3->next;
        }
    }
    return n1;
}
//找到中间节点
struct ListNode* findMid(struct ListNode* head)
{
    struct ListNode* slow=head;
    struct ListNode* fast=head;
    while(fast!=NULL&&fast->next!=NULL)
    {
        slow=slow->next;
        fast=fast->next->next;
    }
    return slow;
}
class PalindromeList {
public:
    bool chkPalindrome(ListNode* head) {
        struct ListNode* cur=findMid(head);
        cur=reverse(cur);
        struct ListNode* phead=head;
        struct ListNode* tail=cur;
        while(phead!=NULL&&tail!=NULL)
        {
            if(phead->val!=tail->val)
            {
                return false;
            }
            phead=phead->next;
            tail=tail->next;
        }
        return true;
    }
};

6.输入两个链表，找出它们的第一个公共结点。

思路：计算出两个链表的长度，定义两个指针分别指向两个链表的头节点，让长的链表先走出长度差，然后两个指针再一起走并判断指向的节点地址是否一致。

注意： 判断的是否相交是判断两个指针指向的地址是否相同。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    int l1=0;
    int l2=0;
    struct ListNode* n1=headA;
    struct ListNode* n2=headB;
    while(n1)
    {
        n1=n1->next;
        l1++;
    }
    while(n2)
    {
        n2=n2->next;
        l2++;
    }
    n1=headA;
    n2=headB;
    if(l1>l2)
    {
        while(l1-l2)
        {
            
            n1=n1->next;
            l1--;
        }
    }
    else if(l1<l2)
    {
        while(l2-l1)
        {
            n2=n2->next;
            l2--;
        }
    }
    while(n1!=NULL&&n2!=NULL&&n1!=n2)
    {
        n1=n1->next;
        n2=n2->next;
    }
    if(n1==NULL||n2==NULL)return NULL;
    return n1;
}

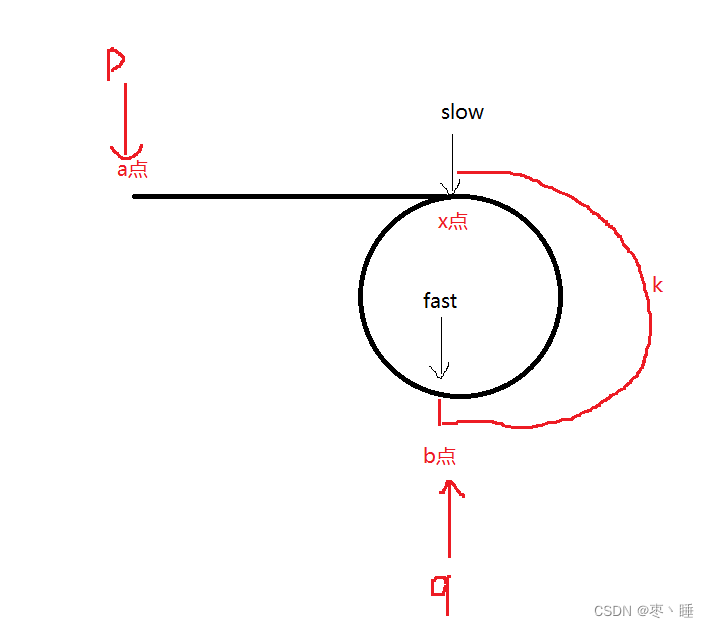
7.给定一个链表，返回链表开始入环的第一个结点。 如果链表无环，则返回 NULL

结论

让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环

运行，两个指针都是每次均走一步，最终肯定会在入口点的位置相遇。

证明：

 

 

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* fast=head;
    struct ListNode* slow=head;
    struct ListNode* cur=head;
    while(fast!=NULL&&fast->next!=NULL)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)
        {
            while(fast!=cur)
            {
                fast=fast->next;
                cur=cur->next;
            }
            return cur;
        }
    }
    return NULL;
}

8.给定一个链表，每个结点包含一个额外增加的随机指针，该指针可以指向链表中的任何结点或空结点。 要求返回这个链表的深度拷贝。

基本思路：

1.把复制链表的节点，每个都插入到原链表对应节点的后面

2.通过拼接成的新链表，确定出复制链表random对应的节点

3.摘出复制链表，还原原链表 

注意：画图画图画图！！！

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *next;
 *     struct Node *random;
 * };
 */


/*
    基本思路：
    1.把复制链表的节点，每个都插入到原链表对应节点的后面
    2.通过拼接成的新链表，确定出复制链表random对应的节点
    3.摘出复制链表，还原原链表
*/
struct Node* buyNode(int x)
{
    struct Node* newnode=(struct Node*)malloc(sizeof(struct Node));
    newnode->val=x;
    newnode->next=NULL;
    newnode->random=NULL;
    return newnode;
}
struct Node* copyRandomList(struct Node* head) {
    if(head==NULL)return NULL;
	struct Node* cur=head;
    struct Node* tmp=head;
    //1.把复制链表的节点，每个都插入到原链表对应节点的后面
    while(cur)
    {
        tmp=cur->next;
        cur->next=buyNode(cur->val);
        cur->next->next=tmp;
        cur=tmp;
    }
    // 2.通过拼接成的新链表，确定出复制链表random对应的节点
    cur=head;
    while(cur)
    {
        struct Node* copy=cur->next;
        if(cur->random==NULL)
        {
            copy->random=NULL;
        }
        else
        {
            copy->random=cur->random->next;
        }
        cur=copy->next;
    }
    //3.摘出复制链表，还原原链表
    struct Node* prehead=buyNode(-1);
    cur=head;
    tmp=head->next;
    struct Node* newList=prehead;
    while(cur)
    {
        newList->next=tmp;
        newList=newList->next;
        cur->next=tmp->next;
        cur=cur->next;
        if(cur!=NULL)
        {
            tmp=cur->next;
        }
       
        
    }
    struct Node* result=prehead->next;
    free(prehead);
    return result;
}