数学名词：

丁兰子

已于 2024-01-19 17:28:14 修改

阅读量424

点赞数 8

文章标签：学习 nlp

于 2024-01-12 20:02:37 首次发布

本文链接：https://blog.youkuaiyun.com/m0_58758292/article/details/135560921

版权

本文介绍了数学刻画的概念，重点阐述了洛必达法则在解决微积分中的不定型极限问题，如求解极限、导数计算、微分方程、渐近线、无穷级数等方面的应用实例，以及导数的通俗解释和计算方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数学刻画

数学刻画是指用数学的语言、符号和方法来描述或表达某种概念、现象或对象。通俗来讲，就是用数学的方式来描绘描述某个事物或者概念。例如，通过方程式、图表、函数等数学工具，来描述和表达现实世界中的各种关系和规律。数学刻画可以帮助人们更准确地理解和分析事物的特性、变化规律等。

洛必达法则

洛必达法则是微积分中的一个定理，用于处理一些形式为"0/0"或"∞/∞"的不定型极限问题。洛必达法则指出，在某些条件下，原极限问题可以转化为其导数的极限问题，从而得以求解。

以下是一些使用洛必达法则的场景：

1. 求解极限问题：例如，求解极限 $\lim_{x->0} [\frac{sin(x)}{x}]$ 。这是一个“0/0”形式的不定型极限，可以通过洛必达法则求解。

2. 导数的计算：例如，求解 $f(x) = ln(x)$ 的导数。通过洛必达法则，我们可以首先将问题转化为求解极限 $\lim_{h->0}[(ln(x+h) - \frac{ln(x)}{h}]$ ，然后通过洛必达法则求解。

3. 微分方程的求解：例如，求解微分方程 $\frac{dy}{dx }=\frac{y}{x}$ 。通过洛必达法则，我们可以将问题转化为求解极限 $\lim_{x->0}[\frac{y(x)}{x}]$ ，然后通过洛必达法则求解。

4. 求解渐近线：例如，求解函数f $f(x) = \frac{e^x}{x}$ 的水平渐近线。通过洛必达法则，我们可以求解极限 $\lim_{x->\infty }$ $\frac{e^x}{x}$ ，从而确定函数的渐近线。

5. 求解无穷级数：例如，求解级数 $\sum\frac{1}{n^2}$ 。通过洛必达法则，我们可以求解极限 $\lim_{n->\infty } [\frac{1}{n^2}]$ ，从而确定级数的收敛性。

6. 求解函数的极限：例如，求解极限 $\lim_{x->0} [\frac{(e^x - 1)}{x}]$ 。这是一个“0/0”形式的不定型极限，可以通过洛必达法则求解。

7. 求解复杂的极限：例如，求解极限lim(x->0) [(sin(x) - x) / x^3]。这是一个复杂的不定型极限，可以通过多次应用洛必达法则求解。

8. 求解多变量函数的极限：例如，求解极限 $\lim_{x,y->0}[\frac{(\mathrm{x^2}y)}{(x^2 + y^2)}]$ 。这是一个多变量函数的不定型极限，可以通过洛必达法则求解。

9. 求解函数的不定型积分：例如，求解积分 $\int_{0 \to \infty }[\frac{x}{(e^x - 1)}] dx$ 。这是一个不定型积分，可以通过洛必达法则求解。

10. 在物理、工程和经济等领域的实际问题中应用洛必达法则：例如，在物理学中，求解电荷分布的极限问题；在经济学中，求解边际成本的极限问题；在工程学中，求解材料应力的极限问题。

导数

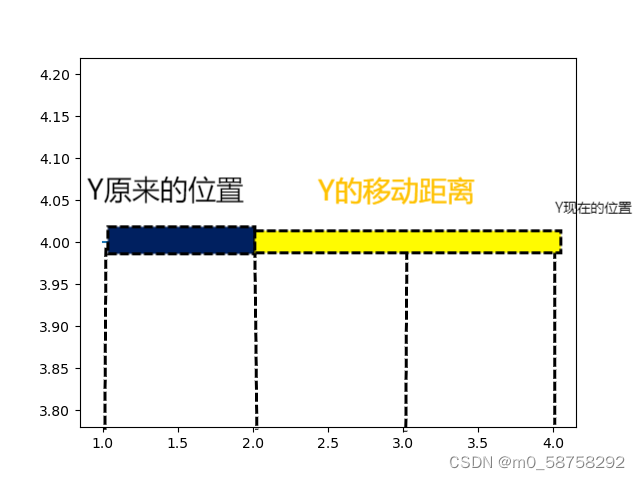
用通俗话描述导数：（相对运动）当X静止不动时，Y的移动距离

举例：y = x^n (n为实数)，导数为 y' = n*x^(n-1)


def fun(x, n):
    y = x ** n  # 函数y
    k = n * x ** (n - 1)  # 导数
    y_1 = y + k + 1
    print(f'当前Y值；=============={y}\n当X不动时Y移动了：{k}\n 根据导数预测下一个Y值为：{y_1}')


if __name__ == '__main__':
    fun(1, 2)
    fun(2, 2)

# 输出：
# 当前Y值；==============1
# 当X不动时Y移动了：2   所以 y=1**2的导数为2
#  根据导数预测下一个Y值为：4
# 当前Y值；==============4
# 当X不动时Y移动了：4
#  根据导数预测下一个Y值为：9