剑指offer(简单)

剑指 Offer 03. 数组中重复的数字

方法1:借助HashSet

利用HashSet的数据结构特点---HashSet中存储的都是不重复的元素.遍历数组把元素存储到HashSet中,判断如果这个元素已经在HashSet中了,就代表遇到重复的数字了,就可以直接返回
class Solution {
    public int findRepeatNumber(int[] nums) {
        Set<Integer> set=new HashSet<>();
        for(int num:nums){
            if(set.contains(num)){
                return num;
            }
            set.add(num);
        } 
        return -1;
    }
}
-------------------------------------------------------------------------------------------------------------------------

方法2:使用Arrays类对数组进行排序

使用Arrays.sort(数组名)对数组进行升序排序,然后遍历数组,如果相邻下标的元素一样就代表遇到重复的数字了,就可以直接返回
class Solution {
    public int findRepeatNumber(int[] nums) {
        Arrays.sort(nums);
        int i=0;
        for(;i<nums.length-1;i++){
            if(nums[i]==nums[i+1]){
                break;
            }
        }
        return nums[i];
    }
}

替换空格

剑指offer05.替换空格

方法1:借助StringBuilder

首先算出s中的空格数,然后新建一个StringBuilder类型的字符串str,让其存放s中的内容.

保存当前str的长度oldL,然后计算空格变成%20的新str的长度newL,之后将str的长度更新为newL.

新建两个变量i和j分别代表oldL时str的最后一个元素的下标,以及newL时str的最后一个元素的下标.通过while循环控制i和j的边界.

下面开始在while循环中判断:

如果i下标的元素不是空格,那么把i下标的元素赋给j下标的元素,然后i--和j--.

如果i下标的元素是空格,那么对j下表进行'0'赋值,然后j--,紧接着'2'赋值,然后j--,紧接着'%'赋值,然后j--,最后i--一次.当while循环结束,此时str就已经是输出要的样子了.

但是还差一步,因为返回值类型是String,因此还要再返回的时候把str转换成String类型的.
class Solution {
    public String replaceSpace(String s) {
        if(s.length()==0){
            return "";
        }
        int count=0;
        for(char ch:s.toCharArray()){
            if(ch==' '){
                count++;
            }
        }
        StringBuilder str=new StringBuilder(s);
        int oldL=str.length();
        int newL=oldL+2*count;
        str.setLength(newL);
        int i=oldL-1;
        int j=newL-1;
        while(i>=0 && j>=0){
            if(str.charAt(i)!=' '){
                str.setCharAt(j--,str.charAt(i--));
            }
            else{
                str.setCharAt(j--,'0');
                str.setCharAt(j--,'2');
                str.setCharAt(j--,'%');
                i--;
            }
        }
        return str.toString();
    }
}

从尾到头打印链表

剑指 Offer 06. 从尾到头打印链表

方法1:翻转链表,并记录链表长度.之后新创建一个长度为链表长度的数组,把反转的链表中的节点值依次放入数组中,最后返回数组.

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    int len;
    public int[] reversePrint(ListNode head) {
        if(head==null){
            return new int[0];
        }
        ListNode newHead=reverseL(head);
        int[] arr=new int[len];
        for(int i=0;i<arr.length;i++){
            arr[i]=newHead.val;
            newHead=newHead.next;
        }
        return arr;
    }
    public ListNode reverseL(ListNode head){
        ListNode pre=null;
        while(head!=null){
            ListNode headN=head.next;
            head.next=pre;
            pre=head;
            head=headN;
            len++;
        }
        return pre;
    }
}

-------------------------------------------------------------------------------------------------------------------------

方法2:递归法

先递归走至链表末端，回溯时依次将节点值加入ArrayList ，这样就可以实现链表值的倒序输出.

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    List<Integer> tmp=new ArrayList<>();
    public int[] reversePrint(ListNode head) {
        reverseL(head);
        int[] arr=new int[tmp.size()];
        for(int i=0;i<arr.length;i++){
            arr[i]=tmp.get(i);
        }
        return arr;
    }
    void reverseL(ListNode head){
        if(head==null){
            return;
        }
        reverseL(head.next);
        tmp.add(head.val);
    }
}

-------------------------------------------------------------------------------------------------------------------------

方法3:辅助栈法(使用LinkedList)

class Solution {
    public int[] reversePrint(ListNode head) {
        LinkedList<Integer> stack = new LinkedList<Integer>();
        while(head != null) {
            stack.addLast(head.val);
            head = head.next;
        }
        int[] res = new int[stack.size()];
        for(int i = 0; i < res.length; i++)
            res[i] = stack.removeLast();
    return res;
    }
}

用两个栈实现队列

剑指 Offer 09. 用两个栈实现队列

方法1:使用两个Stack实现一个队列
class CQueue {
    Stack<Integer> stack1;
    Stack<Integer> stack2;
    public CQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }
    
    public void appendTail(int value) {
        stack1.push(value);
    }
    
    public int deleteHead() {
        if(stack1.isEmpty() && stack2.isEmpty()){
            return -1;
        }
        if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */
-------------------------------------------------------------------------------------------------------------------------

方法2:使用两个LinkedList模拟两个栈实现一个队列
class CQueue {
    LinkedList<Integer> A,B;
    public CQueue() {
        A=new LinkedList<>();
        B=new LinkedList<>();
    }
    
    public void appendTail(int value) {
        A.addLast(value);
    }
    
    public int deleteHead() {
        if(A.isEmpty() && B.isEmpty()){
            return -1;
        }
        if(B.isEmpty()){
            while(!A.isEmpty()){
                B.addLast(A.removeLast());
            }
        }
        return B.removeLast();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */
来自一位大佬的观点:Java 中的 stack 是一个过时的框架，一般不建议使用，因此没有用~ 并且，诸如 Python 这样的语言，就没有 stack 这种概念，一个 [] 既可以当栈、也可以当队列，因此也是同样的问题。

Stack，ArrayDeque，LinkedList的区别_cartoon23333的博客-优快云博客

JAVA 栈，为什么要使用Deque，而不推荐使用Stack，Deque中ArrayDeque与LinkedList的区别，Deque方法详解_俩只猴的博客-优快云博客_deque 和linkedlist

斐波那契数列

剑指 Offer 10- I. 斐波那契数列

方法1:

class Solution {
    public int fib(int n) {
        if(n==0 || n==1){
            return n;
        }
        int f0=0;
        int f1=1;
        int f2=f0+f1;
        while(n>2){
            f0=f1;
            f1=f2;
            f2=(f0+f1)%1000000007;
            n--;
        }
        return f2;
    }

}

-------------------------------------------------------------------------------------------------------------------------

方法2:动态规划

class Solution {
    public int fib(int n) {
        if(n==0 || n==1){
            return n;
        }
        int[] dp=new int[n+1];
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i]=(dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
}

青蛙跳台阶问题

剑指 Offer 10- II. 青蛙跳台阶问题

此类求 多少种可能性 的题目一般都有 递推性质 ，即 f(n) 和 f(n−1)…f(1) 之间是有联系的。

设跳上n级台阶有f(n)种跳法,在所有跳法中,青蛙的最后一步只有两种情况:跳上1级台阶或跳上2级台阶 .

当最后一步为1级台阶的时候:剩下n-1级台阶,这种情况共有f(n-1)种跳法

当最后一步为2级台阶的时候,剩下n-2级台阶,这种情况共有的f(n-2)种跳法

f(n)=f(n-1)+(n-2)

分析到这里你有没有什么发现?

其实青蛙跳台阶问题的解决思路可以转化为求斐波那契数列第n项的值,唯一不同的事其实数字不同.

青蛙跳台阶问题:f(0)=1,f(1)=1,f(2)=2

斐波那契数列问题:f(0)=0,f(1)=1,f(2)=1

方法1:
class Solution {
    public int numWays(int n) {
        if(n==0 || n==1){
            return 1;
        }
        int f0=1;
        int f1=1;
        int f2=f0+f1;
        while(n>2){
            f0=f1;
            f1=f2;
            f2=(f0+f1)%1000000007;
            n--;
        }
        return f2;
    }
}
-------------------------------------------------------------------------------------------------------------------------

方法2:动态规划
class Solution {
    public int numWays(int n) {
        if(n==0 || n==1){
            return 1;
        }
        int[] dp=new int[n+1];
        dp[0]=1;
        dp[1]=1;
        int i=2;
        for(;i<=n;i++){
            dp[i]=(dp[i-1]+dp[i-2])%1000000007;
        }
        return dp[n];
    }
}

旋转数组的最小数字

剑指 Offer 11. 旋转数组的最小数字

排序数组的查找问题首先考虑使用 二分法 解决，其可将 遍历法 的 线性级别 时间复杂度降低至 对数级别

方法1:二分法

1.首先创建两个变量i和j分别指向数组左右两端

2.然后开始循环使用二分法,创建m变量为二分的中点,m=(i+j)/2

3.我们让每次二分查找都是numbers[m]和numbers[j]进行比较

numbers[m]和numbers[j]的大小关系可分为三种情况:

(1)numbers[m]>numbers[j]:m一定在左排序数组中,此时旋转点x一定在[m+1,j]区间中,此时执行i=m+1

(2)numbers[m]<numbers[j]:m一定在右排序数组中,此时旋转点x一定在[i,m]区间中,此时执行j=m

(3)numbers[m]=numbers[j]:无法判断m在那个排序数组中,那么也就无法判断旋转点x在[i,m]

区间中,还是在[m+1,j]区间中.那么这种情况说明至少一定在[i,m]区间所有元素相等或者[m+1,j]区间中所有元素相等.针对这种情况,我们就不使用二分查找了,而是使用线性查找

4.返回返回值

(1)当出现上面的第三种情况,那么找到了以后就可以返回了

(2)当一直是前两种情况时,最终循环条件不满足(i=j的时候)就会跳出循环,然后返回旋转点的值
class Solution {
    public int minArray(int[] numbers) {
        int i=0;
        int j=numbers.length-1;
        while(i<j){
            int m=(i+j)/2;
            if(numbers[m]>numbers[j]){
                i=m+1;
            }
            else if(numbers[m]<numbers[j]){
                j=m;
            }
            else{
                int x=i;
                for(int k=i+1;k<j;k++){
                    if(numbers[k]<numbers[x]){
                        x=k;
                    }
                }
                return numbers[x];
            }
        }
        return numbers[i];
    }
}

二进制中的1的个数

剑指 Offer 15. 二进制中1的个数

方法1:逐位判断

让n与1进行与运算,即n&1.

根据与运算特点,如果n&1=0,那么代表n二进制最右一位为0;如果n&1=1,那么代表n二进制最右一位为1.

创建一个变量count来计数n中有多少1.----->count+=n&1

进行完一次与运算就让n右移一位,另外因为本题要求把n看做无符号数,因此使用无符号右移(>>>)

结束条件是n==0的时候
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
        while(n!=0){
            count+=n&1;
            n>>>=1;
        }
        return count;
    }
}
-------------------------------------------------------------------------------------------------------------------------

方法2:巧用n&(n-1)
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count=0;
        while(n!=0){
            n=n&(n-1);
            count++;
        }
        return count;
    }
}

打印从1到最大的n位数

剑指 Offer 17. 打印从1到最大的n位数

由于这道题他的返回值类型是int[],相当于默认所有数字都在 int32 整型取值范围内，那么就不需要考虑大数越界问题,因此这道题才会被归为简单题.

方法1:

如果n是1,那么就需要打印1-9

如果n是2,那么就需要打印1-99

如果n是3,那么就需要打印1-999

...

找规律,发现最大的n位数可以总结为:10^n-1

这样就好办了,创建一个数组,长度就是最大的n位数

然后把从1到最大的n位数一次放入数组中
class Solution {
    public int[] printNumbers(int n) {
        int end = (int)Math.pow(10, n) - 1;
        int[] res = new int[end];
        for(int i = 0; i < end; i++)
            res[i] = i + 1;
        return res;
    }
}
-------------------------------------------------------------------------------------------------------------------------

上面有提到大数越界问题,如果这道题是考虑大数越界的情况呢?参考这个大佬写的

面试题17. 打印从 1 到最大的 n 位数（分治算法 / 全排列)

删除链表的节点

剑指 Offer 18. 删除链表的节点

方法1:单指针
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode deleteNode(ListNode head, int val) {
        if(head==null){
            return null;
        }
        if(head.val==val){
            return head.next;
        }
        ListNode cur=head;
        while(cur.next!=null && cur.next.val!=val){
            cur=cur.next;
        }
        if(cur.next!=null){
            cur.next=cur.next.next;
        }
        return head;
    }
}
-------------------------------------------------------------------------------------------------------------------------

方法2:双指针

思路和单指一样,但是单指针就能搞定的事,好像就可以不劳烦双指针了,这里就不写代码了

调整数组顺序使奇数位于偶数前面

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面

方法1:双指针

创建两个变量i和j,分别放置到0下标和nums.length-1下标

i下标用来判断从前往后走遇到的元素是否时偶数

j下标用来判断从后往前走遇到的元素是否是奇数

两种情况:

(1)当i下标的元素偶数且j下标的元素是奇数时,交换i下标和j下标的元素,然后i++,j--

(2)当i下标的元素是奇数,i++;当j下标的元素时偶数,j--

终止条件是当循环不满足i<j时,跳出循环
class Solution {
    public int[] exchange(int[] nums) {
        if(nums.length==0){
            return new int[0];
        }
        int i=0;
        int j=nums.length-1;
        while(i<j){
            while(i<j && (nums[i]&1)==1){
                i++;
            }
            while(i<j && (nums[j]&1)==0){
                j--;
            }
            int tmp=nums[i];
            nums[i]=nums[j];
            nums[j]=tmp;
        }
        return nums;
    }
}

链表中倒数第k个节点

剑指 Offer 22. 链表中倒数第k个节点

方法1:双指针

创建两个变量fast和slow起始于head节点,fast先走(k-1)步,然后fast和slow一人一步走

具体:

1.注意一些边界判断:head是否为null;k<=0吗;k是否超出链表长度(这个是在fast先走(k-1)步的时候同时判断的,如果判断k超出了,那么就当下返回(你如果觉得不好想,可以举这个例子:链表就是上面示例的12345,然后k是6)

2.上面都边界判断完成且通过,下面就来到fast和slow一人一步走阶段,但需注意循环的条件是fast.next!=null.这个真的得想清楚,我一开始没通过就是这里出了问题,写成fast!=null.(可以就拿上面示例12345,k=2去想)

3.最后返回的是slow所在的节点
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        if(head==null || k<=0){
            return null;
        }
        ListNode fast=head;
        int zz=k-1;
        while(zz!=0 && fast!=null){
            fast=fast.next;
            zz--;
        }
        if(fast==null){
            return null;
        }
        ListNode slow=head;
        while(fast.next!=null){
            slow=slow.next;
            fast=fast.next;
        }
        return slow;
    }
}
方法2:双指针

虽说方法1和方法2都是使用双指针,但是具体实现细节和方法1不一样,看你更理解哪个吧

具体:

1.专门算出来链表的长度,然后依旧是各种边界判断:head是否为null;k是否超出链表长度;k<=0吗

2.当上面所有的边界判断都完成后,就创建fast和slow,然后先是fast走k步,然后当fast!=null时,fast和slow一人一步走(注意这里是fast是先走k步,以及后面的限制条件是fast!=null,看清楚想清楚为什么很重要,不然下次做到这题还是不会!!!!)

3.返回slow所在的节点
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        if(head==null){
            return null;
        }
        if(k>sizeOfHead(head) || k<=0){
            return null;
        }
        ListNode fast=head;
        ListNode slow=head;
        while(k!=0){
            fast=fast.next;
            k--;
        }
        while(fast!=null){
            fast=fast.next;
            slow=slow.next;
        }
        return slow;
    }
    public int sizeOfHead(ListNode head){
        ListNode cur=head;
        int count=0;
        while(cur!=null){
            count++;
            cur=cur.next;
        }
        return count;
    }
}

反转链表

剑指 Offer 24. 反转链表

方法1:不带傀儡节点

这种方法比方法2要难想一点,换句话说你可以先学会方法2,再来攻方法1

具体:

1.注意边界限制:head是否为null

2.创建两个变量cur和curN,分别设置在head节点和head.next节点上

3.注意循环限制条件(你可以就拿示例去想),循环中再创建一个变量curNN,作为curN.next的节点上的变量(想想为什么.是不是因为我翻转节点指向以后我需要知道下一个节点在哪儿啊,curNN就是来提前保存下一个节点的),然后就往后移吧

4.跳出循环后,这时链表已经反转完成了,但是!!!还差非常关键的一步,这步没有注意到就功亏一篑啊!!!这一步就是:将head节点的指向指为null

这一步我真的醉了,我做过好多次反转链表,但是老是忘记这一步,或者说刚看到这道题的时候还想着呢,等代码写到这里就忘得一干二净了

如果忘了这一步就会出现这种情况:
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null){
            return null;
        }
        ListNode cur=head;
        ListNode curN=cur.next;
        while(curN!=null){
            ListNode curNN=curN.next;
            curN.next=cur;
            cur=curN;
            curN=curNN;
        }
        head.next=null;
        return cur;
    }
}
方法2:带傀儡节点

方法2之所以比方法1好想,重点就在这个傀儡节点上

有了这个傀儡节点,代码和思路就好想,不容易出错

另外也不需要在代码的最后提醒自己不能忘记给head指向null,因为傀儡节点在开头的时候就让head指向null了
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null){
            return null;
        }
        ListNode pre=null;
        ListNode cur=head;
        while(cur!=null){
            ListNode curN=cur.next;
            cur.next=pre;
            pre=cur;
            cur=curN;
        }
        return pre;
    }
}

合并两个排序的链表

剑指 Offer 25. 合并两个排序的链表

方法1:傀儡节点

我这里是按照两个链表l1,l2中节点值如果想等,走l1,你如果想反过来也完全没问题

创建一个傀儡节点pre,只是多少无所谓,我这里设的是-1

紧接着再创建一个变量cur从这个傀儡节点开始

接下来进入循环,循环限制条件是两个链表走到的节点都不能为空,然后有这么两种情况:

1.如果l1.val<=l2.val,cur.next指向l1,然后cur走到l1,l1走到l1.next

2.如果l1.val>l2.val,cur.next指向l2,然后cur走到l2,l2走到l2.next

跳出循环说明要么走完,要么有不符合条件的选项,那么我们一个个来判断

1.如果此时l1!=null,那么就直接让pre指向l1

2.如果此时l2!=null,那么就直接让pre指向l2

最后返回返回值pre.next
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1==null && l2==null){
            return null;
        }
        if(l1==null){
            return l2;
        }
        if(l2==null){
            return l1;
        }
        ListNode pre=new ListNode(-1);
        ListNode cur=pre;
        while(l1!=null && l2!=null){
            if(l1.val<=l2.val){
                cur.next=l1;
                cur=l1;
                l1=l1.next;
            }
            else{
                cur.next=l2;
                cur=l2;
                l2=l2.next;
            }
        }
        if(l1!=null){
            cur.next=l1;
        }
        if(l2!=null){
            cur.next=l2;
        }
        return pre.next;
    }
}

二叉树的镜像

剑指 Offer 27. 二叉树的镜像

方法1:递归法

1.首先是判断边界:root是不是为null,同时这里这个边界条件也是之后递归的终止条件

2.接下来进行递归,先递归左子树到叶子节点,然后进行递归右子树

3.这个时候当前root的左子树和右子树的值拿到了,就可以交换左右子树的值

4.返回root进行回溯,这个root返回给上一级递归中的leftT,然后紧接着进行上一级递归的剩下流程...依次往上回溯

5.最终整个人二叉树完成镜像
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root==null){
            return null;
        }
        TreeNode leftT=mirrorTree(root.left);
        TreeNode rightT=mirrorTree(root.right);
        root.left=rightT;
        root.right=leftT;
        return root;
    }
}

对称的二叉树

剑指 Offer 28. 对称的二叉树

方法1:递归法

题目要求判断一颗二叉树是不是对称的,重点在你怎么去理解对称,怎么根据"对称"的特点想到解决方案

具体:

1.还是判断边界:root是否为null

2.兵分两路,root.left和root.right

3.递归的一些终止条件要想全:

3.1如果root1==null && root2==null那么代表结构和值都是对称的,返回true

3.2如果root1==null || root2==null那么代表结构是不对称的,返回false

3.3如果root1.val!=root2.val那么代表值是不对称的,返回false

4.进行递归:

递归让root1.left和root2.right比较

之后递归让root1.right和root2.left比较

然后这个时候到终止条件了,开始回溯

由于这道题是判断对称,因此回溯的时候的条件是上面两个递归结果的与运算(&&)

重点是这里面递归的思想要想清楚,回溯也是.递归如果只在脑子中把图展开如果觉得难想的话,建议画图,虽然麻烦,但思路清晰
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null){
            return true;
        }
        return isSymmetric2(root.left,root.right);
    }
    public boolean isSymmetric2(TreeNode root1,TreeNode root2){
        if(root1==null && root2==null){
            return true;
        }
        if(root1==null || root2==null){
            return false;
        }
        if(root1.val!=root2.val){
            return false;
        }
        boolean lr=isSymmetric2(root1.left,root2.right);
        boolean rl=isSymmetric2(root1.right,root2.left);
        return lr && rl;
    }
}

顺时针打印矩阵

剑指 Offer 29. 顺时针打印矩阵

方法1:模拟

根据题目给的示例可以发现,顺时针打印矩阵的顺序是:

从左至右-->从上至下-->从右至左-->从下至上的循环

得出这个结论之后,我们可以设定矩阵的"左、上、右、下“四个边界，通过模拟矩阵遍历顺序来解决此题

具体：

1.首先是判断边界：matrix是否为空

2.创建四个边界并赋予他们初始值

3.创建一维数组res，设定长度（矩阵的长*宽）

4.按照从左至右-->从上至下-->从右至左-->从下至上的顺序进行循环遍历

4.1根据边界遍历，并将遍历到的元素添加到res中

4.2边界向内收敛1，并判断边界是否相遇（相遇代表：如果左边界大于右边界、上边界大于下边界、右边界小于左边界、下边界小于上边界），那么就跳出循环

5.返回数组res
class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if(matrix.length==0){
            return new int[0];
        }
        int left=0;
        int right=matrix[0].length-1;
        int top=0;
        int bottom=matrix.length-1;
        int[] res=new int[matrix[0].length*matrix.length];
        int x=0;
        while(true){
            for(int i=left;i<=right;i++){
                res[x++]=matrix[top][i];
            }
            if(++top>bottom){
                break;
            }
            for(int i=top;i<=bottom;i++){
                res[x++]=matrix[i][right];
            }
            if(--right<left){
                break;
            }
            for(int i=right;i>=left;i--){
                res[x++]=matrix[bottom][i];
            }
            if(--bottom<top){
                break;
            }
            for(int i=bottom;i>=top;i--){
                res[x++]=matrix[i][left];
            }
            if(++left>right){
                break;
            }
        }
        return res;
    }
}

包含min函数的栈

剑指 Offer 30. 包含min函数的栈

方法1:辅助栈

使用两个栈来完成

具体:

1.对于push:

一个栈(nmStack)用来正常放push的x

另一个栈(minStack)用来只放当前最小值

对于minStack,怎么判断并一直放当前最小值呢:如果minStack为空,那么直接push当前的x;如果不为空,那么就需要让minStack.peek()和x作比较,如果minStack.peek()的值大于等于x,我们就push当前的x进入minStack,如果minStack.peek()的值小于x,那么就push当前minStack.peek()的值进入minStack

2.对于pop:

两个栈需要做到一致,因此两个都要pop()

3.对于top:

这个top就是peek的意思

你如果不知道该top谁,可以看示例中它top的时候top的是谁,看完后能发现top的是nmStack

4.对于min:

就是minStcak.peek()
class MinStack {
    Stack<Integer> nmStack;
    Stack<Integer> minStack;
    /** initialize your data structure here. */
    public MinStack() {
        nmStack=new Stack<>();
        minStack=new Stack<>();
    }
    
    public void push(int x) {
        nmStack.push(x);
        if(minStack.isEmpty() || minStack.peek()>=x){
            minStack.push(x);
        }
        else{
            minStack.push(minStack.peek());
        }
    }
    
    public void pop() {
        minStack.pop();
        nmStack.pop();
    }
    
    public int top() {
        return nmStack.peek();
    }
    
    public int min() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

从上到下打印二叉树②

剑指 Offer 32 - II. 从上到下打印二叉树 II

方法1:辅助队列

利用队列的先入先出的特点

这道题题干要求可以分析出:

1."同一层节点从左往右打印",代表每次都是左子树先入队列,右子树再入队列

2."每一层打印到一行",代表一行的节点要放到一个ArrayList中

3.每一层的ArrayList要放到大的ArrayList中,最终返回的是大的ArrayList

具体:

1.新建Integer类型的大ArrayList并判断边界:root是否为null

2.新建TreeNode类型的队列,并把root放到队列中

3.开始循环,循环条件是队列不为空.

3.1由于每层的节点打印到一行,因此要在循环中首先新建Integer类型的小ArrayList

3.2计算当前队列的长度,并且把这个作为循环条件

这一步很重要,因为包含在这个长度里的队列中的元素,一会儿会放到小ArrayList中,这个计算长度其实是在控制每层放进ArrayList中元素的数量,防止后面中加元素的时候会搞乱

3.2.1创建一个节点cur来接收que.poll()

这个cur也很重要,有了他,就可以把它放到ArrayList中(但是别忘了是cur.val而不是 cur),并且通过他,把左子树和右子树offer进队列了.不过offer的时候注意要有一个限制条件:如果左子树不为空,右子树不为空才offer,不然不offer

3.2.2别忘了,循环一次就要让当前队列长度-1

3.3把小ArrayList放到大ArrayList中

4.循环结束,返回大ArrayList
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res=new ArrayList<>();
        if(root==null){
            return res;
        }
        Queue<TreeNode> que=new LinkedList<>();
        que.offer(root);
        while(!que.isEmpty()){
            List<Integer> tmp=new ArrayList<>();
            int s=que.size();
            while(s!=0){
                TreeNode cur=que.poll();
                tmp.add(cur.val);
                if(cur.left!=null){
                    que.offer(cur.left);
                }
                if(cur.right!=null){
                    que.offer(cur.right);
                }
                s--;
            }
            res.add(tmp);
        }
        return res;
    }
}

数组中出现次数超过一半的数字

剑指 Offer 39. 数组中出现次数超过一半的数字

方法1:排序
class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[(nums.length-1)/2];
    }
}
方法2:哈希表（借鉴自官方官方解题思路）
class Solution {
    private Map<Integer, Integer> countNums(int[] nums) {
        Map<Integer, Integer> counts = new HashMap<Integer, Integer>();
        for (int num : nums) {
            if (!counts.containsKey(num)) {
                counts.put(num, 1);
            } else {
                counts.put(num, counts.get(num) + 1);
            }
        }
        return counts;
    }

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> counts = countNums(nums);

        Map.Entry<Integer, Integer> majorityEntry = null;
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
                majorityEntry = entry;
            }
        }

        return majorityEntry.getKey();
    }
}
方法3:摩尔投票法（借鉴自这位大佬大佬的解题思路）

核心理念为票数正负抵消。此方法时间和空间复杂度分别为O(N)和O(1) ，为本题的最佳解法

具体：

1.初始化：票数统计 votes = 0 ，众数 x；
2.循环：遍历数组 nums 中的每个数字 num ；
3.当票数 votes 等于 0 ，则假设当前数字 num 是众数；
4.当 num = x 时，票数 votes 自增 1 ；当 num != x 时，票数 votes 自减 1 ；
5.返回值：返回 x 即可
class Solution {
    public int majorityElement(int[] nums) {
        int votes=0;
        int zhong=0;
        for(int i=0;i<nums.length;i++){
            if(votes==0){
                zhong=nums[i];
                votes++;
            }
            else if(nums[i]==zhong){
                votes++;
            }
            else if(nums[i]!=zhong){
                votes--;
            }
        }
        return zhong;
    }
}

最小的k个数

剑指 Offer 40. 最小的k个数

方法1：优先级队列（TOPK问题）

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if(arr.length==0 || k==0)return new int[0];
        PriorityQueue<Integer> pq=new PriorityQueue<>((o1,o2)->o2-o1);
        for(int i=0;i<k;i++){
            pq.offer(arr[i]);
        }
        for(int i=k;i<arr.length;i++){
            if(pq.peek()>arr[i]){
                pq.poll();
                pq.offer(arr[i]);
            }
        }
        int[] res=new int[pq.size()];
        int index=0;
        while(pq.size()!=0){
            res[index++]=pq.poll();
        }
        return res;
    }
}

连续子数组的最大和

剑指 Offer 42. 连续子数组的最大和

方法1:动态规划

你需要知道为什么这道题会用动态规划来解决,动态规划的特点是什么

知道了这个,就能很轻松的想通该如何解了

新建的数组dp长度和nums一样,因为我们要实时记录当前子数组的和的最大值

具体怎么个操作法呢?

首先dp[0]中直接放nums[0]的值,因为这是当前子数组nums[0]的和的最大值就是它本身

接下来从1下标开始遍历,就需要两个数组"联动"了

这个联动你们自行体会下,根据动态规划的特点去体会吧~我尝试用文字描述但是有点费劲...
class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp=new int[nums.length];
        dp[0]=nums[0];
        for(int i=1;i<nums.length;i++){
            if(dp[i-1]<=0){
                dp[i]=nums[i];
            }
            else{
                dp[i]=dp[i-1]+nums[i];
            }
        }
        int result=dp[0];
        for(int i=1;i<dp.length;i++){
            if(dp[i]>result){
                result=dp[i];
            }
        }
        return result;
    }
}

第一个只出现一次的字符

剑指 Offer 50. 第一个只出现一次的字符

方法2比方法1更高效

方法1:哈希表

方法1需遍历 s 两轮

class Solution {
    public char firstUniqChar(String s) {
        HashMap<Character, Boolean> dic = new HashMap<>();
        char[] sc = s.toCharArray();
        for(char c : sc)
            dic.put(c, !dic.containsKey(c));
        for(char c : sc)
            if(dic.get(c)) return c;
        return ' ';
    }
}

方法2:有序哈希表(有序哈希表中的键值对是按照插入顺序排序的)

方法2遍历 s 一轮,遍历dic一轮

class Solution {
    public char firstUniqChar(String s) {
        Map<Character, Boolean> dic = new LinkedHashMap<>();
        char[] sc = s.toCharArray();
        for(char c : sc)
            dic.put(c, !dic.containsKey(c));
        for(Map.Entry<Character, Boolean> d : dic.entrySet()){
           if(d.getValue()) return d.getKey();
        }
        return ' ';
    }
}

两个链表的第一个公共节点

剑指 Offer 52. 两个链表的第一个公共节点

方法1:双指针

我个人认为是很巧妙的思路

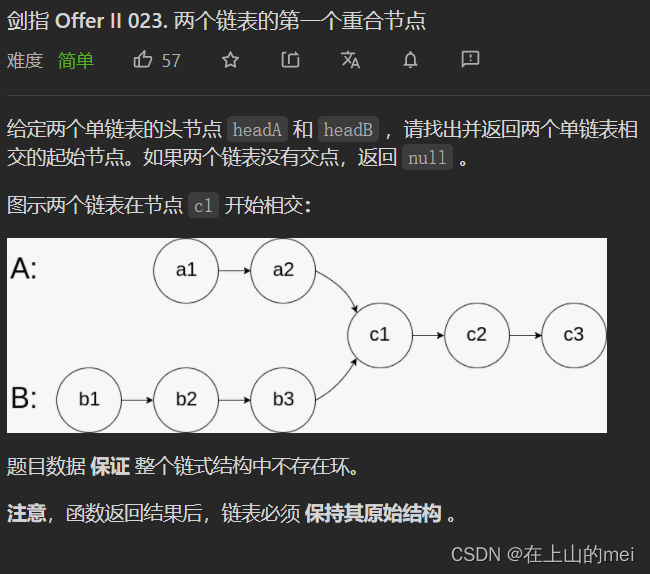
由于A、B两个链表A+B和B+A的是一样的，因此我们只需要创建两个指针hA和hB，分别从链表A的headA节点和链表B的headB节点出发，然后next到null就跳转到另一个链表，这样最终一定会在各自跳转到另一个链表中时遇到
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
class Solution {
    ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if(headA==null || headB==null){
            return null;
        }
        ListNode hA=headA;
        ListNode hB=headB;
        while(hA!=hB){
            hA=hA==null?headB:hA.next;
            hB=hB==null?headA:hB.next;
        }
        return hA;
    }
}

在排序数组中查找数字①

剑指 Offer 53 - I. 在排序数组中查找数字 I

方法1:二分法

排序数组中的搜索问题，首先想到二分法解决

具体:

1.初始化：左边界 i = 0，右边界 j = len(nums) - 1
2.循环二分：当闭区间 i>j时跳出
计算中点 m = (i + j) / 2（向下取整）；
(1)若 nums[m] < target，则 target在闭区间 [m + 1, j] 中，因此执行 i = m + 1；
(2) 若 nums[m] > target，则 target在闭区间 [i, m - 1]中，因此执行 j = m - 1；
(3)若 nums[m] = target，则右边界 right在闭区间 [m+1, j]中；左边界 left在闭区间 [i, m-1] 中。(我们求出的left和right分别是target左边一个和trget右边一个的位置)

细讲一下(3):如果我们按最基本的二分法去做的话,那么我们需要使用两次二分法,第一次用来求right,第二次用来求left.不过我们可以优化一下,让这两次二分不走的那么实诚.

什么意思?

优化下的二分法:

第一次循环完成跳出循环的时候,把i赋给right,然后这个时候我们判断下,j如果j

>=0 && nums[j]!=target说明数组中就没有target这个值,因此我们就可以直接返回0;如果这里判断完了发现数组中有target这个值,且nums[j]=target,那么我们在进行第二次二分法.不过第二次不用那么实诚,意思是i还是回到下标0,但是j就呆在原地就行了,不需要再回到nums.length-1,这样第二次二分法就能缩小寻找的区间了.然后通过第二次二分法找到left.

3.返回值：最终返回 right - left - 1即可。

参考:大佬思路
class Solution {
    public int search(int[] nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 left
        i = 0;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
}
方法2:哈希表
class Solution {
    public int search(int[] nums, int target) {
        if(nums.length==0){
            return 0;
        }
        Map<Integer,Integer> map=new HashMap<>();
        for(int n:nums){
            if(map.containsKey(n)){
                int val=map.get(n);
                map.put(n,val+1);
            }
            else{
                map.put(n,1);
            }
        }
        if(map.containsKey(target)){
            return map.get(target);
        }
        return 0;
    }
}

0~n-1中缺失的数字

剑指 Offer 53 - II. 0～n-1中缺失的数字

方法1:二分法

排序数组中的搜索问题,首先想到二分法解决

根据题意,数组可以分为两部分,左子数组和右子数组.左子数组:nums[i]=i,右子数组nums[i]!=i

我们要找的就是右子数组的首位元素的下标

具体:

1.初始化:左边界i=0,右边界j=nums.length-1

2.循环二分:当i<=j时循环

2.1计算重点下标m

2.2让nums[m]和m作比较

(1)若nums[m]==m,则右子数组的首位元素一定在[m+1,j]中,因此让i=m+1

(2)若nums[m]!=m,则左子数组的末尾元素一定在[i,m-1]中,因此j=m-1

3.返回值:返回i
class Solution {
    public int missingNumber(int[] nums) {
        int i=0;
        int j=nums.length-1;
        while(i<=j){
            int m=(i+j)/2;
            if(nums[m]==m){
                i=m+1;
            }
            else{
                j=m-1;
            }
        }
        return i;
    }
}

二叉搜索树的第k大节点

剑指 Offer 54. 二叉搜索树的第k大节点

方法1:中序遍历的倒序+提前返回

根据二叉搜索树基本性质:根节点的左子树的值都比它小,根节点的右子树的值都比它大

可以得出,二叉搜索树的中序遍历为递增序列

那么进而能推出,二叉搜索树的中序遍历的倒序为递减序列

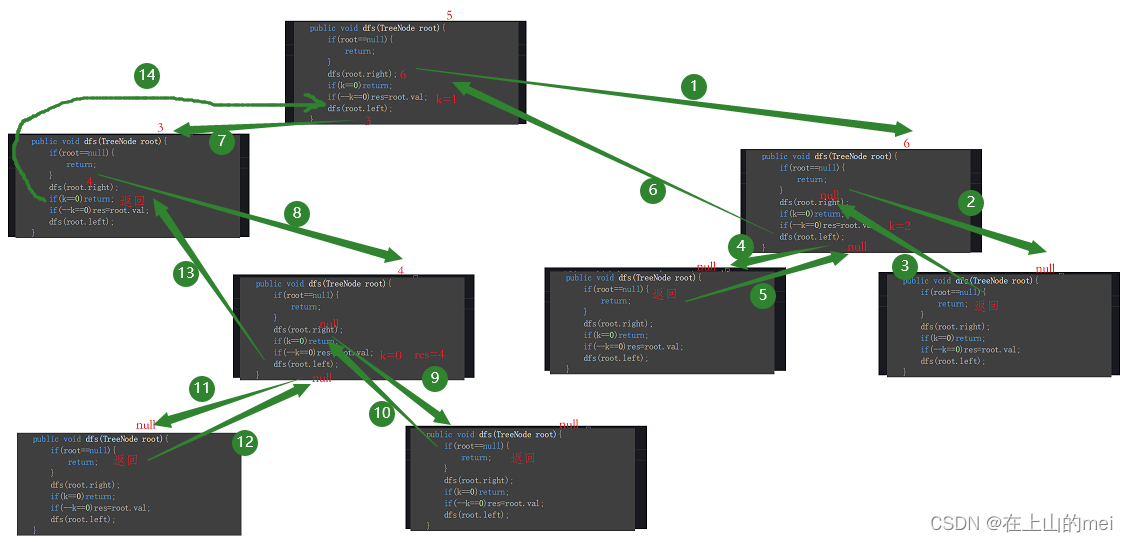
那么我们这道题就相当于是求这个二叉搜索树的中序遍历的倒序的第k个节点

具体:

1.终止条件:root==null

2.递归右子树

3.(1)如果k==0,代表已经找到目标节点,那么就可以直接返回

(2)不满足(1),那么k=k-1

(3)如果k==0,代表当前节点为要找的节点,res=root.val

4.递归左子树
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int res,k;
    public int kthLargest(TreeNode root, int k) {
        this.k=k;
        dfs(root);
        return res;

    }
    public void dfs(TreeNode root){
        if(root==null){
            return;
        }
        dfs(root.right);
        if(k==0)return;
        if(--k==0)res=root.val;
        dfs(root.left);
    }
}

二叉树的深度

剑指 Offer 55 - I. 二叉树的深度

方法1:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){
            return 0;
        }
        int leftT=maxDepth(root.left);
        int rightT=maxDepth(root.right);
        return leftT>=rightT?leftT+1:rightT+1;
    }
}

平衡二叉树

剑指 Offer 55 - II. 平衡二叉树

方法1:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null)return true;
        if(isBalanced2(root)==-1)return false;
        return true;
    }
    public int isBalanced2(TreeNode root){
        if(root==null)return 0;
        int leftT=isBalanced2(root.left);
        if(leftT==-1){
            return -1;
        }
        int rightT=isBalanced2(root.right);
        if(rightT==-1){
            return -1;
        }
        return Math.abs(leftT-rightT)<=1?Math.max(leftT,rightT)+1:-1;
    }
}

和为s的两个数字

剑指 Offer 57. 和为s的两个数字

排序数组中的搜索问题,首先想到二分法解决

方法1:二分法

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int i=0;
        int j=nums.length-1;
        while(i<j){
            if((nums[i]+nums[j])<target){
                i++;
            }
            else if((nums[i]+nums[j]>target)){
                j--;
            }
            else{
                break;
            }
        }
        return new int[]{nums[i],nums[j]};
    }
}

和为s的连续正数序列

剑指 Offer 57 - II. 和为s的连续正数序列

方法1:滑动窗口(借鉴大佬1的做法:大佬做法)

方法1设滑动窗口是"左闭右开"区间,因为题目说至少含有两个数,说明滑动窗口至少包含两个数,因此创建i=1,j=3,这样一来,初始s=3(滑动窗口内元素之和)

循环条件是i<=target/2是因为,也是因为题目说至少含有两个数,因此如果i对应的元素已经大于target,那么后面的数就只能比i大,因此就一定不符合滑动窗口中的元等于target,因此跳出循环
public int[][] findContinuousSequence(int target) {
    int i = 1; // 滑动窗口的左边界
    int j = 3; // 滑动窗口的右边界
    int sum = 3; // 滑动窗口中数字的和
    List<int[]> res = new ArrayList<>();

    while (i <= target / 2) {
        if (sum < target) {
            // 右边界向右移动
            sum += j;
            j++;
        } else if (sum > target) {
            // 左边界向右移动
            sum -= i;
            i++;
        } else {
            // 记录结果
            int[] arr = new int[j-i];
            for (int k = i; k < j; k++) {
                arr[k-i] = k;
            }
            res.add(arr);
            // 左边界向右移动
            sum -= i;
            i++;
        }
    }

    return res.toArray(new int[res.size()][]);
}
方法2:滑动窗口(借鉴大佬2的做法:大佬做法)

方法2设滑动窗口是"左闭右闭"区间,因为题目说至少含有两个数,说明滑动窗口至少包含两个数,因此创建i=1,j=2,这样一来,初始s=3(滑动窗口内元素之和)
class Solution {
    public int[][] findContinuousSequence(int target) {
        int i=1,j=2,s=3;
        List<int[]> tmp=new ArrayList<>();
        while(i<j){
            if(s==target){
                int[] arr=new int[j-i+1];
                for(int k=i;k<=j;k++){
                    arr[k-i]=k;
                }
                tmp.add(arr);
            }
            if(s>=target){
                s-=i;
                i++;
            }
            else{
                j++;
                s+=j;
            }
        }
        int[][] res=new int[0][tmp.size()];
        return tmp.toArray(res);
    }
}

翻转单词顺序

剑指 Offer 58 - I. 翻转单词顺序

方法1:双指针

class Solution {
    public String reverseWords(String s) {
        if(s.length()==0)return "";
        s.trim();
        // char[] ch=s.toCharArray();
        int i=s.length()-1;
        int j=s.length()-1;
        StringBuilder str=new StringBuilder();
        while(i>=0 && j>=0){
            while(i>=0 && s.charAt(i)!=' '){
                i--;
            }
            str.append(s.substring(i+1,j+1)+" ");
            while(i>=0 && s.charAt(i)==' '){
                i--;
            }
            j=i;
        }
        return str.toString().trim();
    }
}

方法2:分割+倒序

上面这个图是复制的大佬的图

class Solution {
    public String reverseWords(String s) {
        String[] strs = s.trim().split(" "); 
        StringBuilder res = new StringBuilder();
        for(int i = strs.length - 1; i >= 0; i--) { 
            if(strs[i].equals("")) continue; 
            res.append(strs[i] + " ");
        }
        return res.toString().trim(); 
    }
}

左旋转字符串

剑指 Offer 58 - II. 左旋转字符串

方法1:使用StringBuilder拼接

class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder res = new StringBuilder();
        for(int i = n; i < s.length(); i++)
            res.append(s.charAt(i));
        for(int i = 0; i < n; i++)
            res.append(s.charAt(i));
        return res.toString();
    }
}

简化:

class Solution {
    public String reverseLeftWords(String s, int n) {
        StringBuilder res = new StringBuilder();
        for(int i = n; i < n + s.length(); i++)
            res.append(s.charAt(i % s.length()));
        return res.toString();
    }
}

方法2:使用String+号拼接

class Solution {
    public String reverseLeftWords(String s, int n) {
        String res = "";
        for(int i = n; i < s.length(); i++)
            res += s.charAt(i);
        for(int i = 0; i < n; i++)
            res += s.charAt(i);
        return res;
    }
}

简化:

class Solution {
    public String reverseLeftWords(String s, int n) {
        String res = "";
        for(int i = n; i < n + s.length(); i++)
            res += s.charAt(i % s.length());
        return res;
    }
}

方法3:切片

class Solution {
    public String reverseLeftWords(String s, int n) {
        return s.substring(n, s.length()) + s.substring(0, n);
    }
}

圆圈中最后剩下的数字

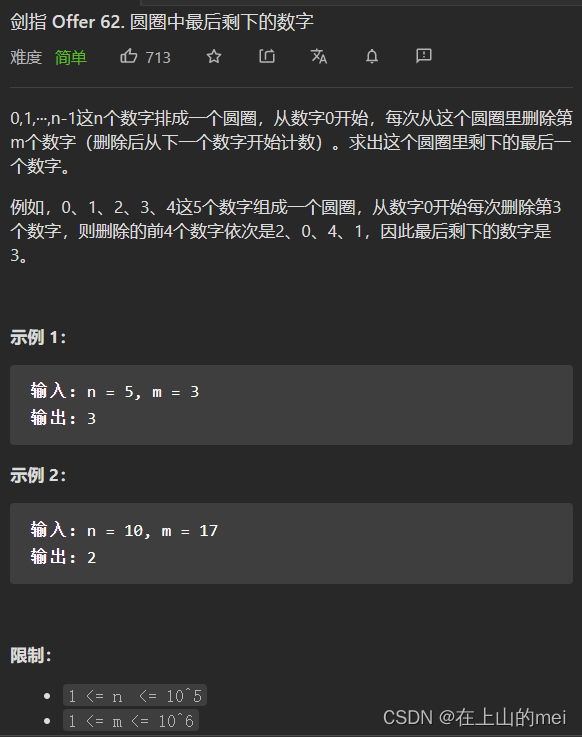
剑指 Offer 62. 圆圈中最后剩下的数字

方法1:模拟链表(基于ArrayList)

这种方法可以勉强通过,时间复杂度是o(n^2),但是显然是不太好的方法

参考大佬:大佬做法
class Solution {
    public int lastRemaining(int n, int m) {
        List<Integer> list=new ArrayList<>();
        for(int i=0;i<n;i++){
            list.add(i);
        }
        int idx=0;
        while(n>1){
            idx=(idx+m-1)%n;
            n--;
            list.remove(idx);
        }
        return list.get(0);
    }
}
方法2:数学解法(妙啊妙啊~)

参考大佬:大佬做法
class Solution {
    public int lastRemaining(int n, int m) {
        int idx=0;
        for(int i=2;i<=n;i++){
            idx=(idx+m)%i;
        }
        return idx;
    }
}

不用加减乘除做加法

剑指 Offer 65. 不用加减乘除做加法

方法1:位运算

参考大佬:大佬做法
class Solution {
    public int add(int a, int b) {
        while(b!=0){
            int c=(a&b)<<1;
            a=a^b;
            b=c;
        }
        return a;
    }
}

二叉搜索树的最近公共祖先

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

参考大佬:大佬思路

方法1:迭代

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(p.val>q.val){
            TreeNode tmp=p;
            p=q;
            q=tmp;
        }
        while(root!=null){
            if(root.val<p.val){
                root=root.right;
            }
            else if(root.val>q.val){
                root=root.left;
            }
            else{
                break;
            }
        }
        return root;
    }
}

方法2:递归

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root.val < p.val && root.val < q.val)
            return lowestCommonAncestor(root.right, p, q);
        if(root.val > p.val && root.val > q.val)
            return lowestCommonAncestor(root.left, p, q);
        return root;
    }
}

二叉树的最近公共祖先

剑指 Offer 68 - II. 二叉树的最近公共祖先

方法1:递归

参考大佬:大佬思路

二叉树的最近公共祖先要比二叉搜索树的难一点,不过能难倒咱吗,不能!不会就多看几遍,画图.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null || root.val==p.val || root.val==q.val)return root;
        TreeNode left=lowestCommonAncestor(root.left,p,q);
        TreeNode right=lowestCommonAncestor(root.right,p,q);
        if(left==null && right==null)return null;
        if(left==null)return right;
        if(right==null)return left;
        return root;
    }
}

整数除法

剑指 Offer II 001. 整数除法

思路思路思路

说实话这题还得再看

class Solution {

    public int divide(int a, int b) {
        int flag = 0;
        if (a > 0) {
            a = -a;
            flag += 1;
        }

        if (b > 0) {
            b = -b;
            flag += 1;
        }
        int ret = calc(a, b);
        if (flag != 1 && ret == Integer.MIN_VALUE) {
            ret++;
        }
        return flag == 1 ? ret : -ret;
    }

    private int calc(int a, int b) {
        int ret = 0;
        while (a <= b) {
            int cnt = 1;
            int val = b;
            while (val >= Integer.MIN_VALUE >> 1  && a <= val << 1) {
                cnt += cnt;
                val += val;
            }
            ret -= cnt;
            a -= val;
        }
        return ret;
    }
}

二进制加法

剑指 Offer II 002. 二进制加法

class Solution {
    public String addBinary(String a, String b) {
        StringBuilder str=new StringBuilder();
        int i=a.length()-1;
        int j=b.length()-1;
        int jinwei=0;
        while(i>=0 || j>=0 || jinwei!=0){
            int nowa=i>=0?a.charAt(i)-'0':0;
            int nowb=j>=0?b.charAt(j)-'0':0;
            int sum=nowa+nowb+jinwei;
            jinwei=sum>=2?1:0;
            sum=sum>=2?sum-2:sum;
            str.append(sum);
            i--;
            j--;
        }
        return str.reverse().toString();
    }
}

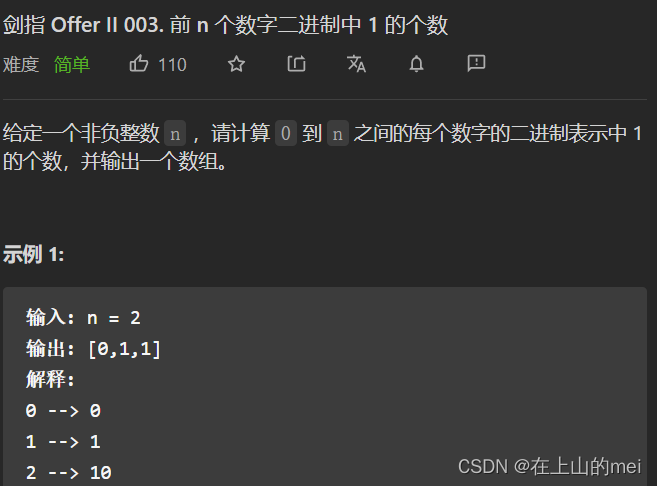
前n个数字二进制中1的个数

剑指 Offer II 003. 前 n 个数字二进制中 1 的个数

方法1:动态规划+位运算

大佬思路
class Solution {
    public int[] countBits(int n) {
        int[] dp=new int[n+1];
        dp[0]=0;
        for(int i=1;i<dp.length;i++){
            dp[i]=dp[i>>1]+(i&1);
        }
        return dp;
    }
}

排序数组中两个数字之和

剑指 Offer II 006. 排序数组中两个数字之和

方法1:二分法

思路

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        for (int i = 0; i < numbers.length; ++i) {
            int low = i + 1, high = numbers.length - 1;
            while (low <= high) {
                int mid = (high - low) / 2 + low;
                if (numbers[mid] == target - numbers[i]) {
                    return new int[]{i, mid};
                } else if (numbers[mid] > target - numbers[i]) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            }
        }
        return new int[]{-1, -1};
    }
}

方法二:双指针

思路

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int left=0;
        int right=numbers.length-1;
        while(left<right){
            int sum=numbers[left]+numbers[right];
            if(sum>target){
                right--;
            }
            else if(sum<target){
                left++;
            }
            else{
                break;
            }
        }
        return new int[]{left,right};
    }
}

左右两边子数组的和相等

剑指 Offer II 012. 左右两边子数组的和相等

方法1:前缀和

思路
class Solution {
    public int pivotIndex(int[] nums) {
        int sum=0;
        for(int num:nums)sum+=num;
        int leftsum=0;
        for(int i=0;i<nums.length;i++){
            if(leftsum*2+nums[i]==sum){
                return i;
            }
            leftsum+=nums[i];
        }
        return -1;
    }
}
下面这个也是利用了前缀和这个方法,但是和上面的代码不同的是在求nums数组中元素相加之和的时候用的是API函数,下面这段代码的执行时间比上面代码慢,但是这种利用API函数求和的代码更简单,鉴于知道这种思路,因此我把他也放在这里供参考 JDK1.8 Arrays.Stream()用法和介绍_互联网底层人员的博客-优快云博客_arrays.stream()
class Solution {
    public int pivotIndex(int[] nums) {
        int sum=Arrays.stream(nums).sum();
        int leftsum=0;
        for(int i=0;i<nums.length;i++){
            if(leftsum*2+nums[i]==sum){
                return i;
            }
            leftsum+=nums[i];
        }
        return -1;
    }
}

有效的回文

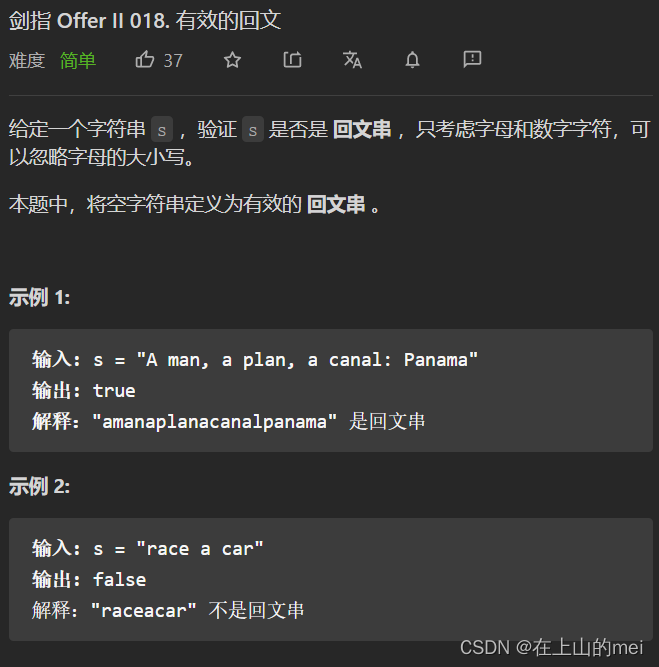
剑指 Offer II 018. 有效的回文

方法1:双指针+借助库函数

思路

java.lang.Character.isLetterOrDigit()方法实例 -java.lang

class Solution {
    public boolean isPalindrome(String s) {
        int n = s.length();
        int left = 0, right = n - 1;
        while (left < right) {
            while (left < right && !Character.isLetterOrDigit(s.charAt(left))) {
                ++left;
            }
            while (left < right && !Character.isLetterOrDigit(s.charAt(right))) {
                --right;
            }
            if (left < right) {
                if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) {
                    return false;
                }
                ++left;
                --right;
            }
        }
        return true;
    }
}

方法2:双指针+不借助库函数

class Solution {
    public boolean isPalindrome(String s) {
        int l = 0, r = s.length() - 1;
        char[] arr = s.toCharArray();
        while(l < r){
            while(l < r && !isValid(arr[l])) l++;
            while(l < r && !isValid(arr[r])) r--;
            if(arr[l] != arr[r] && arr[l] != (arr[r] ^ 32)){
                return false;
            }
            l++;
            r--;
        }
        return true;
    }
    private boolean isValid(char x){
        int val = x - '0';
        if(val <= 9 && val >= 0) return true; // 是数字
        val = x - 'a';
        if(val <= 25 && val >= 0) return true; // 是小写字母
        val = x - 'A';
        if(val <= 25 && val >= 0) return true; // 是大写字母
        return false;
    }
}

最多删除一个字符得到回文

剑指 Offer II 019. 最多删除一个字符得到回文

方法1:双指针,通过贪心算法实现

思路

class Solution {
    public boolean validPalindrome(String s) {
        int low = 0, high = s.length() - 1;
        while (low < high) {
            char c1 = s.charAt(low), c2 = s.charAt(high);
            if (c1 == c2) {
                ++low;
                --high;
            } else {
                return validPalindrome(s, low, high - 1) || validPalindrome(s, low + 1, high);
            }
        }
        return true;
    }

    public boolean validPalindrome(String s, int low, int high) {
        for (int i = low, j = high; i < j; ++i, --j) {
            char c1 = s.charAt(i), c2 = s.charAt(j);
            if (c1 != c2) {
                return false;
            }
        }
        return true;
    }
}

两个链表的第一个重合节点

剑指 Offer II 023. 两个链表的第一个重合节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if(headA==null || headB==null)return null;
        ListNode curA=headA;
        ListNode curB=headB;
        while(curA!=curB){
            curA=curA==null?headB:curA.next;
            curB=curB==null?headA:curB.next;
        }
        return curA;
    }
}

翻转链表

剑指 Offer II 024. 反转链表

方法1:不带傀儡节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null)return null;
        ListNode cur=head;
        ListNode curN=cur.next;
        while(curN!=null){
            ListNode curNN=curN.next;
            curN.next=cur;
            cur=curN;
            curN=curNN;
        }
        //记得最后head指向空
        head.next=null;
        return cur;
    }
}

方法2:带傀儡节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if(head==null)return null;
        ListNode pre=null;
        ListNode cur=head;
        while(cur!=null){
            ListNode curN=cur.next;
            cur.next=pre;
            pre=cur;
            cur=curN;
        }
        return pre;
    }
}

回文链表

剑指 Offer II 027. 回文链表

方法1:快慢指针

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode pre=new ListNode(-1);
        pre.next=head;
        ListNode fast=pre;
        ListNode slow=pre;
        while(fast!=null && fast.next!=null){
            fast=fast.next.next;
            slow=slow.next;
        }
        slow=slow.next;
        slow=reverseL(slow);
        fast=head;
        while(slow!=null){
            if(fast.val!=slow.val)return false;
            fast=fast.next;
            slow=slow.next;
        }
        return true;
    }
    public ListNode reverseL(ListNode head){
        ListNode pre=null;
        ListNode cur=head;
        while(cur!=null){
            ListNode curN=cur.next;
            cur.next=pre;
            pre=cur;
            cur=curN;
        }
        return pre;
    }
}

有效的变位词

剑指 Offer II 032. 有效的变位词

方法1:排序

class Solution {
    public boolean isAnagram(String s, String t) {
        if(s.equals(t) || s.length()!=t.length())return false;
        char[] ss=s.toCharArray();
        Arrays.sort(ss);
        char[] tt=t.toCharArray();
        Arrays.sort(tt);
        for(int i=0;i<ss.length;i++){
            if(ss[i]!=tt[i])return false;
        }
        return true;

    }
}

方法2:数组

class Solution {
    public boolean isAnagram(String s, String t) {
        int ns = s.length(), nt = t.length();
        if(s.equals(t) || ns != nt) return false; // 特判
        int[] counts = new int[26];
        for(int i = 0; i < ns; i++){
            counts[s.charAt(i) - 'a']++; // 累计
            counts[t.charAt(i) - 'a']--; // 抵消
        }
        for(int count : counts){
            if(count != 0) return false;
        }
        return true;
    }
}

外星语言是否排序

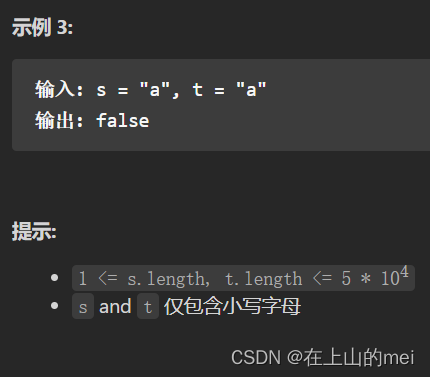
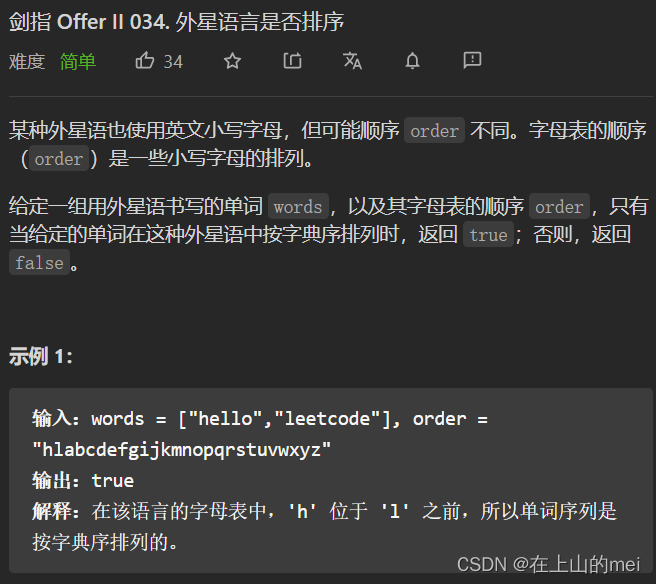
剑指 Offer II 034. 外星语言是否排序

方法1:数组

具体:外星语字母表顺序虽然跟我们平常的字母表不一样且只有小写字母,但是总归不还是那26个字母吗.所以我们可以创建一个长度为26的数组arr,然后遍历字符串order,通过order.charAt(i)-'a'的方式相当于给外星语每个字母标序.

之后就是开始比较words数组中的单词了,两两比较.

因为我设定的是words[i]和words[i+1]比较,因此注意边界是words.length-1.

确定了要比较的两个单词以后,就要开始比较两个单词中的每个字母的顺序了.(这里的思路我就省了,看代码+用示例试一下应该就能懂了,用文字解释有点难所以就不解释了)
class Solution {
    public boolean isAlienSorted(String[] words, String order) {
        int[] arr=new int[26];
        for(int i=0;i<arr.length;i++){
            arr[order.charAt(i)-'a']=i;
        }
        for(int i=0;i<words.length-1;i++){
            String w1=words[i];
            String w2=words[i+1];
            for(int j=0;j<Math.max(w1.length(),w2.length());j++){
                int ww1=j>=w1.length()?-1:arr[w1.charAt(j)-'a'];
                int ww2=j>=w2.length()?-1:arr[w2.charAt(j)-'a'];
                if(ww1<ww2){
                    break;
                }
                if(ww1>ww2){
                    return false;
                }
            }
        }
        return true;
    }
}

滑动窗口的平均值

剑指 Offer II 041. 滑动窗口的平均值

方法1:双端队列

思路

class MovingAverage {
    Deque<Integer> de;
    int size;
    int sum;
    /** Initialize your data structure here. */
    public MovingAverage(int size) {
        de=new LinkedList<>();
        this.size=size;
    }
    
    public double next(int val) {
        if(de.size()<size){
            de.offerLast(val);
            sum+=val;
        }
        else{
            sum-=de.peekFirst();
            de.removeFirst();
            de.offerLast(val);
            sum+=val;

        }
        return sum*1.0/de.size();
    }
}

/**
 * Your MovingAverage object will be instantiated and called as such:
 * MovingAverage obj = new MovingAverage(size);
 * double param_1 = obj.next(val);
 */

方法2:双指针

思路

class MovingAverage {

    List<Integer> data;
    int size;
    int leftIndex;
    int rightIndex;
    double sum;

    /**
     * Initialize your data structure here.
     */
    public MovingAverage(int size) {
        data = new ArrayList<>();
        this.size = size;
        this.leftIndex = 0;
        this.rightIndex = 0;
        this.sum = 0;
    }

    public double next(int val) {
        data.add(val);
        sum += val;
        rightIndex++;
        //超范围,右移
        if (rightIndex - leftIndex > size) {
            sum = sum - data.get(leftIndex);
            leftIndex++;
        }
        return sum / (Math.min(data.size(), size));
    }
}

展平二叉搜索树

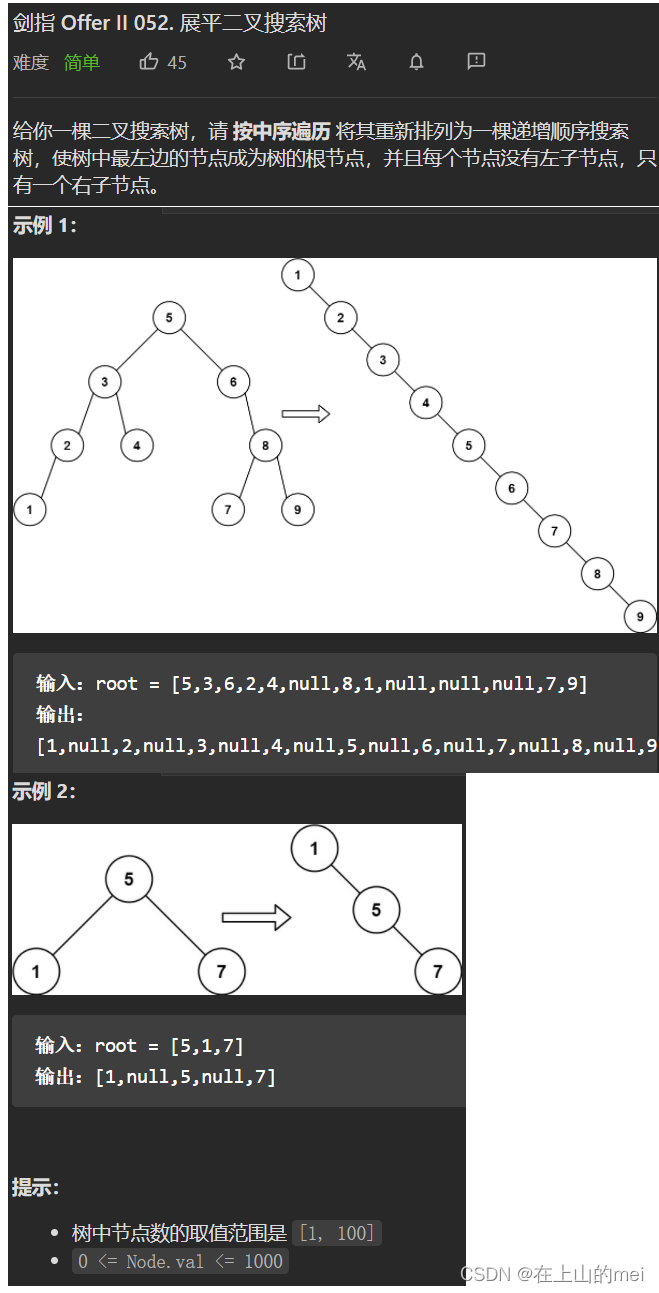
剑指 Offer II 052. 展平二叉搜索树

方法1：中序遍历后创建一个新的树（我是用队列实现的）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Deque<TreeNode> de=new LinkedList<>();
    public TreeNode increasingBST(TreeNode root) {
        inorder(root);
        TreeNode newroot=new TreeNode(-1);
        TreeNode cur=newroot;
        while(de.size()!=0){
            cur.right=new TreeNode(de.removeFirst().val);
            cur=cur.right;
        }
        return newroot.right;
    }

    public void inorder(TreeNode root){
        if(root==null)return;
        inorder(root.left);
        de.offerLast(root);
        inorder(root.right);
    }
    // public TreeNode danfenzhi(){
    //     if(de.size()==0)return 
    // }
}

方法2：中序遍历的过程中改变节点指向（在原来的树上做改动，不需要生成新的树）

思路

class Solution {
    private TreeNode resNode;

    public TreeNode increasingBST(TreeNode root) {
        TreeNode dummyNode = new TreeNode(-1);
        resNode = dummyNode;
        inorder(root);
        return dummyNode.right;
    }

    public void inorder(TreeNode node) {
        if (node == null) {
            return;
        }
        inorder(node.left);

        // 在中序遍历的过程中修改节点指向
        resNode.right = node;
        node.left = null;
        resNode = node;

        inorder(node.right);
    }
}

二叉搜索树中两个节点之和

剑指 Offer II 056. 二叉搜索树中两个节点之和

方法1：哈希表+深度优先

class Solution {
    Set<Integer> set = new HashSet<Integer>();

    public boolean findTarget(TreeNode root, int k) {
        if (root == null) {
            return false;
        }
        if (set.contains(k - root.val)) {
            return true;
        }
        set.add(root.val);
        return findTarget(root.left, k) || findTarget(root.right, k);
    }
}

数据流的第K大数值

剑指 Offer II 059. 数据流的第 K 大数值

方法1：优先级队列（TOPK问题）

class KthLargest {
    PriorityQueue<Integer> pq=new PriorityQueue<>();
    int k;
    public KthLargest(int k, int[] nums) {
        this.k=k;
        for(int i=0;i<nums.length;i++){
            if(i<k){
                pq.offer(nums[i]);
            }
            else{
                if(pq.peek()<nums[i]){
                    pq.poll();
                    pq.offer(nums[i]);
                }
            }
        }

    }
    
    public int add(int val) {
        if(pq.size()<k){
            pq.offer(val);
        }
        else{
            if(pq.size()>=k && pq.peek()<val){
                pq.poll();
                pq.offer(val);
            }
        }
        return pq.peek();
    }
}

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest obj = new KthLargest(k, nums);
 * int param_1 = obj.add(val);
 */

查找插入位置

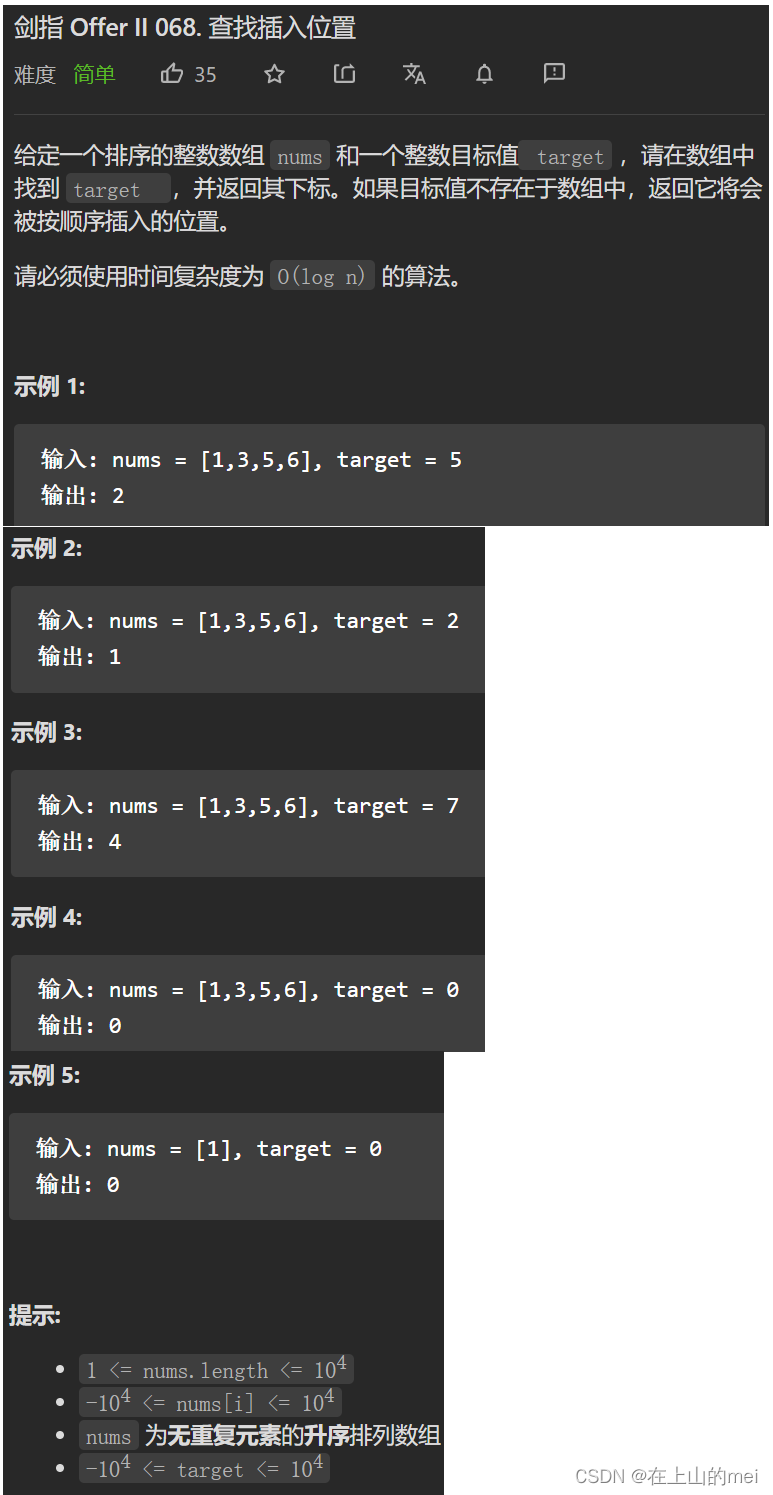
剑指 Offer II 068. 查找插入位置

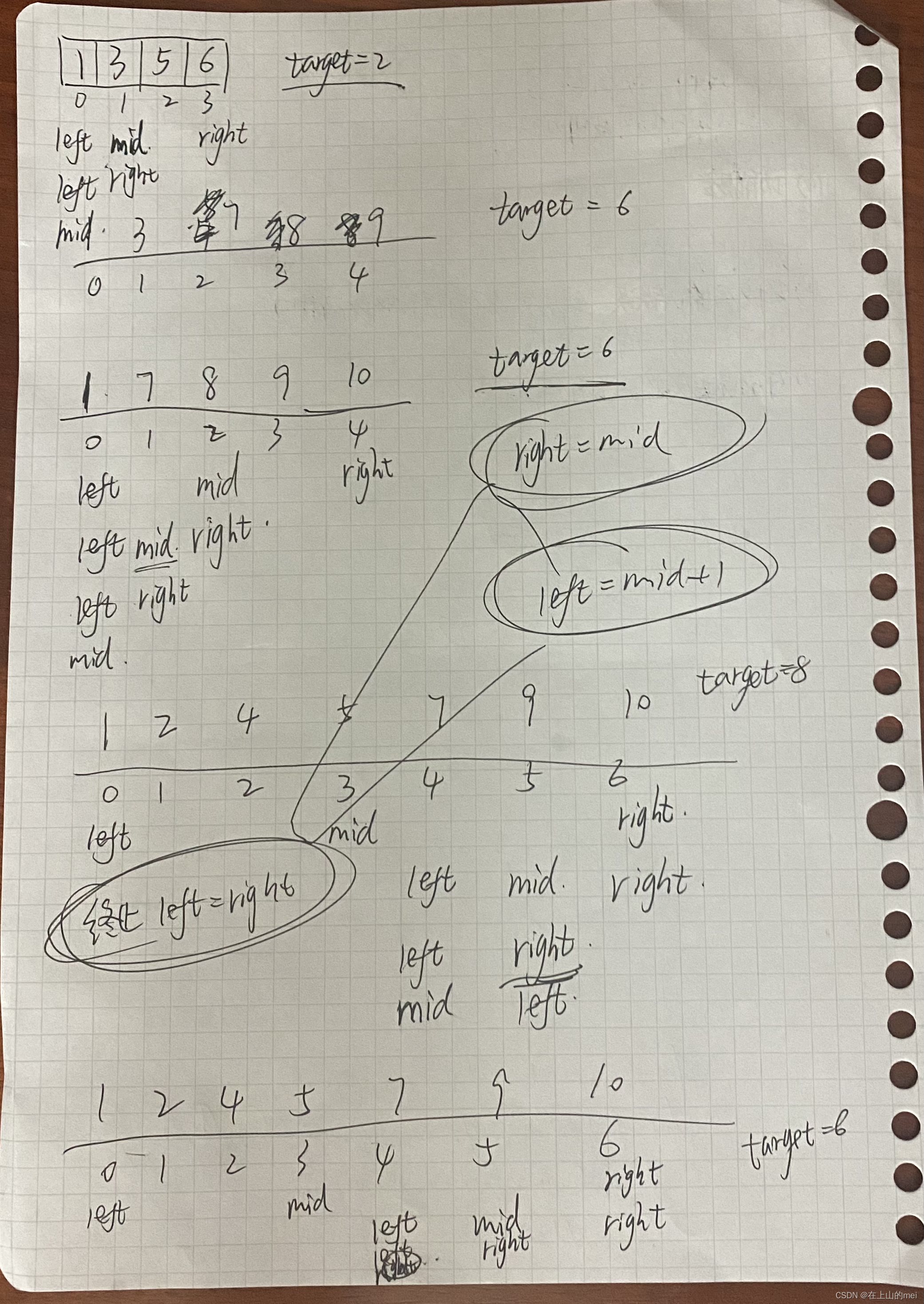
方法1：二分法

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left=0;
        int right=nums.length-1;
        if(nums[right]<target){
            return right+1;
        }
        while(left<right){
            int mid=(left+right)/2;
            if(nums[mid]>target){
                right=mid;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                right=mid;
                break;
            }
        }
        return right;
    }
}

山峰数组的顶部

剑指 Offer II 069. 山峰数组的顶部

方法1：枚举

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int cur=arr[0];
        for(int i=1;i<arr.length;i++){
            if(Math.max(cur,arr[i])==cur){
                cur=i-1;
                break;
            }
            else{
                cur=arr[i];
            }
        }
        return cur;
    }
}

方法2：二分法

思路

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int n = arr.length;
        int left = 1, right = n - 2, ans = 0;
        while (left <= right) {
            int mid = (left + right) / 2;
            if (arr[mid] > arr[mid + 1]) {
                ans = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }
}

求平方根

剑指 Offer II 072. 求平方根

方法1：二分法

思路

class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

数组相对排序

剑指 Offer II 075. 数组相对排序

方法1：计数排序

思路

class Solution {
    public int[] relativeSortArray(int[] arr1, int[] arr2) {
        int[] hash=new int[1001];
        for(int n:arr1){
            hash[n]++;
        }
        int index=0;
        for(int n:arr2){
            while(hash[n]-->0){
                arr1[index++]=n;
            }
        }
        for(int n=0;n<hash.length;n++){
            while(hash[n]-->0){
                arr1[index++]=n;
            }
        }
        return arr1;
    }
}

爬楼梯的最少成本

剑指 Offer II 088. 爬楼梯的最少成本

方法1：动态规划

思路

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len=cost.length;
        int[] dp=new int[len+1];
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<dp.length;i++){
            dp[i]=Math.min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]);
        }
        return dp[len];
    }
}

优化上面代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len=cost.length;
        int prev=0;
        int cur=0;
        for(int i=2;i<=len;i++){
            int next=Math.min(prev+cost[i-2],cur+cost[i-1]);
            prev=cur;
            cur=next;
        }   
        return cur;     
    }
}

分割等和子集

剑指 Offer II 101. 分割等和子集

这道题是背包问题，虽然有代码，但是我还不是很懂，还需要再看

方法1：动态规划

参考1

参考2

参考3（参考了评论区的两个代码）

二维数组：

class Solution {
    public boolean canPartition(int[] nums) {
        if(nums.length==1)return false;
        int mid = 0;
        int maxNum=0;
        for (int num : nums) {
            maxNum=Math.max(maxNum,num);
            mid += num;
        }
        if(maxNum>mid)return false;
        if (mid % 2 != 0) return false;
        mid >>= 1;

        boolean[][] dp = new boolean[nums.length + 1][mid + 1];
        dp[0][0] = true;
        for (int i = 1; i <= nums.length; i++) {
            for (int j = 0; j <= mid; j++) {
                // 不选中第i个的情况
                dp[i][j] = dp[i - 1][j];
                // 选中第i个的情况
                if (!dp[i][j] && j >= nums[i - 1]) {
                    dp[i][j] = dp[i - 1][j - nums[i - 1]];
                }
            }
        }
        return dp[nums.length][mid];
    }
}

一维数组：

class Solution {
    public boolean canPartition(int[] nums) {
        int target=0;//targrt初值
        for(int i:nums)target+=i;
        if(target%2==0)target>>=1;
        else return false;
        int len=nums.length;
        boolean[] dp=new boolean[target+1];
        dp[0]=true;
        for(int i=0;i<len;i++)
            for(int j=target;j>=nums[i];j--)
                dp[j]=dp[j] || dp[j-nums[i]];
        return dp[target];
    }
}

扑克牌中的顺子

面试题61. 扑克牌中的顺子

方法1：HashSet

class Solution {
    public boolean isStraight(int[] nums) {
        Set<Integer> set=new HashSet<>();
        int max=0;
        int min=14;
        for(int i=0;i<5;i++){
            if(nums[i]==0){
                continue;
            }
            max=Math.max(nums[i],max);
            min=Math.min(nums[i],min);
            if(set.contains(nums[i])){
                return false;
            }
            set.add(nums[i]);
        }
        if(max-min<5){
            return true;
        }
        return false;
    }
}