RC滤波电路

RC滤波电路

综述：本文简单讲述了RC低通滤波电路和RC高通滤波电路。

滤波电路是指过滤输入信号中不需要的信号，保留需要的信号。

一、RC低通滤波电路

1.定义：RC低通滤波电路：保留低频信号，衰减高频信号。

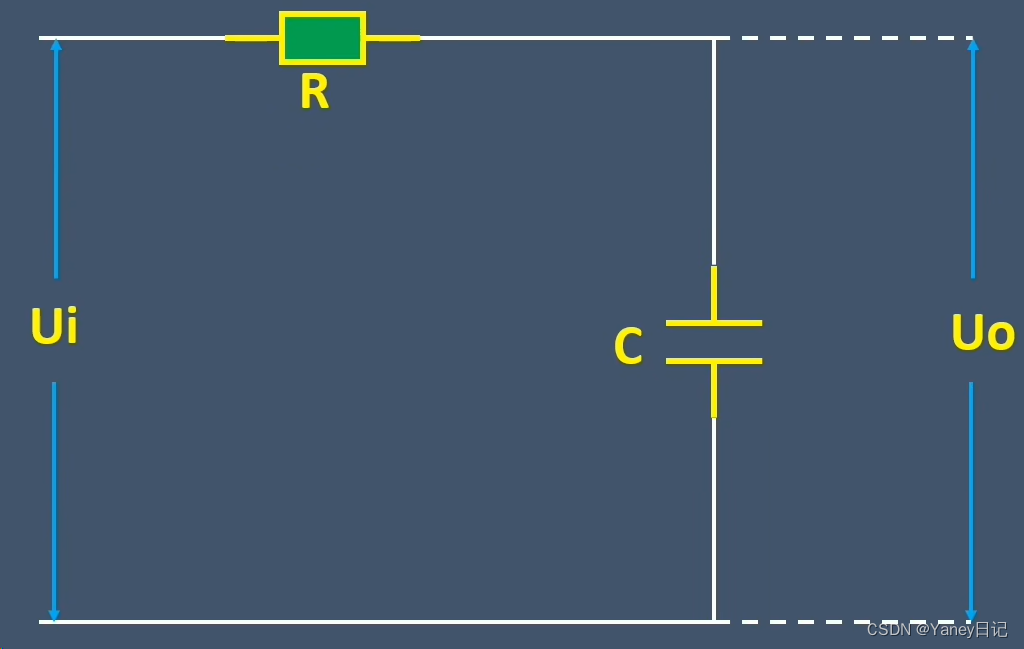
2.截止频率：信号衰减为原来0.7倍的信号频率，也即是衰减3db的信号频率，f=1/（2ΠRC）。小于截止频率时，信号基本不会衰减（衰减很小），大于截止频率时，信号每增长10倍，衰减也增长10倍，也即是-20db/十倍频。

3.计算：当需要设计一个截止频率为21KHz的RC低通滤波电路。由f=1/（2ΠRC）可知，f=21KHz，设C=10nf，可以得到R=750Ω。（RC低通滤波的电阻不能选太大，一般C为nf级，R为几百欧）

二、RC高通滤波电路

（同理，由RC低通滤波电路可以推出高通滤波电路的电路图和相应的特性。）

1.定义：RC低通滤波电路：保留高频信号，衰减低频信号（不导通直流信号）。

2.截止频率：信号衰减为原来0.7倍的信号频率，也即是衰减3db的信号频率，f=1/（2ΠRC）。大于截止频率时，信号基本不会衰减（衰减很小），小于截止频率时，信号每减少10倍，衰减也增长10倍，也即是-20db/十倍频。

---

学习视频：什么是RC低通滤波电路_哔哩哔哩_bilibili

侵权联系删除！