文章详细介绍了使用Verilog语言设计和仿真各种逻辑电路的过程，包括简单的连接、接地、或非、与非、异或等基本逻辑门，以及更复杂的组合逻辑电路。通过分析题目要求，使用assign语句和逻辑运算符构建电路模型，并通过仿真图验证设计的正确性。
文章目录
Exams/m2014 q4h
一、题目要求
创建一个具有一个输入和一个输出的模块，其行为类似于连接。
二、分析
连接输入输出，使用assign语句即可。这里要注意in和out是“有方向”的，你需要把in的值赋给out，而不能反过来，不然会报错。代码如下
module top_module( input in, output out );
assign out=in;
endmodule
三、仿真图
出现下图表示仿真成功
Exams/m2014 q4i
一、题目要求
创建以下电路
二、分析
本题要求输出接地，使用assign语句即可，同时0在verilog中用1‘b0表示。代码如下
module top_module (
output out);
assign out=1'b0;
endmodule
三、仿真图
出现下图表示仿真成功
Exams/m2014 q4e
一、题目要求
创建以下电路
二、分析
电路表示的逻辑关系为或非，或为“|”，非为“~”。使用赋值语句assign连接输出和输入即可。代码如下
module top_module (
input in1,
input in2,
output out);
assign out=~(in1|in2);
endmodule
三、仿真图
出现下图表示仿真成功
Exams/m2014 q4f
一、题目要求
创建以下电路
二、分析
此电路的输出为输入in1和in2的非再进行与操作。与用“&”，输出和输入的连接使用assing语句即可，代码如下
module top_module (
input in1,
input in2,
output out);
assign out=in1 & (~in2);
endmodule
三、仿真图
出现下图表示仿真成功
Exams/m2014 q4g
一、题目要求
创建以下电路
二、分析
本题为in1和in2的同或得到的结果再与in3异或。verilog里边异或用“^”，同或为异或的非。输出和输入使用赋值语句即可，代码如下
module top_module (
input in1,
input in2,
input in3,
output out);
assign out=(~(in1^in2)) ^ in3;
endmodule
三、仿真图
出现下图表示仿真成功
Gates
一、题目要求
创建一个两输入的组合电路，其中输出分别为以下逻辑关系。
out_and: a and b
out_or: a or b
out_xor: a xor b
out_nand: a nand b
out_nor: a nor b
out_xnor: a xnor b
out_anotb: a and-not b
二、分析
这里主要是一些逻辑关系的运算，其中需要注意的是n表示取反的意思，nand是指先与再反。然后这里xor是异或的意思，xnor为同或，a and-not b表示a和b非的与。组合逻辑电路，使用assign赋值即可。代码如下
module top_module(
input a, b,
output out_and,
output out_or,
output out_xor,
output out_nand,
output out_nor,
output out_xnor,
output out_anotb
);
assign out_and=a&b;
assign out_or=a|b;
assign out_xor=a^b;
assign out_nand=~(a&b);
assign out_nor=~(a|b);
assign out_xnor=~(a^b);
assign out_anotb=a&(~b);
endmodule
三、仿真图
7420
一、题目要求
创建下图所示的组合逻辑电路。
二、分析
根据模块图，可以看出，p1y是p1a，p1b，p1c，p1d四个输入的与非，p2y是p2d，p2c，p2b，p2a四个输入的与非，组合电路连接使用赋值语句assign即可，代码如下
module top_module (
input p1a, p1b, p1c, p1d,
output p1y,
input p2a, p2b, p2c, p2d,
output p2y );
assign p1y = ~(p1a & p1b & p1c & p1d);
assign p2y = ~(p2d & p2c & p2b & p2a);
endmodule
三、仿真图
Truthtable1
一、题目要求
创建一个实现下图真值表的组合电路。
二、分析
题目要求根据真值表设计一个组合电路。这里有两种思路，一种是利用卡诺图化简（数电知识），得到输出跟输入的最简逻辑表达式。一种是利用列举的方法，用if或者case语句判断输入的情况，得到输出的结果。例如如果输入为000，则输出为0。卡诺图化简如下图所示。
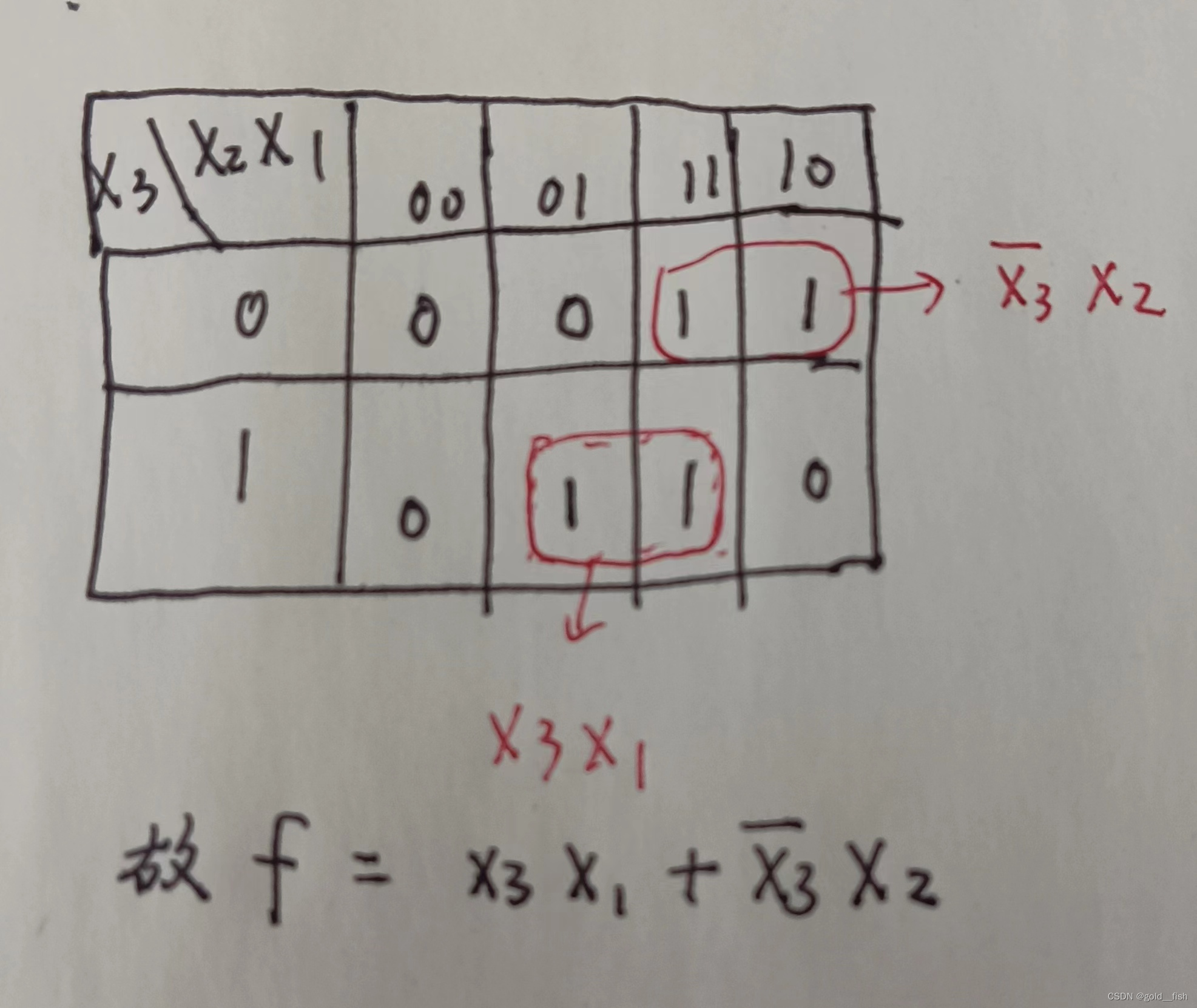
代码如下（注释部分为卡诺图化简的表达式，这里使用case语句，也可以尝试if语句）
module top_module(
input x3,
input x2,
input x1, // three inputs
output f // one output
);
always @(*)
begin
case({x3,x2,x1})
3'd0:f=1'b0;
3'd1:f=1'b0;
3'd2:f=1'b1;
3'd3:f=1'b1;
3'd4:f=1'b0;
3'd5:f=1'b1;
3'd6:f=1'b0;
3'd7:f=1'b1;
endcase
end
//assign f=(x3&x1) | ((~x3)&x2);
endmodule
三、仿真图
Mt2015 eq2
一、题目要求
创建一个有两个2位输入a[1:0]和B[1:0]的电路，并产生一个输出z。如果a = B, z的值应该是1，否则z应该是0。
二、分析
这里逻辑关系很简单，使用if语句判断即可。或者使用三目运算符。代码如下
module top_module ( input [1:0] A, input [1:0] B, output z );
//assign z=(A==B)?1'b1:1'b0;
always @(*)
begin
if(A==B)
z=1'b1;
else
z=1'b0;
end
endmodule
三、仿真图
出现下图表示仿真成功
Mt2015 q4a
一、题目要求
模块A应该实现函数z = (x^y) & x。
二、分析
创建一个组合逻辑电路实现上述功能。代码如下
module top_module (input x, input y, output z);
assign z = (x^y) & x;
endmodule
三、仿真图
出现下图表示仿真成功
Mt2015 q4b
一、题目要求
根据下列波形图创建电路。
二、分析
x，y为1位的输入，二者组合有四种情况，根据波形图得到下列真值表。
| x | y | z |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
这里可以很直接的看出，输出z是输入x，y的同或，即输入相同输入为1，输入不同输出为0。也可以画卡诺图或者利用if语句，case语句等，这里使用x，y同或，代码如下
module top_module ( input x, input y, output z );
assign z=~(x^y);
endmodule
三、仿真图
Mt2015 q4
一、题目要求
创建下图所示的电路。
二、分析
这里用到了mt2015_q4a 和 mt2015_q4b 里边的两个逻辑关系，即A表示的逻辑关系是mt2015_q4a 里边的z = (x^y) & x，B表示的逻辑关系是mt2015_q4b里边的z=~(x ^ y)。这样我们可以定义wire类型的变量来存储每一级的输出结果。代码如下
module top_module (input x, input y, output z);
wire wire1,wire2,wire3,wire4,wire5,wire6;
assign wire1 = (x^y) & x;//IA1
assign wire2 = ~(x ^ y);//IB1
assign wire3 = (x^y) & x;//IA2
assign wire4 = ~(x ^ y);//IB2
assign wire5 =wire1 | wire2;//IA1,IB1或
assign wire6 =wire3 & wire4 ;//IA2,IB2与
assign z = wire5 ^ wire6;
endmodule
三、仿真图
出现下图表示仿真成功
Ringer
一、题目要求
假设你正在设计一个电路来控制手机的铃声和振动电机。当电话需要接听来电(输入铃声)时，你的电路必须要么打开铃声(输出铃声= 1)，要么打开电机(输出电机= 1)，但不能同时打开。如果手机处于振动模式(输入vibrate_mode = 1)，打开电机。否则，打开铃声。
尝试只使用赋值语句，看看是否可以将问题描述转换为逻辑门的集合。
二、分析
这里输入信号有两个，分别是ring（手机响铃），和vibrate_mode（手机振动），输出信号有两个ringer（输出铃声），和motor（电机）。这里主要是ring和ringer不好理解。题目意思是说，如果ring=1，要么ringer=1，要么motor=1，“要么，要么表示或”，但又不能同时为1。如果vibrate_mode=1.那么motor=1，否则，ringer=1。为方便理解，画出真值表如下
| ring | vibrate_mode | ringer | motor |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
我们知道，输入信号有N个，那么真值表最多有2^N行，并且根据题目的意思，ring=1，要么ringer=1，要么motor=1，又不能同时为1，这本身是有问题的，这样画出的真值表有五行，说明思路错了。
这里比较容易确定的是输入都为0时，输出都为0。如果输入都为1，那么首先，motor=1是没问题的，那么ringer呢，题目说了ring=1，输出是不能同时为1的，那么ringer只能等于0。
关键在于ring和vibrate_mode仅有一个有效时，输出的情况。原文为：Suppose you are designing a circuit to control a cellphone’s ringer and vibration motor. Whenever the phone needs to ring from an incoming call (input ring), your circuit must either turn on the ringer (output ringer = 1) or the motor (output motor = 1), but not both. If the phone is in vibrate mode (input vibrate_mode = 1), turn on the motor. Otherwise, turn on the ringer.
原文最后一句话说如果vibrate_mode=1，motor=1，否则，ringer=1。这样得到下列真值表
| ring | vibrate_mode | ringer | motor |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
则ringer=ring&(~vibrate_mode)，motor=ring&vibrate_mode。
仿真后知道，此表达式正确，代码如下
module top_module (
input ring,
input vibrate_mode,
output ringer, // Make sound
output motor // Vibrate
);
assign ringer = ring & ~vibrate_mode;
assign motor = ring & vibrate_mode;
endmodule
故根据真值表，原文应该这样理解，ringer或者vibrate_mode中有一个为1时，ring就等于1。并且ringer和vibrate_mode不会同时为1。如果vibrate_mode=1，那么motor=1。vibrate_mode=1，motor=1是在ring=1条件下的，因为根据真值表第二行，即便vibrate_mode=1了motor也没有等于1。
注：如果各位读者实在想不出本题或者是很难理解原文的话。这里有一个很取巧的做法，因为HDLBits在没有语法错误的时候，如果最后的结果给你波形图的，系统会自动给输入赋值，你可以看你的输出和正确答案的输出。如果最后的结果没有波形图的话，此法不管用。比如这里我随便写下边的代码
module top_module (
input ring,
input vibrate_mode,
output ringer, // Make sound
output motor // Vibrate
);
assign ringer=ring&vibrate_mode;
assign motor = ring;
endmodule
得到以下波形图
inputs是系统自动给的输入组合，yours表示你的输出，ref表示正确的输出。这里你可以根据inputs和ref列出真值表或者其他方法就能得到输出和输入的关系式。
三、仿真图
Thermostat
一、题目要求
设置一个恒温器电路，控制打开和关闭加热器（heater）、空调（aircon）和鼓风机（fan）。
恒温器有两种模式:加热模式(mode = 1)和冷却模式(mode = 0)
在加热模式下(mode=1)，当温度过低(too_cold = 1)时打开加热器（heater=1），但不使用空调（aircon=0）。
在制冷模式下（mode=0），当温度过高(too_hot = 1)时，打开空调（aircon=1），但不要打开暖气（heater=0）。
当加热器或空调打开（heater=1或aircon=1）时，也要打开风扇（fan=1），让空气流通。此外，用户还可以要求打开风扇(fan_on = 1)，即使加热器和空调关闭。
要求只使用赋值语句
二、分析
module top_module (
input too_cold,
input too_hot,
input mode,
input fan_on,
output heater,
output aircon,
output fan
);
可以看到，模块给了四个输入，三个输出。最简单且高效的就是列出真值表，找出输出和输入的关系（数电应该有学过根据逻辑描述得到逻辑关系式）。真值表这里暂不分析，逻辑比较简单。逐个分析如下
heater：heater要输出1，需要两个条件，一个是处于加热模式（mode=1）且温度过低（too_cold=1），由“且”可以知道逻辑关系为“&”，故heater=mode&too_cold（即当mode和too_cold都为真时，heater=1）
aircon:aircon要输出1，需要两个条件，一个是处于制冷模式（mode=0）且温度过高（too_hot=1）
由“且”可以知道逻辑关系为“&”，故aircon=（~mode）&too_cold（即当mode假且too_cold为真时，aircon=1）
fan：fan要输出1，有三种情况，要么加热器或空调打开（heater=1或aircon=1），用户要求打开风扇(fan_on = 1)，即使加热器和空调关闭（意思是只要fan_on=1,不管heater和aircon的状态，即只跟fan_on有关）。根据“要么”，“或”可以知道逻辑关系为“或”。故fan=fan_on|(mode&too_cold)|(（~mode）&too_cold)。注意加热器或制冷器打开时的逻辑表达式。
电路要求只使用赋值语句，即assign，代码如下：
module top_module (
input too_cold,
input too_hot,
input mode,
input fan_on,
output heater,
output aircon,
output fan
);
assign heater = too_cold & mode;
assign aircon = too_hot & (~mode);
assign fan = fan_on | (too_cold & mode) | (too_hot & (~mode));
endmodule
三、仿真图
Popcount3
一、题目要求
“总体计数”电路计算输入向量中“1”的数量。为一个3位输入向量建立一个总体计数电路。
二、分析
总数计数电路，能够计算输入向量中“1”的个数。题目要求设计三位输入的电路，计算输入“1”的个数。
真值表如下（斜线左边为二进制表示法，右边加粗为十进制表示法）：
| in[2:0] | Out[1:0] |
|---|---|
| 000/0 | 00/0 |
| 001/1 | 01/1 |
| 010/2 | 01/1 |
| 011/3 | 10/2 |
| 100/4 | 01/1 |
| 101/5 | 10/2 |
| 110/6 | 10/2 |
| 111/7 | 11/3 |
根据真值表可以知道，输入有8种情况，可以全部列举出来，使用case语句来选择in[2:0]的内容，对应输出out[1:0]的值。代码如下（十进制表示法）：
module top_module(
input [2:0] in,
output [1:0] out );
always @(*)
begin
case(in)
3'd0:out=2'd0;
3'd1:out=2'd1;
3'd2:out=2'd1;
3'd3:out=2'd2;
3'd4:out=2'd1;
3'd5:out=2'd2;
3'd6:out=2'd2;
3'd7:out=2'd3;
endcase
end
endmodule
输入较少时，可以用列举法，但是输入较多如何处理，总不能也全部列举完吧，有没有什么简单点的方法？
因为只需要计算‘1’的个数，不需要知道1具体在哪里，即假设有一个‘1’，那么不管‘1’出现在in[2]，in[1]还是in[0]，out的输出都为1，那么可以只考虑输入在各个in[2:0]位的‘1’即可。因为in[i]，i=0,1,2的值如果是1，那么out值加1，如果是0，out的值加0，即不加（不变）。然后把输入的所有位都判断完，输出结果。
所以，利用for循环逐位判断输入是否为1，需要定义一个中间变量reg类型out1来暂存‘1’的个数值，如果是1，则out1加1，0则不变，最后将out1的值赋给out即可。这里在always里边，out1不能使用非阻塞赋值（<=）,否则会报错，因为我们需要在判断完in[i]的值以后，马上给out1赋值，而不是等块结束以后才赋值。这里没有涉及时序逻辑，不需要使用非阻塞赋值。
代码如下：
module top_module(
input [2:0] in,
output [1:0] out );
reg [1:0] out1;
always @(*)
begin
out1=2'b0;
for(integer i=0;i<3;i++)
if(in[i]==1'b1)
out1=out1+1'b1;
else
out1=out1;
end
assign out=out1;
endmodule
相比于第一种，for循环可以处理的输入多并且逻辑清晰，推荐第二种方法。
三、仿真图
Gatesv
一、题目要求
给你一个4位的输入向量[3:0]。我们想知道每个比特和它的邻居之间的关系:
out_both:这个输出向量的每一位都应该表明对应的输入位和它左边的邻居(更高的下标)是否都是“1”。例如，out_both[2]应该表示[2]和[3]中是否都是1。因为在[3]中左边没有邻居，所以答案很明显，所以我们不需要知道out_both[3]。
out_any:这个输出向量的每一位都应该表明是否有任何对应的输入位和它右边的邻居是“1”。例如，out_any[2]应该指示[2]或[1]中的任何一个为1。因为在[0]中右边没有邻居，所以答案很明显，所以我们不需要知道out_any[0]。
out_different:这个输出向量的每一位都应该表明对应的输入位与它左边的邻居是否不同。例如，out_different[2]应该表示[2]中的内容与[3]中的内容是否不同。对于这一部分，将向量视为环绕，因此[3]中左边的邻居在[0]中。
二、分析
给你一个四位的输入in[3:0]，找出它们每一位跟相邻位的关系。
out_both[2:0]：这个输出向量的每一位都应该表明对应的输入位和它左边的邻位(高一位)是否都是“1”。比如out_both[i]，表示in[i],in[i+1]是否都为1，i=0，1，2。都是1要求使用逻辑‘与’，符号为“&”。
out_any[3:1]：这个输出向量的每一位都应该表示对应的输入位及其右边的邻位（低一位）两位中是否有一个为“1”。即out_any[i]表示in[i],in[i-1],是否都为1，其中i=3，2，1。都是1要求使用逻辑‘或’，符号为“|”。
Out_different[3:0]：这个输出向量的每一位都应该表明对应的输入位与它左边的邻位（高一位）是否不同。例如，out_different[2]应该表示[2]中的内容与[3]中的内容是否不同。对于这一部分，需要将输入向量视为环绕，也就是in[3]中左边的邻位时in[0],in[0]右边的邻位是in[3]。这里要求‘不同’，即两位不同为1，同为0，可以想到使用逻辑‘异或’，符号为”^“。
代码如下
法一：直接赋值。代码如下：
module top_module(
input [3:0] in,
output [2:0] out_both,
output [3:1] out_any,
output [3:0] out_different );
assign out_both[2]=in[2]&in[3];
assign out_both[1]=in[1]&in[2];
assign out_both[0]=in[0]&in[1];
assign out_any[3]=in[3]|in[2];
assign out_any[2]=in[2]|in[1];
assign out_any[1]=in[1]|in[0];
assign out_different[3]=in[3]^in[0];
assign out_different[2]=in[2]^in[3];
assign out_different[1]=in[1]^in[2];
assign out_different[0]=in[0]^in[1];
endmodule
法二：使用for循环
module top_module(
input [3:0] in,
output [2:0] out_both,
output [3:1] out_any,
output [3:0] out_different );
always @(*)begin
for(integer i=0;i<3;i++)begin
out_both[i]=in[i]&in[i+1];
out_any[i+1]=in[i+1]|in[i];
out_different[i]=in[i]^in[i+1];
end
end
assign out_different[3]=in[3]^in[0];
endndmodule
注：for循环可以简化程序，当输入向量个数较大时，比直接赋值方便。单独给out_different[3]赋值是因为循环不好处理，如果有更好的写法，欢迎交流。
三、仿真图
Gatesv100
一、题目要求
在[99:0]中给你一个100位的输入向量。我们想知道每个比特和它的邻居之间的关系:
out_both:这个输出向量的每一位都应该表明对应的输入位和它左边的邻居是否都是“1”。例如，out_both[98]应该表示[98]和[99]中是否都是1。因为in[99]左边没有邻居，所以答案很明显，所以我们不需要知道out_both[99]。
out_any:这个输出向量的每一位都应该表明是否有任何对应的输入位和它右边的邻居是“1”。例如，out_any[2]应该指示[2]或[1]中的任何一个为1。因为在[0]中右边没有邻居，所以答案很明显，所以我们不需要知道out_any[0]。
out_different:这个输出向量的每一位都应该表明对应的输入位与它左边的邻居是否不同。例如，out_different[98]应该表示[98]中是否与[99]中不同。对于这一部分，将向量视为环绕，因此在[99]中左侧的邻居在[0]中。
二、分析
给你一个一百位的输入in[99:0]，找出它们每一位跟相邻位的关系。（本题同上一题，只是输入向量个数变到100个，用for循环处理）
out_both[98:0]：这个输出向量的每一位都应该表明对应的输入位和它左边的邻位(高一位)是否都是“1”。比如out_both[i]，表示in[i],in[i+1]是否都为1，i=0，1，2。都是1要求使用逻辑‘与’，符号为“&”。
out_any[99:1]：这个输出向量的每一位都应该表示对应的输入位及其右边的邻位（低一位）两位中是否有一个为“1”。即out_any[i]表示in[i],in[i-1],是否都为1，其中i=3，2，1。都是1要求使用逻辑‘或’，符号为“|”。
Out_different[99:0]：这个输出向量的每一位都应该表明对应的输入位与它左边的邻位（高一位）是否不同。例如，out_different[2]应该表示[2]中的内容与[3]中的内容是否不同。对于这一部分，需要将输入向量视为环绕，也就是in[3]中左边的邻位时in[0],in[0]右边的邻位是in[3]。这里要求‘不同’，即两位不同为1，同为0，可以想到使用逻辑‘异或’，符号为”^“。
代码如下：
module top_module(
input [99:0] in,
output [98:0] out_both,
output [99:1] out_any,
output [99:0] out_different );
always @(*)begin
for(integer i=0;i<99;i++)begin
out_both[i]=in[i]&in[i+1];
out_any[i+1]=in[i+1]|in[i];
out_different[i]=in[i]^in[i+1];
end
end
assign out_different[99]=in[99]^in[0];
endmodule
三、仿真图
出现下图表示仿真成功
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
