【机器学习chp14 — 总】生成式模型大全—扩散模型Diffusion、生成对抗网络GAN、变分自编码器VAE（草履虫都能看懂，超详细分析，易于理解，推导严谨，一文就够了）

生成式模型的一个核心优势在于能够通过概率分布来表达多样性。例如，输入一幅鸟的图像经过分类器输出标签“Bird”是确定的；而输入“Bird”（鸟）的概念到生成器中，则可以生成多种不同样式、角度、颜色的鸟图像。
这种多样性通常通过引入随机变量（例如颜色、角度、背景等）来控制，从而使生成的结果具有“创造力”。

绘画场景： 输入描述“红眼的角色”，模型可以生成多个不同风格或构图的图像。
聊天机器人： 针对作文题目或对话输入，生成的文本可以体现不同的表达风格和细节。

（2）神经网络作为生成器

生成式模型常常采用神经网络作为生成器。模型接收来自简单分布（如正态分布）的随机样本 $z$ 作为输入，然后映射到复杂的生成分布 $P_G$ 。目标是使生成器输出的数据尽可能接近真实数据分布 $P_{\text{data}}$ ：

$z \sim \mathcal{N}(0, I) \quad\rightarrow\quad x = G_\theta(z) \quad\text{or} \quad x \sim P_G \approx P_{\text{data}}$

这正是如生成对抗网络（GAN）和变分自编码器（VAE）中常见的思想。

3、生成式模型的目标：极大似然与KL散度

（1）极大似然估计（Maximum Likelihood）

生成式模型的目标之一是使生成的数据和真实数据“看起来像”。这通常通过极大似然估计（MLE）来实现。给定真实数据样本 $\{x_i\}_{i=1}^N$ ，我们希望最大化对数似然：

$\theta^* = \arg\max_\theta \frac{1}{N}\sum_{i=1}^N \log P_\theta(x_i)$

这意味着在真实数据分布下，生成数据的概率要尽可能高。

（2）KL 散度的最小化

极大似然估计等价于最小化真实数据分布 $P_{\text{data}}$ 与模型分布 $P_\theta$ 之间的 KL 散度：

$\theta^* = \arg\min_\theta \operatorname{KL}(P_{\text{data}} \,\|\, P_\theta) = \arg\min_\theta \mathbb{E}_{x\sim P_{\text{data}}}\left[-\log P_\theta(x)\right]$

直观上，KL 散度衡量了两个分布的“距离”，最小化它可以使模型生成的数据分布尽量接近真实数据分布。

4、基于能量的模型及其参数学习

（1）能量模型描述

在很多情况下，我们不需要直接获得绝对概率，只需要相对概率即可。基于能量的模型给出如下形式：

$P_\theta(x) = \frac{e^{-E_\theta(x)}}{Z_\theta}$

其中：

$E_\theta(x)$ 是能量函数，反映了样本 $x$ 的“能量”或“代价”。
$Z_\theta = \int_x e^{-E_\theta(x)}dx$ 是归一化常数（分区函数），保证 $P_\theta(x)$ 为概率分布。

（2）对数似然及其梯度

在极大似然框架下，对数似然为：

$\log P_\theta(x) = -E_\theta(x) - \log Z_\theta$

对参数 $\theta$ 求梯度得到：

$\nabla_\theta \log P_\theta(x) = -\nabla_\theta E_\theta(x) - \nabla_\theta \log Z_\theta$

其中， $\nabla_\theta \log Z_\theta$ 可进一步推导：

$\nabla_\theta \log Z_\theta = \frac{1}{Z_\theta} \nabla_\theta Z_\theta$

注意到

$Z_\theta = \int_x e^{-E_\theta(x)} dx \quad \Rightarrow \quad \nabla_\theta Z_\theta = -\int_x e^{-E_\theta(x)} \nabla_\theta E_\theta(x) dx$

因此，

$\nabla_\theta \log Z_\theta = -\frac{1}{Z_\theta} \int_x e^{-E_\theta(x)} \nabla_\theta E_\theta(x)dx = -\mathbb{E}_{x\sim P_\theta}[\nabla_\theta E_\theta(x)]$

代回原式，我们得到：

$\nabla_\theta \log P_\theta(x) = -\nabla_\theta E_\theta(x) + \mathbb{E}_{x\sim P_\theta}[\nabla_\theta E_\theta(x)]$

对整个数据分布 $P_{\text{data}}$ 取期望，即参数更新的梯度为：

$\nabla_\theta \mathbb{E}_{x\sim P_{\text{data}}}[\log P_\theta(x)] = -\mathbb{E}_{x\sim P_{\text{data}}}[\nabla_\theta E_\theta(x)] + \mathbb{E}_{x\sim P_\theta}[\nabla_\theta E_\theta(x)]$

这就给出了模型中两个重要的项：

数据项：从真实数据分布中采样，推动能量函数降低，使真实数据的能量更低。
模型项：从当前模型分布中采样，推动能量函数升高，使模型生成的低能量区域不泛滥。（不同的模型比如下面的VAE和GAN的这一项不一样）

（3）近似计算与采样问题

在实际应用中，从 $P_\theta$ 采样往往计算代价较高，因此需要近似方法来计算第二项的梯度。常用的方法包括：

马尔可夫链蒙特卡洛（MCMC）
对比散度（Contrastive Divergence）

近似梯度可以写成：

$\nabla_\theta \mathbb{E}_{x\sim P_{\text{data}}}[\log P_\theta(x)] \approx -\frac{1}{N}\sum_{i=1}^{N} \nabla_\theta E_\theta(x_i) + \frac{1}{N}\sum_{i=1}^{N} \nabla_\theta E_\theta(\hat{x}_i)$

其中 $x_i \sim P_{\text{data}}$ 而 $\hat{x}_i \sim P_\theta$ 通过某种采样方法得到。这种方法能够在一定程度上平衡真实数据和模型生成数据之间的差异，从而不断调整参数，使得 $P_\theta$ 渐进地逼近 $P_{\text{data}}$ 。

5、总结

生成式模型通过以下几个关键步骤构建与学习数据分布：

从确定性映射到概率映射：传统神经网络映射 $X \rightarrow Y$ 被扩展为 $X \rightarrow P(Y)$ ，允许输出多样化结果。
模型多样性与创造性：通过引入随机性（例如随机变量 $z$ ）生成不同样式的输出，从而满足如图像生成、文本生成等任务的“创造力”需求。
极大似然估计与KL散度：利用极大似然原理最大化真实数据的似然，等价于最小化真实分布与模型分布间的 KL 散度。
能量模型的框架：用能量函数 $E_\theta(x)$ 和归一化常数 $Z_\theta$ 定义概率分布，重点关注相对概率关系。
参数学习与梯度推导：推导出对数似然的梯度包含两个项——真实数据项和模型采样项，进而通过近似采样（如 MCMC 或对比散度）进行参数更新。

这种从简单分布到复杂数据分布的映射，不仅揭示了生成式模型的数学本质，也为如何训练能够生成多样化、真实感强的样本提供了理论依据和实践方法。

通过以上分析，我们可以看出生成式模型的核心在于如何将神经网络从传统的确定性映射扩展到概率建模，并利用极大似然、能量函数和采样方法等工具，实现对复杂数据分布的有效学习。

二、变分自编码器 VAE

1、自编码器 AE

核心思想：可以看成PCA的神经元网络化。

（1）自编码器的基本结构与目标

1.1 编码器-解码器结构

图中，可以看到自编码器的典型结构：

输入层：原始输入 $\mathbf{x}$ （例如一张图像或一段向量）。
编码器（Encoder）：一系列神经网络层，将高维的 $\mathbf{x}$ 压缩到低维的隐藏表示 $\mathbf{z}$ （也称潜在表示，latent representation）。
解码器（Decoder）：与编码器结构相对称或相似的网络，将低维的 $\mathbf{z}$ 还原回与输入同维度的 $\mathbf{x}'$ （即重构的结果）。
输出层：得到的重构 $\mathbf{x}'$ 。

整个过程可用下式概括：

$\mathbf{z} = f_{\text{enc}}(\mathbf{x}), \quad \mathbf{x}' = f_{\text{dec}}(\mathbf{z})$

1.2 目标函数：重构误差最小化

自编码器的目标函数：

$J(g, f) = \sum_i \|\mathbf{x}_i - \mathbf{x}_i'\|^2 + \lambda R(f)$

其中：

$\mathbf{x}_i - \mathbf{x}_i'\|^2$ 表示第 $i$ 个样本的重构误差（常见的是均方误差）。
$\lambda R(f)$ 是正则化项，用于约束网络的复杂度（例如权值衰减、稀疏性正则等）。

自编码器通过最小化重构误差来学习到一个对输入数据具有“良好”表示的隐藏向量 $\mathbf{z}$ ，使得在压缩后仍能较好地重构出原输入。

（2）自编码器与 PCA 的对比

2.1 PCA 与线性降维

对比了 PCA（主成分分析） 与自编码器在降维上的效果：

PCA：将原始数据通过线性映射（即正交变换）投影到方差最大的几个主成分上，实现降维。
自编码器：使用非线性神经网络进行编码和解码，能学习到更灵活、更丰富的表示。

从图中可以看到，在手写数字（如 0,1,2,3,4,9）上进行降维后，自编码器可以重构出更逼近原图的数字；而 PCA 由于其本质是线性映射，重构往往缺乏非线性特征的捕捉能力，因此在复杂数据上可能效果有限。

2.2 非线性映射的优势

自编码器通过多层感知机或卷积网络等方式实现编码-解码，可以学习到数据的非线性结构。对 MNIST 这种手写数字数据来说，每个数字都有不同的笔迹、线条弧度和书写风格，使用非线性模型更能捕捉到这种多样性，因此重构更好，潜在空间的分布也更有区分度。

（3）自编码器在降维与表示学习中的意义

通用性
图片中的示例主要是手写数字，但自编码器对其他高维数据（如图像、文本、推荐系统的用户-物品矩阵等）也适用。只要能定义合适的网络结构和损失函数，就可以把任何高维输入映射到较低维度的潜在空间进行分析和重构。
非线性表示学习
自编码器的编码器部分可以视为一个特征提取器，它能够在隐藏层中学习到对数据分布更有表达力的特征。这些特征在后续分类、聚类或检索等任务中往往表现优于简单的线性降维方法。
可视化
当将自编码器的中间层（特别是瓶颈层）的维度设为 2D 或 3D 时，就可以直接用来可视化数据在低维空间的分布，便于理解数据内部的结构和模式。
与正则化的结合
在第一张图的公式中可以看到正则化项 $\lambda R(f)$ 。常见的扩展包括：
- 稀疏自编码器（Sparse AE）：鼓励隐藏单元大部分为零激活；
- 去噪自编码器（Denoising AE）：对输入添加噪声再重构；
- 变分自编码器（VAE）：在潜在空间上引入概率分布假设；
  这些方法都能让模型学到更具泛化能力或更具解释性的表示。

2、变分自编码器 VAE

（1）生成式模型与变分自编码器概述

生成式模型的目标是学习数据的分布，从而能够生成与真实数据相似的新样本。变分自编码器（Variational Autoencoder, VAE）是其中一种重要的生成模型，它将传统自编码器的框架与概率模型和变分推断方法相结合，不仅能够重构输入数据，还能从隐变量空间中生成新的数据。与对抗生成网络（GAN）相比，VAE具有明确的概率解释和连续平滑的潜在空间，使其在一些需要不确定性估计或潜在特征表达的任务中表现突出。

（2）模型结构

2.1 编码器（Inference Network）

结构分析：在VAE中，编码器的输出是一个分布 $q(z|x)$ ， $c_1,c_2,c_3\cdot \cdot \cdot$ 为在一个分布 $q(z|x)=N(\mu (x),\sigma (x))$ 中采样得到的值。相比于AE，VAE编码器不再是一个神经元网络直接从输入映射到 z ，而是产生一个分布（即一个 $\mu$ ，一个 $\sigma$ ，而且这个 $\sigma$ 还有一定的随机性），再从这个分布中采样得到 z 。
功能：将输入数据 $x$ 映射到潜在空间，并构造近似后验分布 $q(z|x)$ 。
输出：通常输出隐变量分布的参数（例如均值 $\mu(x)$ 和方差 $\sigma^2(x)$ ），假设 $q(z|x)$ 为高斯分布。
意义：通过对输入数据进行编码，提取数据中的潜在特征，同时为后续的重构提供必要的隐变量信息。
编码器示意图如下：

2.2 解码器（Generative Network）

功能：根据从隐变量分布中采样得到的 $z$ 重构输入数据，建模条件分布 $p(x|z)$ 。
生成：利用解码器网络，可以从连续的潜在空间中采样，生成新的数据样本。
意义：实现数据的重构和生成，是VAE作为生成式模型的核心部分。

（3）VAE 的解码器的核心思想

3.1 回忆高斯混合模型

图片中显示了一个数据分布 $p(x)$ ，由多个高斯分布（曲线）混合而成。
数学表达式： $p(x) = \sum_z p(x|z)p(z)$ , 其中 $z$ 通常是一个离散的混合分量（整数索引）， $p(z)$ 为混合系数（满足多项分布），而 $p(x|z)$ 为第 $z$ 个高斯分布 $\mathcal{N}(\mu_z, \sigma _z)$ 。
直观来说，这个模型假设数据 $x$ 可能来自若干个不同的“子分布”（每个子分布是一个高斯），并用这些高斯分布的线性加权求和来近似整体分布。
局限性：当数据分布过于复杂时，仅依靠少量高斯分量可能难以逼近；若增加分量数，模型复杂度也随之增加。

3.2 高斯混合模型的扩展-VAE解码器

图片中显示了一个数据分布 $p(x)$ ，由无数个高斯分布（曲线）混合而成。计算 $p(x)$ 的过程就是解码的过程
数学表达式： $p(x) = \int p(x|z)p(z)dz$ , 其中隐变量 $z$ 并非离散，而是可以在连续空间中取值。， $p(z)$ 为混合系数（先验一般取标准正态分布 $z \sim \mathcal{N}(0,I)$ ，即初始值），而 $p(x|z)$ 为第 $z$ 个高斯分布 $\mathcal{N}(\mu_z,\sigma _z)$ （参数通过神经网络学）。
随着 $z$ 在连续空间中移动，解码器会生成一系列可能的 $x$ ，从而可以近似很多形状复杂的分布。
$p(z)$ 即是编码器中的 $q(z|x)$ 的先验，它是联系编码器与解码器的桥梁。
解码器示意图如下：

VAE整体结构图：

采样 $\rightarrow$

其中 $\mu (z)$ 和 $\sigma (z)$ 是输出分布（最大后验分布）的参数。 $\mu (z)$ 可视为重构的 $\hat{x}$ （最大似然值）。

（4）参数的训练

4.1 最大化似然函数

VAE的目标是最大化观测数据 $x$ 的似然 $p(x)$ ，即：

$p(x) = \int p(x|z) p(z) dz$

其中， $p(x|z)$ 是解码器生成 $x$ 的条件概率， $p(z)$ 是隐变量 $z$ 的先验分布（通常是标准正态分布 $\mathcal{N}(0, I)$ ）。然后，VAE的目标就是通过最大化 $p(x)$ 来学习一个好的生成模型。为了实现这一目标，我们通常优化其对数似然：

$l = \sum_x \ln(p(x))$

4.2 变分推断

直接最大化 $p(x)$ 是不可行的，因为计算 $\int p(x|z) p(z) dz$ 非常复杂。为了简化这个过程，VAE引入了变分推断。首先，我们引入一个变分分布 $q(z|x)$ ，它近似于后验分布 $p(z|x)$ 。因此，我们将对数似然的目标函数重写为：

$\ln p(x) = \int q(z|x) \ln p(x) dz$

这种重写是通过变分下界（Variational Lower Bound）实现的，它允许我们在无法直接计算后验分布的情况下，进行优化。

4.3 下界的推导

$\ln(p(x)) = \int q(z|x) \ln(p(x)) dz$

$= \int q(z|x) \left( \ln \frac{p(x,z)}{p(z|x)} \right) dz$

$= \int q(z|x) \left( \ln \frac{p(x,z)}{q(z|x)}\frac{q(z|x)}{p(z|x)} \right) dz$

$= \int q(z|x) \left( \ln \frac{p(x,z)}{q(z|x)} \right) dz + \int q(z|x) \left( \ln \frac{q(z|x)}{p(z|x)} \right) dz$

$= \int q(z|x) \left( \ln \frac{p(x,z)}{q(z|x)} \right) dz +\text{KL}(q(z|x)||p(z|x))$

而 $q(z|x)$ 本来就是 $p(z|x)$ 的近似，所以 $\text{KL}(q(z|x)||p(z|x)) \geq 0$ 且很接近于 0 .

所以得到 $\ln(p(x))$ 的下界 $\int q(z|x) \left( \ln \frac{p(x,z)}{q(z|x)} \right) dz$ ，记为 $\mathcal{L}_b$

4.4 优化目标

$\ln (p(x)) \approx \mathcal{L}_b$

$= \int q(z|x) \ln \frac{p(x, z)}{q(z|x)} dz$

$= \int q(z|x) \left( \ln p(x|z) + \ln p(z) - \ln q(z|x) \right) dz$

其可以拆成两部分：

重构项：
$\int q(z|x) \ln p(x|z) dz$
这是VAE模型中解码器的主要任务，它负责通过隐变量 $z$ 重构数据 $x$ 。
KL散度项：
$- \int q(z|x) \ln \frac{q(z|x)}{p(z)} dz$
这是VAE中的正则化项，确保编码器的近似后验 $q(z|x)$ 不偏离先验分布 $p(z)$ 过多。

为了优化VAE，我们最大化这个下界：

$\mathcal{L}_b = \mathbb{E}_{q(z|x)} [ \ln p(x|z) ] - D_{KL}(q(z|x) || p(z))$

其中：

第一个项 $\mathbb{E}_{q(z|x)} [ \ln p(x|z) ]$ 是重构误差，衡量通过解码器从隐变量 $z$ 重构原始数据 $x$ 的好坏。
第二个项 $D_{KL}(q(z|x) || p(z))$ 是KL散度，确保编码器输出的分布 $q(z|x)$ 与先验分布 $p(z)$ 之间的差异尽可能小。
我们希望第一项尽可能大，第二项前是减号，所以应尽可能小，第二项尽可能小就想要 $q(z|x)$ 尽可能接近标准正态分布，就意味着 z 没有任何辨识度，这样的话第一项就小了。而如果第一项大的话，预测就准确，此时 $q(z|x)$ 就不会太随机，第二项就不可能小了，所以这两部分的loss其实是相互拮抗的，要整体来看。（这部分的思想完完全全就是王木头所讲的，模型要在数据上误差最小，在未见过的数据上最大熵）

4.5 KL散度的最小化

KL散度是VAE优化的关键部分。它衡量了编码器输出的近似后验 $q(z|x)$ 与标准正态分布 $p(z) = \mathcal{N}(0, I)$ 之间的差异。为了最小化KL散度，编码器通过神经网络（如图中的NN'）输出隐变量 $z$ 的均值 $\mu'(x)$ 和标准差 $\sigma'(x)$ ，并学习一个合适的分布。

公式为：

$KL(q(z|x) || p(z)) = \frac{1}{2} \sum_{j=1}^{M} \left( \mu_j'^2 + \sigma_j'^2 - \log \sigma_j'^2 - 1 \right)$

这是一个标准的KL散度的闭式解，它会对每个维度的隐变量进行计算。

（5）VAE 相对于 AE 的优势

图中显示了 VAE（Variational AutoEncoder）中的编码器部分，具体包含了从输入到输出均值（ $\mu$ ) 和方差（ $\sigma^2$ ) 这两个步骤，以及后续的重参数化采样过程。

5.1 对噪声的建模

编码器通常由若干层神经网络组成，可以是多层感知器（MLP）或者卷积神经网络（CNN）等，具体取决于数据类型。
1. 图像：常用卷积层提取空间特征，然后 flatten 或全连接输出到隐变量的分布参数上。
2. 文本：常用RNN/LSTM/Transformer 等结构提取序列特征，再映射到分布参数上。
3. 其他数据：根据数据特点选择合适的网络结构。
输出
编码器输出并不是直接的隐变量 $\mathbf{z}$ ，而是隐变量分布（近似后验分布） $q(\mathbf{z}|\mathbf{x})$ 的参数，一般为均值向量 $\boldsymbol{\mu}(\mathbf{x})$ 和对数方差向量 $\log \boldsymbol{\sigma}^2(\mathbf{x})$ 。
这样做的原因是：VAE希望通过一个高斯分布来表示给定 $\mathbf{x}$ 后潜在变量 $\mathbf{z}$ 的不确定性，即
$q(\mathbf{z}|\mathbf{x}) = \mathcal{N}\bigl(\mathbf{z};\, \boldsymbol{\mu}(\mathbf{x}), \, \boldsymbol{\sigma}^2(\mathbf{x}) \mathbf{I}\bigr)$
学习到“噪声”的方差
图中“自动学习到噪声的方差”指的就是通过最小化KL散度和重构误差，让网络自动去适配合适的 $\boldsymbol{\sigma}(\mathbf{x})$ （即每个维度的标准差），从而平衡“让分布贴近标准正态先验”与“尽可能重构输入”的目标。
如果只是最小化重构误差，而没有让 z 的分布贴近标准正态分布，则方差为0，此时VAE等同于AE 。

（6）重参数化技巧

采样的难点
如果我们直接从 $\mathcal{N}\bigl(\boldsymbol{\mu}, \boldsymbol{\sigma}^2 \mathbf{I}\bigr)$ 中采样 $\mathbf{z}$ ，采样过程不可导，无法对编码器进行梯度更新。
重参数化
为了使采样过程可导，VAE中引入了重参数化技巧：
$\mathbf{z} = \boldsymbol{\mu}(\mathbf{x}) + \boldsymbol{\sigma}(\mathbf{x}) \,\odot\, \boldsymbol{\epsilon}$
其中 $\boldsymbol{\epsilon} \sim \mathcal{N}(0,\mathbf{I})$ 是从标准正态分布采样得到的噪声向量， $\odot$ 表示逐元素乘法。
好处
由于 $\boldsymbol{\mu}$ 和 $\boldsymbol{\sigma}$ 都是由可学习的神经网络（编码器）输出的， $\boldsymbol{\epsilon}$ 是与模型参数无关的随机噪声，因而我们可以对 $\boldsymbol{\mu}(\mathbf{x})$ 和 $\boldsymbol{\sigma}(\mathbf{x})$ 进行反向传播，学习到让模型最优的分布参数。

（7）编码器部分的目标：近似后验

近似后验分布 $q(\mathbf{z}|\mathbf{x})$
VAE的编码器本质上在做“变分推断”，它试图用一个高斯分布去近似真实的后验分布 $p(\mathbf{z}|\mathbf{x})$ 。
- 先验分布： $p(\mathbf{z}) = \mathcal{N}(0, \mathbf{I})$ （固定不变）。
- 后验分布： $p(\mathbf{z}|\mathbf{x})$ （难以直接计算）。
- 近似后验： $q(\mathbf{z}|\mathbf{x})$ （编码器输出），用神经网络来近似。
KL 散度
编码器要通过最小化KL散度 $D_{\mathrm{KL}}(q(\mathbf{z}|\mathbf{x})\|p(\mathbf{z}))$ 来保证自己输出的分布不会偏离先验分布过远，从而使得潜在空间具有良好的结构。同时，KL散度也会抑制 $\boldsymbol{\sigma}$ 不合理地变大或变小。

（8）VAE 总结

8.1 VAE整体流程概览

输入数据 $\mathbf{x}$ ：从训练集中获取样本（如图像、文本等）。
编码器（Encoder）：将 $\mathbf{x}$ 映射到潜在分布的参数（ $\boldsymbol{\mu}, \boldsymbol{\sigma}$ ），得到近似后验 $q(\mathbf{z}|\mathbf{x})$ 。
重参数化采样（Reparameterization Trick）：根据 $\boldsymbol{\mu}, \boldsymbol{\sigma}$ 以及标准正态噪声 $\boldsymbol{\epsilon}$ ，得到隐变量 $\mathbf{z}$ 。
解码器（Decoder）：从隐变量 $\mathbf{z}$ 生成或重构数据 $\mathbf{x}'$ ，对应分布 $p(\mathbf{x}|\mathbf{z})$ 。
计算损失并反向传播：包括
- 重构误差（衡量 $\mathbf{x}'$ 与 $\mathbf{x}$ 的差异）
- KL 散度（约束 $q(\mathbf{z}|\mathbf{x})$ 与先验 $p(\mathbf{z})$ 的接近程度）将这两项结合在一起形成VAE的训练目标（ELBO），通过反向传播同时更新编码器和解码器的参数。

8.2 编码器部分的详细步骤

输入 $\mathbf{x}$
- 将观测数据 $\mathbf{x}$ （图像像素、文本向量等）输入到编码器网络。
- 编码器可能是多层感知器（MLP）、卷积网络（CNN）、或其他合适的网络结构。
提取特征
- 编码器通过多层神经网络对输入数据进行特征提取，逐步将高维数据压缩到更紧凑的表示。
- 这些中间特征会为后续的分布参数输出做准备。
输出分布参数 $\boldsymbol{\mu}(\mathbf{x}), \log \boldsymbol{\sigma}^2(\mathbf{x})$
- 编码器的最终输出通常是两个向量：均值 $\boldsymbol{\mu}$ 和对数方差 $\log \boldsymbol{\sigma}^2$ （或直接输出 $\boldsymbol{\sigma}$ ）。
- 这两个向量共同决定了给定 $\mathbf{x}$ 后，隐变量 $\mathbf{z}$ 的近似后验分布 $q(\mathbf{z}|\mathbf{x})$ 。
重参数化采样（Reparameterization Trick）
1. 直接从 $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma}^2 \mathbf{I})$ 采样 $\mathbf{z}$ 不可导，无法对编码器进行梯度更新。
2. 因此使用重参数化： $\mathbf{z} = \boldsymbol{\mu}(\mathbf{x}) + \boldsymbol{\sigma}(\mathbf{x}) \odot \boldsymbol{\epsilon}$ ，其中 $\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})$
3. 这样采样过程可微，编码器网络就能在训练中被更新。
得到隐变量 $\mathbf{z}$
1. 最终，我们得到对 $\mathbf{x}$ 的隐变量表示 $\mathbf{z}$ 。
2. 这一步完成后， $\mathbf{z}$ 就可被解码器拿去生成重构。
梯度更新（与损失函数一起）
1. 编码器的参数在计算完重构损失和KL散度后，通过反向传播进行更新。
2. KL散度部分会鼓励编码器输出的 $q(\mathbf{z}|\mathbf{x})$ 贴近先验 $p(\mathbf{z})$ ，从而让潜在空间有良好结构。

8.3 解码器部分的详细步骤

输入隐变量 $\mathbf{z}$
1. 在训练阶段， $\mathbf{z}$ 来自编码器输出的近似后验；在生成阶段， $\mathbf{z}$ 来自先验分布 $p(\mathbf{z}) = \mathcal{N}(0,\mathbf{I})$ 。
多层神经网络映射
1. 解码器将 $\mathbf{z}$ 通过若干层非线性变换映射回数据空间。
2. 对图像而言，可能使用转置卷积（Deconv）逐步还原为像素；对文本可能使用RNN/Transformer等结构生成词序列。
输出分布或重构结果 $\mathbf{x}'$
1. 解码器的输出可以是：
  1. 分布参数：如对图像像素输出Bernoulli/Gaussian的参数，对文本输出词的softmax概率分布等；
  2. 直接的重构：如连续值的像素。
2. 这样就可以用对数似然或其它损失度量“重构”与真实数据的差异。
计算重构误差（Reconstruction Loss）
1. 根据解码器输出的分布 $\hat{p}(\mathbf{x}|\mathbf{z})$ 与真实数据 $\mathbf{x}$ ，计算负对数似然或交叉熵、MSE等。
2. 这个重构误差越小，表示解码器越能“还原”或“生成”逼近 $\mathbf{x}$ 的样本。
反向传播更新解码器参数
1. 解码器参数通过重构误差与KL散度（间接影响）的组合在ELBO目标下被优化。
2. 编码器和解码器协同训练，以在潜在空间和重构质量之间取得平衡。
生成新样本
1. 训练完成后，只需从先验 $\mathcal{N}(0,\mathbf{I})$ 采样 $\mathbf{z}$ ，输入解码器即可生成全新的样本 $\mathbf{x}'$ ，实现生成式建模。

8.4 训练与推断阶段的对比

训练阶段
- 编码器 + 解码器共同工作：
  1. 编码器根据输入 $\mathbf{x}$ 输出 $\boldsymbol{\mu}, \boldsymbol{\sigma}$ 。
  2. 重参数化采样得到 $\mathbf{z}$ 。
  3. 解码器根据 $\mathbf{z}$ 生成 $\mathbf{x}'$ 。
  4. 计算重构误差和KL散度，形成ELBO，反向传播更新参数。
推断/生成阶段
- 只需使用解码器部分：
  - 从先验分布采样 $\mathbf{z} \sim \mathcal{N}(0,\mathbf{I})$ 。
  - 输入解码器生成新样本 $\mathbf{x}'$ 。
- 无需真实数据 $\mathbf{x}$ 的参与，即可自由生成新样本。

（9）VAE的局限性

VAE 在实际使用中也暴露出了一些局限性或常见问题。

9.1 生成图像“模糊”或“平均化”问题

i、重构目标导致的模糊

高斯假设与像素级重构损失
在最常见的实现中，VAE 通常假设图像像素的条件分布为高斯分布（或近似用均方误差/MSE做重构损失）。
这在面对多模态或复杂图像细节时往往导致生成结果出现“模糊”或“平均化”的现象。
- 原因：当多个真实样本都可能对应相似的潜在向量 $\mathbf{z}$ 时，VAE 倾向输出一个平均（或折中）结果来最小化整体重构误差，导致缺乏锐度和细节。
多模态数据的平均化
例如，对于某些模态多样的图像（同一个潜在语义可能对应不同外观），VAE 在训练时可能更倾向于生成折中版本的图像，而无法像一些对抗式生成模型（GAN）那样更尖锐地选择某个模态。

ii、KL 散度与重构误差的平衡

在 VAE 的目标函数（ELBO）中，重构误差（ $-\mathbb{E}_{q(\mathbf{z}|\mathbf{x})}[\ln p(\mathbf{x}|\mathbf{z})]$ ）与 KL 散度（ $D_{\text{KL}}(q(\mathbf{z}|\mathbf{x}) \parallel p(\mathbf{z}))$ ）同时被优化。
有时为了减小 KL 散度，模型会让后验分布 $q(\mathbf{z}|\mathbf{x})$ 更贴近先验 $p(\mathbf{z})$ ，从而减少了潜在空间的灵活性，间接导致生成结果不够细腻或多样。

9.2 可能出现“记住”训练样本的倾向

i、重构训练集的图像

VAE 只要能对训练集中样本重构良好，就可以得到较低的重构损失。如果模型容量足够大，VAE 可能学到某些近似“记忆”训练集中图像的方式。
图中“7”的例子（只需改动极少像素即可与原图保持接近）就说明，VAE 有时会生成与训练集样本非常相似的结果，而非完全新的样本。

ii、多样性不足

由于解码器要在给定 $\mathbf{z}$ 时产生“尽量接近真实图像”的结果，且编码器又试图把不同 $\mathbf{x}$ 压缩到潜在空间中，如果没有额外的约束或正则，VAE 有时缺乏对“新颖样本”的探索，生成结果容易集中于训练数据的局部模式。

9.3 后验分布表达能力不足

i、因果：VAE 对后验分布的限制

在最基本的 VAE 中，后验分布 $q(\mathbf{z}|\mathbf{x})$ 被限制为各向同性高斯或对角高斯。
这种限制导致模型可能无法充分表达数据的潜在复杂性。对于非常复杂或多模态的数据，简单的高斯假设无法捕捉到真实后验的形状，从而影响生成质量和表示能力。

ii、Posterior Collapse（后验坍缩）

在某些情况下（尤其是文本生成、序列生成时），后验分布可能退化为与先验几乎相同，编码器几乎不使用输入信息， $\mathbf{z}$ 失去表达力。
这被称为“Posterior Collapse”，导致模型学习不到有用的潜在表示，生成质量也随之下降。

9.4 高维数据与高保真生成的挑战

i、VAE 对高分辨率图像的局限

对于分辨率较高、细节丰富的图像（如人脸、风景等），标准 VAE 通常很难生成细节清晰的结果。
研究者常需在网络结构、后验假设、损失函数上做更多改进（如使用 PixelVAE、PixelCNN 解码器、或分层 VAE），才能在高分辨率生成任务上取得更好效果。

ii、训练难度与网络设计

在高维数据上，如何设计合适的网络结构（例如更深层的 CNN、分层 VAE、流模型与 VAE 结合等）也成为一大挑战。
如果网络结构设计不当或优化不稳定，VAE 容易出现收敛慢、生成质量差等问题。

9.5 与 GAN 等其他生成模型的对比

i、生成逼真度

在很多视觉任务中，GAN（生成对抗网络）往往能生成更清晰、更逼真的图像。
相比之下，标准 VAE 在逼真度和细节方面可能稍显不足，易产生“模糊”感。

ii、模型目的与优势

当然，VAE 有自己独特的优势：可以显式估计数据似然，更容易在潜在空间进行插值、概率推断等；而 GAN 的判别器只提供一个对抗信号，并没有显式的似然估计。
但在“生成图像质量”这一点上，VAE 通常需要额外的改进（如 VAE-GAN、VQ-VAE、Glow 等）才能与 GAN 抗衡。

9.6 训练目标平衡与超参数敏感性

i、β-VAE 与权衡

为了平衡重构质量与潜在表示的解耦、通用性等，许多改进版本（如 β-VAE）在 ELBO 中引入可调节系数 β，控制 KL 散度项的权重。
但这也带来超参数调节的复杂性，且不同数据集和任务需要不同的超参数组合，影响模型性能。

ii、优化过程不稳定

虽然 VAE 的目标函数相比 GAN 更稳定（不需要对抗训练），但在高维场景或分层结构中，找到合适的学习率、批大小等也不易，模型易出现训练早期过拟合或后验坍缩等现象。

9.7 总结

模糊与平均化：VAE 常出现模糊的重构或生成图像，难以捕捉高频细节，容易产生平均化结果。
多样性不足：可能倾向记忆训练样本，或仅在训练集中样本周围做小改动，而不是生成真正新颖的样本。
后验表达能力有限：简单的高斯假设难以建模复杂分布，可能出现后验坍缩。
高维与高保真难度：在高分辨率、细节丰富的数据上，VAE 的重构或生成质量常不及对抗式模型，需要更多结构性改进。
与 GAN 对比：GAN 在图像逼真度上往往表现更好，而 VAE 在可解释性、潜在空间操作等方面有其优势。
超参数与优化：平衡重构和 KL 散度需要仔细调参，容易出现不稳定或训练不充分。

总的来说，VAE 并非“全能”的生成模型，在图像逼真度和多样性上仍存在不少挑战。但它的可解释性、对潜在空间的显式建模、以及与其他方法结合的潜力，依旧使其在许多研究方向中扮演着重要角色。后续的改进（如层级式 VAE、流模型结合、离散潜在变量、VQ-VAE 等）也在不断推进其生成能力与灵活性。

三、生成对抗网络 ( Generative Adversarial Networks，GAN )

1、GAN的基本思想

（1）生成器与判别器的基本结构与演变

生成器和判别器从初始（v1）到后续（v2、v3）的训练过程。

生成器：最初仅是一个简单的网络，从一个随机向量（通常采自正态分布）经过若干隐含层映射到图像空间。随着训练进行，网络从真实图像中学到更多，从而能够捕捉更复杂的数据分布，生成的图像也更接近真实。
判别器：最初作为一个简单的二分类器，任务是判断输入图像是真实数据还是生成器生成的假样本。随着版本升级，判别器的结构不断改进，能够更细致地区分细微的差异，提升整体判别能力。
生成器和判别器在对抗过程中不断升级、形成你追我赶的动态平衡。

（2）“对抗”机制及名词由来

训练过程中，生成器和判别器之间构成了一个博弈关系：

生成器试图生成越来越真实的样本以“欺骗”判别器；
判别器则努力区分真实样本与伪造样本，给予尽可能不同的评分。
这一对立关系可用下面的最小最大公式来描述（后面详细介绍）：

正是这种相互对抗的训练方式，使得整个系统能够不断提高生成质量，同时推动判别器不断进步。

（3）GAN 的核心思想

GAN 的核心思想是找到一个生成器 Generator 使得生成器接受一个正态分布的输入，它的输出的分布和真实数据的分布之间的差别最小，即：

$G^{*} =\underset{ G}{ argmin}Div(p_{G},p_{data})$

其中

$Div(p_{G},p_{data})$ 表示生成器生成的分布和真实数据分布之间的差异，div表示divergence，是散度的意思，但直接计算两个复杂分布之间的差异是一个很复杂的积分，所以有一个很方便的方法，就是采样sample，让从两个分布之中的采样尽可能地相近。

为什么只做sample，就可以估算出两个分布之间地 Div 呢？

这个就要靠判别器Discriminator 的力量。详细的在下文。

2、GAN训练的基本算法

（1）网络初始化与迭代更新框架

网络初始化
在训练开始前，需要对生成器 G 和判别器 D 进行参数初始化。保证两个网络从随机状态开始。

同时，每轮训练过程使用的真实数据集是在总的真实数据集中随机采样得到的。

（2）两阶段迭代更新

2.1 固定生成器更新判别器

判别器的目标：对真实图像赋较高的值，对生成的图像赋较低的值。

在此阶段中，生成器参数保持不变，只更新判别器，使其更好地区分真实数据（采样的真实数据）与生成数据（生成器生成的数据）。判别器的目标函数为：

更新过程通常使用梯度上升方法，通过多次迭代（例如5次更新）提高判别器的判别能力，但又不能使其达到完美状态，否则会导致生成器在下一阶段难以获得有效梯度。

判别器的具体目标即判别函数是：

 $V(G, D) = E_{x \sim p_{\text{data}}} [ \log(D(x)) ] + E_{\hat{x} \sim p_G} [ \log(1 - D(\hat{x})) ]$

其中，

$E_{x \sim p_{\text{data}}} [ \log(D(x)) ]$ ：判别器在采样后的真实数据集的评估指标。
$E_{\hat{x} \sim p_G} [ \log(1 - D(\hat{x})) ]$ ：其中的 $D(\hat{x})$ 为判别器对生成器生成数据给的分数，最大化 $E_{\hat{x} \sim p_G} [ \log(1 - D(\hat{x})) ]$ 表示最小化 $D(\hat{x})$ 。

判别器的训练的目标是最大化上述目标函数：

希望得到 $D^* = \arg \max_D V(D, G)$

2.2 固定判别器更新生成器

生成器的目标：生成与数据集更加相似的图像，使生成的图像在判别器中得到更高的分。

在这一阶段中，判别器参数固定，生成器根据判别器反馈进行参数更新。生成器的目标是“欺骗”固定的判别器。

生成器的具体目标是最小化生成图像与真实图像之间的相似度，即得到 $G^* = \arg \min_G \text{Div}(p_G, p_{\text{data}})$ ，这里的 $\text{Div}(p_G, p_{\text{data}})$ 用 $\max_D V(D, G)$ 表示，所以生成器的目标是更新 $G$ ，使得 $\max_D V(D, G)$ 最小，也就是让判别器判断的最差（但它仅从自身出发，即只改变 G）。

生成器的判别函数同样为：

 $V(G, D) = E_{x \sim p_{\text{data}}} [ \log(D(x)) ] + E_{\hat{x} \sim p_G} [ \log(1 - D(\hat{x})) ]$

生成器器的训练的目标是最小化上述目标函数：

希望得到 $G^* = \arg \max_G V(D^*, G)$

这里为什么要用 $D^*$ ？因为生成器和判别器是交替更新的（判别器5次，生成器一次，交替），一般可任务生成器的更新是在判别器之后的。

在更新 G 时，V(G, D)的第一项用不到，因为只有 $\hat{x}$ 是由 G 生成的。

3、GAN的目标函数与优化方法

（1）基于JS散度的目标函数及其公式

1.1 目标函数的基本表达式

GAN 的核心目标函数采用了最小最大博弈的形式，其公式为：

$\min_G \max_D V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}}\left[\log D(x)\right] +$ $\mathbb{E}_{\hat{x}\sim p_G}\left[\log \left(1-D\bigl(\hat{x}\bigr)\right)\right]$

其中：

$p_{\text{data}}$ 表示真实数据的分布；
$p_{\text{G}}$ 表示生成器生成的数据的分布；
$D(x)$ 是判别器对输入样本 $x$ 给出的真假概率；
$G(z)$ 则是生成器从随机向量 $z$ 生成的假样本。

也可以表示为：

$\min_G \max_D V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}}\left[\log D(x)\right] +$ $\mathbb{E}_{z\sim p_z}\left[\log \left(1-D\bigl(G(z)\bigr)\right)\right]$

其中： $p_z$ 表示生成器的参数；

$G(z)$ 则是生成器从随机向量 $z$ 生成的假样本。

1.2 判别器最优解与 JS 散度

更新判别式，解目标函数得到 $D^*$ ：

$V(G, D) = E_{x \sim p_{\text{data}}} \left[ \log(D(x)) \right] + E_{\hat{x} \sim p_G} \left[ \log(1 - D(\hat{x})) \right]$

$= \int_{x} p_{\text{data}}(x) \log(D(x)) dx + \int_{\hat{x}} p_G(\hat{x}) \log(1 - D(\hat{x})) d\hat{x}$

$= \int_{x} \left[ p_{\text{data}}(x) \log(D(x)) + p_G(x) \log(1 - D(x)) \right] dx$

当生成器 $G$ 固定时，求导令为 0 可极大化上式可得到最优判别器：

$D^*(x) = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_G(x)}$

其中 $p_G$ 为生成器生成的样本分布。
将最优判别器代入目标函数：

$V(G, D^*) = E_{x \sim p_{\text{data}}} \left[ \log(D^*(x)) \right] + E_{\hat{x} \sim p_G} \left[ \log(1 - D^*(\hat{x})) \right]$

$= E_{x \sim p_{\text{data}}} \left[ \log \left( \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_G(x)} \right) \right] + E_{\hat{x} \sim p_G} \left[ \log \left( \frac{p_G(\hat{x})}{p_{\text{data}}(\hat{x}) + p_G(\hat{x})} \right) \right]$

$= -2 \log 2 + \text{KL} \left( p_{\text{data}} \parallel \frac{p_{\text{data}} + p_G}{2} \right) + \text{KL} \left( p_G \parallel \frac{p_{\text{data}} + p_G}{2} \right)$

其中： $\text{KL} \left( p_{\text{data}} \parallel \frac{p_{\text{data}} + p_G}{2} \right) + \text{KL} \left( p_G \parallel \frac{p_{\text{data}} + p_G}{2} \right)$ 为 $p_{\text{data}}$ 和 $p_G$ 的JS散度。

JS散度的定义为：

$\text{JSD}(p \parallel q) = \frac{1}{2} \text{KL}(p \parallel \frac{p(x) + q(x)}{2}) + \frac{1}{2} \text{KL}(q \parallel \frac{p(x) + q(x)}{2})$

JS散度是KL散度的对称版本。
它的值域为 $[0, \log 2]$ ，其中 $\text{JSD}(p \parallel q) = 0$ 表示 $p$ 和 $q$ 完全相同， $\text{JSD}(p \parallel q) = \log 2$ 表示它们完全不同。

当 $p_G = p_{\text{data}}$ 时， $V(G^*, D^*) = -2 \log 2$ 。

这反映出 GAN 通过极小化目标函数，实际上是在缩小 $p_G$ 与 $p_{\text{data}}$ 之间的 JS 散度，从而使生成分布逐渐向真实数据分布靠拢。

（2）梯度消失与JS散度局限性分析

2.1 梯度消失问题

目标函数为：

$\min_G \max_D V(D, G) = \mathbb{E}_{x\sim p_{\text{data}}}\left[\log D(x)\right] +$ $\mathbb{E}_{z\sim p_z}\left[\log \left(1-D\bigl(G(z)\bigr)\right)\right]$

如果将判别器训练到最好，即 $D^{*}(x)=\sigma (x)$ ，图像如下图子图1，由于判别器很好，则生成的样本得分都是0，即生成的样本所在的位置如子图1中圈出的位置，也就是说 $D\bigl(G(z))$ 都等于0， $G(z)$ 的范围都在接近-10的位置。

则 $log(1-D^{*}(x))=log(1-\sigma (x))$ 的图如下子图2，

所以 $\frac{d}{d(G(z))}(\mathbb{E}_{z\sim p_z}\left[\log \left(1-D\bigl(G(z)\bigr)\right)\right])$ 关于 $G(z)$ 的图像如下图的子图4，而 $G(z)$ 的范围都在接近-10的位置，所以 $V(D^*,G)$ 关于 $G$ 就没有了梯度。从而 $V(D^*,G)$ 对 $G$ 的参数就没有了梯度，出现梯度消失。

梯度消失问题的解决

JS散度的梯度消失问题：判别完美将生成器样本归类为假样本，但生成器更新时收不到梯度。

改进：当判别器对生成样本充满信心判定生成样本时采用非饱和损失。

具体操作：

        由：

         $D^* = \max_D E_{x \sim p_{\text{data}}} \left[ \log(D(x)) \right] + E_{z \sim p_z} \left[ \log(1 - D(G(z))) \right]$

         $G^* = \min_G E_{z \sim p_z} \left[ \log(1 - D^{*}(G(z))) \right]$

        改为：

         $D^* = \max_D E_{x \sim p_{\text{data}}} \left[ \log(D(x)) \right] + E_{z \sim p_z} \left[ \log(1 - D(G(z))) \right]$

         $G^* =- \min_G E_{z \sim p_z} \left[ \log( D^{*}(G(z))) \right]$

         $= \max_G E_{z \sim p_z} \left[ \log(D^{*}(G(z))) \right]$

画出图像为：

虽然 $G(z)$ 的范围是在-10附近，但是那个地方有梯度，是-1

2.2 JS散度局限性

JS散度的第一个局限性就是上面介绍的梯度消失问题。

下面介绍另一个局限性：

当两个分布不重叠时，JS散度均为 log 2，不能带来更新梯度。如下图，只要两个分布不重叠，无论两个分布距离多远，JS散度都不变。所以就两个分布不重叠时就没梯度了。只有当两个分布相差很小时，JS散度才有意义

而且，许多现实世界数据集的维度只是看起来很高（如图像），但其实集中在低维流形中。对生成器而言，当给定小尺寸（如100）的输入噪声变量，要生成更大的图像（如64x64）时，这4096个像素上的颜色分布由小的100维随机数向量定义，很难填满整个高维空间。因为真实图像和生成器生成的图像都在低维流形中，它们肯定几乎是不相交的。也就是说，现实问题中，两个高维的分布几乎都是不相交的。

2.3 模式崩塌

GAN 的优化目标是一个 min-max 博弈，生成器的主要目标是使得生成的样本能够最大化欺骗判别器，而不是生成样本分布的多样性。因此，生成器可能找到一种简单的策略（例如只生成某一种样本）就能成功欺骗判别器，从而导致模式崩塌。

GAN 的优化过程是一个非凸博弈，生成器和判别器的损失函数在训练过程中相互依赖。这种博弈关系容易导致梯度更新不稳定，如判别器可能过于宽松，导致生成器学会仅生成少量模式就能骗过判别器。

判别器过强，梯度消失，生成器停止学习，容易引发生成器倾向于专注于生成少数模式，而非覆盖整个数据分布。

当两者分布之间的重叠区域很小时，JS 散度不具有指导意义，导致生成器难以获得有效的梯度更新。

4、Wasserstein距离与WGAN

（1）Wasserstein距离的直观解释与定义

直观解释
Wasserstein 距离又称“推土距离”（Earth Mover’s Distance），其直观意义在于：
- 想象有两堆“土堆”，其中一堆代表真实数据分布，另一堆代表生成数据分布。
- Wasserstein 距离即为将一堆“土”重新搬运成另一堆“土”所需的最小运输成本，其中运输成本通常与搬运的距离成正比。
  这种解释突出了 Wasserstein 距离对分布“差异”的几何度量，相较于传统的散度（如 JS 散度），在衡量不重叠或分布支持集几乎无交集的情形下能提供更平滑、有效的梯度信息。

正式定义
对于两个概率分布 $p$ （真实数据分布）和 $q$ （生成数据分布），Wasserstein 距离定义为：
$W(p, q) = \inf_{\gamma \in \Pi(p, q)} \int_{x \times y} c(x, y) d\gamma(x, y)$
其中， $\Pi(p, q)$ 表示所有满足边缘分布分别为 $p$ 和 $q$ 的联合分布集合。这个公式反映了在所有可能的 “ 运输方案 ” 中，选择运输成本最小的方案作为两分布间的距离。
Wasserstein 距离在 GAN 训练中能够提供更稳定的梯度信息。求解最优传输问题，涉及联合 $\gamma$ 的优化：在所有可能的联合分布 $\gamma$ 中，inf寻找总代价最小的 $\gamma$ 。

（2）1维Wasserstein距离计算及离散、连续情况

1维情况下的计算
在一维空间中，Wasserstein 距离可以通过比较累积分布函数（CDF）的差异来计算。对于累积分布函数 $F_p$ 和 $F_q$ ，1维 Wasserstein 距离为：
$W(p_r, p_g) = \int_{-\infty}^{+\infty} |F_r(x) - F_g(x)| \, dx$
这种积分形式直观地反映了两个分布在各个位置上的累计差异。

离散情况
当数据为离散形式（例如离散采样的点），可以将分布看作由 Dirac 函数构成的集合，此时 Wasserstein 距离通常通过排序样本后计算两组样本对应位置的距离之和来估计。
连续情况
对于连续分布，上述积分形式就是严格意义下的计算方法，需要对整个实数域上的累积分布函数进行积分，反映了连续空间中分布的整体差异。
文档中通过具体例子展示了如何在一维情形下，从离散数据和连续分布两个角度计算 Wasserstein 距离，以帮助理解这一度量在不同数据情形下的应用。

Wasserstein 距离和JS散度的比较：（当 p 、q 为两个 $\delta$ 函数时的JS散度）

（3）Kantorovich-Rubinstein对偶性与1-Lipschitz约束

Wasserstein 距离是求最优联合分布，不易计算，转化为对偶问题。

Kantorovich-Rubinstein 对偶性
Wasserstein 距离的对偶表达，即：

$W(p_r, p_g) = \underset{f\epsilon 1-Lipschitz}{\sup} \left( \mathbb{E}_{x\sim p_{data}}[f(x)] - \mathbb{E}_{x\sim p_G}[f(x)] \right)$

这里的 $f\epsilon 1-Lipschitz$ 表明，f 是一个 1-Lipschitz 条件的函数，也就是说， $f$ 在任一点的梯度小于等于1，即有：

$|f(x_1) - f(x_2)| \le \|x_1 - x_2\|$

这一对偶性说明，Wasserstein 距离可以通过寻找一个“最佳判别函数”（在 GAN 中称为“critic”）来近似计算。文档中对这一理论基础做了详细论述，强调了对偶表达式在 WGAN 设计中的重要作用。

K-Lipschitz 连续性：

$|f(x) - f(y)| \leq K |x - y|$

梯度有界：

$\frac{|f(x) - f(y)|}{|x - y|} \leq K$

1-Lipschitz 约束的重要性
为了保证对偶表达式的成立，critic 必须满足 1-Lipschitz 条件。实践中常通过以下方式来实现这一约束：

权重裁剪：直接对网络参数进行限制，使其在一个固定区间内变化；
梯度惩罚：通过在损失函数中增加一项，对梯度进行约束，确保在采样点处梯度接近 1。
这两种方法都是为了确保 critic 不会因为过于陡峭或平滑而破坏对偶性的成立，从而影响 Wasserstein 距离的准确计算和梯度传递。
这个约束其实本质还是王木头所讲的为模型加入先验，让模型不至于完全服务于数据集，保证了模型靠近自然的能力。

（4）WGAN的目标函数及 WGAN的优势

4.1 目标函数设计

在 WGAN 中，目标函数不再直接采用原始 GAN 中基于交叉熵的形式，而是基于 Wasserstein 距离的对偶表达式构造。其目标函数为：

$\min_G \max_{D\in \mathcal{D}} \; (\mathbb{E}_{x\sim p_{\text{data}}}[D(x)] - \mathbb{E}_{z\sim p_z}[D(G(z))])$

其中， $\mathcal{D}$ 表示所有满足 1-Lipschitz 条件的函数集合（即 critic 的函数空间）。这一目标函数直观上即为对 Wasserstein 距离的近似估计，生成器 $G$ 试图最小化真实分布与生成分布之间的 Wasserstein 距离，而 critic 则努力最大化这一差值。

如果不对 D 进行限制，则模型不会收敛，即 $D(x)$ 会被拉到正无穷，而 $D(G(z))$ 会被拉到负无穷。而对 D 进行限制后，D 会平滑得分开 $p_{data}$ 和 $p_G$ ，如下图：

4.2 对 D 平滑性限制得实现方式

早期，对D平滑性限制是算梯度的时候进行截断，最大只能是1 。后来进行了改进，在普空间中进行限制，即 Spectral Normalization → 使得函数在每个地方的梯度的模小于等于1。

4.3 WGAN的优势

相比传统 GAN，WGAN 在训练上有多项改进：

稳定性提升：由于 Wasserstein 距离提供了全局平滑的梯度，即使真实分布和生成分布支持集没有重叠，也能获得有意义的梯度信息，从而缓解了梯度消失问题。
缓解模式崩溃：WGAN 的目标函数能更直接地反映分布间的距离，减少生成器陷入模式崩溃（mode collapse）的风险。
critic 的多次更新：实践中通常采用多步更新 critic（例如每更新生成器前 critic 更新多次），以确保 critic 能够充分学习到分布间的差异，从而为生成器提供更稳定的梯度。
文档中详细阐述了这些训练改进策略，并通过数学公式和实验图示证明了 WGAN 相对于传统 GAN 的优越性。

4.4 WGAN小节

原始 GAN:
$\underset{G}{\min} \underset{D}{\max} E_{x \sim p_{\text{data}}} \left[ \log(D(x)) \right] + E_{z \sim p_z} \left[ \log(1 - D(G(z))) \right]$
WGAN:
$\underset{G}{\min} \underset{D\epsilon 1-Lipschitz}{\max} E_{x \sim p_{\text{data}}} \left[ D(x) \right] - E_{z \sim p_z} \left[ D(G(z)) \right]$

从数学的角度：JS散度 $\rightarrow$ Wasserstein距离

从工程的角度：

去掉 log
Lipschitz平滑

5、现象 GAN的扩展与融合模型

（1）作为外挂的GAN：VAE+GAN、Flow+GAN、Diffusion+GAN

基本思想
这类模型将 GAN 的对抗训练作为一个外挂或附加模块，结合其他生成模型（如 VAE、Flow 模型、扩散模型）的优势。通过在原有生成模型的基础上添加一个对抗损失，使得生成结果不仅满足重构或概率建模要求，同时更具真实感。

实际操作

对其他生成模型的生成结果，增加一个额外的损失：生成的结果是否足够“真实”。

VAE+GAN
- 重构与对抗损失结合：传统 VAE 在生成时主要依赖重构损失（reconstruction loss）和 KL 散度来优化，往往会导致生成图像模糊。VAE+GAN 在 VAE 的基础上增加了对抗损失，让生成器（通常与 VAE 的解码器共享结构）不仅要最小化重构误差，还要“欺骗”判别器，使生成图像看起来更加真实。
- 网络协同：编码器将输入图像映射到潜在空间，再经过生成器生成图像；同时判别器判断生成图像是否真实，从而引入“重构对抗”机制。

重构损失是一个很强的损失，训练时不会不稳定，也不会造成模式坍塌等。

对抗损失比较灵活，自由度高，训练时容易不稳定，容易造成模式坍塌。

Flow+GAN 与 Diffusion+GAN
- Flow 模型与扩散模型本身可以对数据进行精细建模，但在一些场景下生成图像的细节或真实感仍不足。将 GAN 捆绑为外挂，可以对生成结果施加一个额外的“真实性”约束。
- 外部损失设计：在这类架构中，GAN 的损失项被附加在基础模型的损失上，即“n重构损失 + 对抗损失”，促使生成器输出的图像在保持原有结构或概率密度特性的同时，进一步提升细节与真实感。

总体来看，“X+GAN”策略利用对抗训练补充其他模型的不足，使得生成结果在视觉质量上获得明显改善。

（2）条件GAN（Conditional GAN）

2.1 条件输入（如标签、文本）对生成器的影响

条件 GAN 通过在生成器和判别器中引入条件变量（如标签、文本、声音等），实现更具控制性的生成。主要包括以下两个方面：

条件信息嵌入
- 在条件 GAN 中，生成器不仅接受随机噪声作为输入，还同时输入条件信息，如类别标签或描述性文本。
- 条件信息可以通过嵌入向量、拼接或其他方式融合到生成器中，从而指导生成过程，使得生成图像在特定属性上满足条件要求（例如“红眼、黑发”或“red hair, green eyes”）。
生成器的调控作用
- 当条件信息明确且正确融合时，生成器会根据输入条件生成符合预期特征的图像；
- 但也有提示生成器有时可能忽略条件输入，若条件信息未充分发挥作用，则生成器可能只关注提升图像的真实度而忽略条件匹配。

2.2 判别器同时判断真实度与条件匹配性

双重判别任务
- 条件 GAN 的判别器不仅要判断图像是真实图像还是伪造图像，还需判断图像是否与给定的条件相匹配。
- 这种设计通常通过扩展判别器的输出，使其同时输出一个真实性评分和一个条件匹配评分（例如判断图像中的属性是否与文本描述一致）。
监督信号强化
- 判别器对条件匹配性的判断为生成器提供了更细致的反馈，促使生成器在生成真实感的同时，也更关注条件信息的准确反映。
- 文档中展示了不同示例（如文本描述与图像配对），说明了在训练过程中，正确的条件匹配对于生成器学习目标的重要性。
判别器如果不对条件进行匹配
- 由于判别器的输出要反馈给生成器进行生成器的更新，如果判别器不对条件进行匹配，生成器中的对于条件的信息就会逐渐削减，慢慢没有了条件的影响。

这种同时对图像真实性和条件匹配性的判断机制，使得条件 GAN 在很多应用中（如图像生成、文本到图像转换等）表现出更好的定向生成能力。

（3）Cycle GAN 与图像翻译

图像翻译任务旨在将一种图像风格或域映射到另一种图像风格或域，Cycle GAN 是其中的代表性方法，尤其适用于无配对数据场景。

无配对指的是图像原域与图像映射域没有一一对应。

3.1 无配对数据下的映射学习

挑战与需求

在很多实际应用中，很难获得成对的图像数据（例如白天与夜晚、夏季与冬季场景等），这就需要在无配对数据条件下学习不同域之间的映射关系。
Cycle GAN 正是为了解决这一问题而设计，它可以在没有成对数据的情况下，学习从一个域到另一个域的转换。

非Cycle GAN的情况

对于下图问题，将真实图像转化为相应的二次元图像：

应该在第一个图中的二次元图像（男）有更强的匹配，而第二幅图中的二次元图像（女）有更小的匹配度。但如果不采用Cycle GAN，匹配成女的二次元图像可能也有很高的匹配度。

因此可使用如下形式的Cycle GAN：

映射学习过程

通过两个生成器分别实现双向映射，即从域 A 到域 B，再从域 B 回到域 A；
每个生成器均由对应的判别器监督，使得生成的图像在目标域中具备较高的真实感。

3.2 Cycle一致性约束的引入与作用

循环一致性损失

为了确保映射学习过程中不丢失原始信息，引入了 Cycle 一致性约束。
具体地，若将图像从域 A 映射到域 B 后，再映射回域 A，则生成的图像应与原始图像尽可能接近。
这一约束可以通过以下形式的损失表达： $L_{\text{cyc}} = \mathbb{E}_{x \sim p_A}\left[\|F(G(x)) - x\|\right] + \mathbb{E}_{y \sim p_B}\left[\|G(F(y)) - y\|\right]$ 其中 $G$ 表示 A→B 的映射， $F$ 表示 B→A 的映射。

作用与效果

Cycle 一致性有效避免了生成器完全偏离输入内容的情况，确保在风格转换过程中保留关键的结构信息。
文档中通过图示说明了映射流程和一致性约束的作用，展示了在无配对数据条件下如何成功实现图像翻译。
下图展现了Cycle GAN在两个域中相互转化的流程图。

（4）其他相关变体：Dual GAN、Disco GAN、StarGAN

Dual GAN
- 主要用于无监督的图像到图像翻译任务，通过双向生成网络实现映射学习，其核心思想与 Cycle GAN 类似，但在网络结构和损失设计上有所不同。
Disco GAN
- 侧重于跨域映射的发现，尤其是用来捕捉两个域之间隐含的对应关系。
- 它在设计上注重保持不同域之间的语义一致性，从而实现更好的风格迁移和属性转换。
StarGAN
- 旨在实现多域图像翻译，通过一个统一的生成器和判别器模型，能够同时处理多个域之间的转换任务。
- 相比于传统的双域映射，StarGAN 在多域场景下具有更高的灵活性和效率，适用于复杂的图像转换需求。

这些变体均是在基本 GAN 框架上，通过设计不同的网络结构和损失函数，以应对各种特殊应用场景和数据分布问题，扩展了 GAN 的应用范围。

四、扩散模型（DDPM）

全称为：Denoising Diffusion Probabilistic Models

1、扩散模型基本原理

（1）扩散模型：渐变生成

生成思想：图像的生成过程是一个由高噪声状态逐步“雕刻”出干净图像的过程，强调“渐进式”与“逐步去噪”的思路。如下图所示：

（2）为什么从噪声生成图像可行？

理论依据：扩散模型通过精心设计的正向加噪过程，建立了噪声与图像之间的映射关系。在反向过程中，只要能够准确预测并去除这些噪声，原始图像的信息就能够被恢复出来。
关键步骤：生成的核心不在于直接从零开始构造图像，而在于如何精确地“去除”噪声，从而显露出图像内在的结构与细节。整个过程类似于从一块大石头开始的雕塑，一步一步去除无用的东西。
生成图像的关键是去噪。

（3）核心模块：噪声预测器

去噪模块Denoise中最关键的就是噪声预测器。去噪模块构造如下图所示：

噪声预测器：在去噪过程中，负责预测当前噪声分布。

核心功能：噪声预测器通过学习如何从噪声图像中估计出被加入的噪声量，从而在反向过程中通过“移除”这些噪声逐步恢复图像。
模型设计：通常采用神经网络（如UNet）作为噪声预测器，通过大量样本训练，使其能够在不同噪声水平下准确估计噪声信息。
生成效果：预测器的准确性直接决定了去噪效果和最终生成图像的质量，因此其设计与训练成为扩散模型的关键难点之一。

（4）训练噪声预测器

4.1 训练思想

如图，噪声预测器的输入为红色圈出的，输出为蓝色圈出的。我们只需通过很多 “ 输入-输出 ” 对即可完成对噪声预测器的训练，这个噪声预测器是否是 “ 好的 ” 的前提是输出图像减去它输出的结果会使得输入图像变清晰。

训练噪声预测器的训练样本：可人为构造。

目标函数可以是：噪声的重构误差（L2损失）

4.2 构造噪声预测器的训练样本

噪声预测器的训练样本即为：很多 “ 输入-输出 ” 对，通过前向加噪产生。如下图所示：

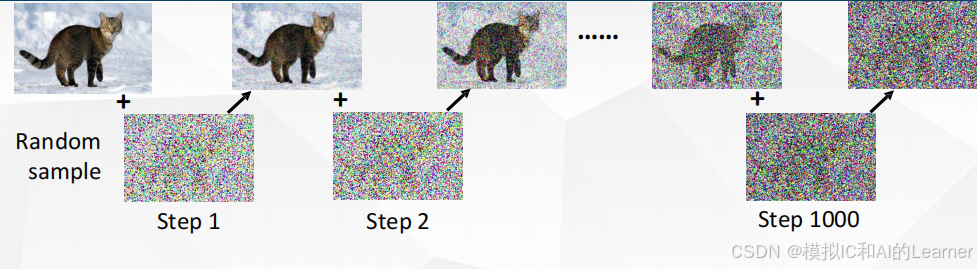
而噪声预测器的 “ 输入-输出 ” 对样本为：

2、DDPM 算法

（1）DDPM的训练算法

DDPM 的训练过程主要由两大模块构成：前向扩散过程（目的：获得噪声预测器的训练样本） 和 噪声预测器的训练，终极目标就是训练得到一个好的噪声预测器。

训练步骤总结：
1. 从数据集中采样干净图像 $x_0$ 。
2. 随机采样时间步 $t$ （通常均匀分布于1至T）。
3. 采样噪声 $\epsilon$ ，生成带噪声图像 $x_t$ 。
4. 将 $x_t$ 和 $t$ 输入到噪声预测器，得到预测噪声。
5. 计算 L2 损失，反向传播更新网络参数。

1.1 前向扩散过程

目标与过程：
从一个干净图像 $x_0$ 出发，通过多步加噪声过程将其逐渐转变为近似纯噪声的图像。
- 每一步都会向图像中加入一小部分高斯噪声。
- 经过多次噪声叠加后，最终得到的 $x_t$ 可以看作是由原始图像和多次独立加入的高斯噪声的线性组合（利用了两个正态分布之和仍为正态分布的性质），可等价于只加入了一次噪声。
数学表达式：
文档给出了类似如下的公式（格式略有简化）：

其中：
- 这个式子表明，添加 t 次噪声后的图像可一次计算出来。
- $\bar{\alpha}_t$ 为累计保持原始信息的比例（与噪声调度有关），下面 1.3 有关于 $\bar{\alpha}_t$ 的详解。
- 表示每一步采样的标准高斯噪声。

1.2 噪声预测器与损失函数

噪声预测器：
训练目标是利用一个参数化的神经网络（通常基于 U-Net 架构）来预测在某一噪声水平下加入的噪声，记作 $\epsilon_\theta(x_t, t)$ 。
- 网络接收带噪声的图像 $x_t$ 以及当前时间步 $t$ 作为输入，输出对噪声的预测。
训练目标与损失函数：
采用 L2 损失函数，比较预测噪声与实际添加的噪声：
- 这种损失函数通过重参数化技巧简化了问题，使模型直接学会如何从噪声图像中恢复出原始图像的信息。
- 文档中通过多次加噪声与一次加噪声之间的数学推导，验证了前向过程的合理性和生成过程中噪声合成的正态性。

通过这种训练，模型逐步学会了如何在不同噪声水平下精确估计噪声，为后续的反向生成过程提供了可靠基础。

1.3 多次添加噪声等价于一次添加噪声详细解析

如下图，由于高斯分布的性质，多次加噪声可以通过一次加噪声实现。

推导过程：

由高斯分布的性质：两个正态分布的和仍然是正态分布，即

$N(0, \sigma_1^2 I) + N(0, \sigma_2^2 I) = N(0, \sigma_1^2 + \sigma_2^2 I)$

得总的噪声得方差系数为

$(1 - \beta_2) \beta_1 + \beta_2 = \left( \sqrt{\beta_1 + \beta_2 - \beta_1 \beta_2} \right)^2 = \left( \sqrt{1 - (1 - \beta_2)(1 - \beta_1)} \right)^2$

即

$x_2=\sqrt{(1-\beta _1)}\sqrt{(1-\beta _2)}\cdot x_0 + \sqrt{1-(1-\beta _1)(1-\beta _2)}\cdot \epsilon$

扩展一下

$x_t=\sqrt{(1-\beta _1)}\cdot \cdot \cdot \sqrt{(1-\beta _t)}\cdot x_0 + \sqrt{1-(1-\beta _1)\cdot \cdot \cdot (1-\beta _t)}\cdot \epsilon$

令 $\alpha _{t}=1-\beta _{t}$ ， $\bar{\alpha _{t}}=\prod_{i=1}^{t}\alpha _{i}$ ，则上式可写为

$x_t=\sqrt{\bar{\alpha _{t}}}\cdot x_0+\sqrt{1-\bar{\alpha _{t}}}\cdot\epsilon$

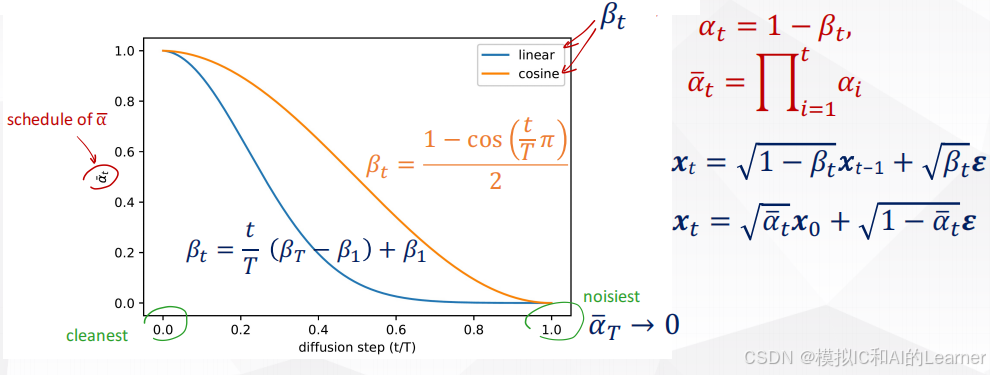
其中， $\beta _{t}$ 取值由噪声调度决定：

噪声调度（Noise Schedule）：
噪声系数的设置，指出当 $t$ 较小时，图像与原图接近，因而需要较小的噪声方差；而 $t$ 较大时，图像接近纯噪声，可以采用较大的噪声方差。

这一调度确保前向过程中的每一步均保持数学上的可逆性，为后续的生成提供理论基础。

两张图片非常接近时，用欧几里得距离才有意义。

当 $t$ 比较小时， $x_t$ 接近真实图片，要缩小 $x_{t-1}$ 与 $x_t$ 的差距，用较小的 $\beta_t$ ；
当 $t$ 比较大时， $x_t$ 比较接近噪声，噪声用欧几里得距离无妨，可以用较大的 $\beta_t$ 。

（2）DDPM的生成算法

DDPM 的生成过程即为反向扩散过程，它通过逐步去噪将纯噪声还原为真实图像。过程框图如下：

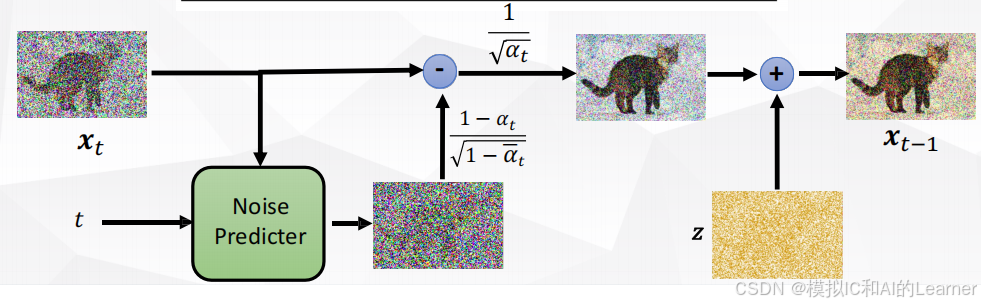
2.1 反向生成过程（Reverse Process）

初始状态：
生成过程从一个纯高斯噪声图像 $x_T \sim \mathcal{N}(0,I)$ 开始。
逆转噪声添加：
利用训练好的噪声预测器，逐步逆转前向过程中的噪声添加，每一步将 $x_t$ 转换为 $x_{t-1}$ ：
- 反向过程可以表示为： $\mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(x_t,t)\right)$ 然后，从均值为 $\mu_\theta(x_t,t)$ 且方差 $\sigma_t^2$ 的高斯分布中采样得到 $x_{t-1}$ 。
- 参数 $\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}$ 与前向扩散的系数有关，下面 2.3 有详细的分析。
- 这里， $\beta_t$ 和 $\sigma_t^2$ 的具体取值与噪声调度紧密相关，当 $t$ 较小时应采用较小的方差，而 $t$ 较大时方差可以较大，从而平滑地过渡到干净图像。

2.2 生成过程的关键步骤

迭代去噪：
生成过程以迭代方式进行，从 $t=T$ 开始，依次递减时间步：
1. 对于当前时间步 $t$ ，使用噪声预测器 $\epsilon_\theta(x_t,t)$ 得到噪声估计。
2. 根据预测噪声及当前噪声调度参数计算均值 $\mu_\theta(x_t,t)$ ；
3. 从 $\mathcal{N}(\mu_\theta(x_t,t), \sigma_t^2 I)$ 中采样，得到 $x_{t-1}$ ；
4. 重复上述过程直至 $t=0$ ，此时 $x_0$ 为最终生成的图像。
数学一致性与概率匹配：
反向生成过程与前向噪声添加过程在概率分布上严格对应，保证了整个生成链条的数学一致性。
- 下面 2.3 通过对“后向去噪过程”与“前向加噪声过程”的详细推导，证明了利用噪声预测器预测的噪声与前向过程中噪声的分布匹配，从而确保反向采样过程能够有效恢复出原始图像。
生成效果与计算代价：
虽然反向过程通常需要数百步迭代才能完成，但这种逐步去噪的策略能够保证生成图像的细节与稳定性。
- 每一步通过精细控制噪声去除，逐步提取出图像中的结构信息，使得生成结果远超直接映射的方法。

2.3 后向去噪与前向加噪的统一

实现“后向去噪过程”与“前向加噪声过程”的匹配是通过严格使前向加噪 $x_t = \sqrt{\bar{\alpha}_t}\, x_0 + \sqrt{1-\bar{\alpha}_t}\, \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)$ 的系数和后向去噪 $\mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}} \left(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(x_t,t)\right)$ 的系数在数学上严格统一来建立的。《通过前向的系数来推导后向的系数的详细推导过程见附录1 》

3、从VAE角度看扩散模型

（1）基本思路

VAE基本框架：
在传统的VAE中，我们引入隐变量 $z$ 来解释数据 $x$ ，目标是最大化数据的对数似然

$\ln p(x) = \ln \int p(x \mid z)\,p(z)\,dz$

由于直接计算困难，引入变分分布 $q(z\mid x)$ 并利用ELBO（变分下界）：

$\ln p(x) \geq \mathbb{E}_{q(z\mid x)}[\ln p(x\mid z)] - \mathrm{KL}(q(z\mid x) \parallel p(z))$

扩散模型的视角：
扩散模型（如DDPM）可以看作是一个逐步构建的VAE，其中数据生成过程被分解为多个小步骤。

这里， $x_1, \dots, x_T$ 充当了VAE中多个隐变量的角色，而前向过程的条件分布 $q(x_{1:T}\mid x_0)$ 就类似于编码器，后向过程的条件分布 $p_\theta(x_{0:T})$ 则类似于解码器。

编码器（前向过程）：
利用一系列小步的高斯噪声添加，将干净图像 $x_0$ 转化为一系列噪声图像 $x_1, x_2, \dots, x_T$ 。
解码器（后向过程）：
则从噪声 $x_T$ 开始，逐步去除噪声，恢复出 $x_0$ 。

（2）数学推导与ELBO分解

2.1 分解对数似然下界

对于数据 $x_0$ ，我们希望计算其对数似然 $\ln p_\theta(x_0)$ 。利用一系列中间状态 $x_1, \dots, x_T$ ，可写为：

$\ln p_\theta(x_0) = \ln \int p_\theta(x_{0:T})\,dx_{1:T}$

由于积分难以直接计算，采用变分方法，构造下界（VLB）：

$\ln p_\theta(x_0) \geq \mathbb{E}_{q(x_{1:T}\mid x_0)}\left[\ln \frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)}\right] = \mathcal{L}_{\text{VLB}}$

在扩散模型中，前向过程 $q(x_{1:T}\mid x_0)$ 是已知的，其每一步都采用简单的高斯分布：

$q(x_t\mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{\alpha_t}\,x_{t-1},\,\beta_t I)$

并且通过递归，可以得到

$q(x_t \mid x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}\,x_0,\, (1-\bar{\alpha}_t) I)$

其中 $\bar{\alpha}_t = \prod_{s=1}^t \alpha_s$ 。

2.2 下界的具体分解

利用变分推导，可以将下界分解为多个时间步的KL散度项和一个初始项。形式上（略去部分细节），下界可以写为：

$\mathcal{L}_{\text{VLB}} = \mathbb{E}_{q(x_{1:T}\mid x_0)}\Bigl[ -\ln p_\theta(x_0\mid x_1) -$

$\sum_{t=2}^T \mathrm{KL}\Bigl(q(x_{t-1}\mid x_t,x_0) \parallel p_\theta(x_{t-1}\mid x_t)\Bigr) -\mathrm{KL}\Bigl(q(x_T\mid x_0) \parallel p(x_T)\Bigr) \Bigr]$

其中各项的意义为：

重构项 $-\ln p_\theta(x_0\mid x_1)$ ：
对应于解码器从第一步噪声恢复出原始图像的能力，相当于VAE中的重构误差。
中间步骤的KL项：
每一步都衡量模型在后向过程 $p_\theta(x_{t-1}\mid x_t)$ 与真实后验 $q(x_{t-1}\mid x_t,x_0)$ 之间的差距。
最后一步的KL项：
保证最末状态 $x_T$ 与先验 $p(x_T)$ （通常取为标准正态分布）匹配。

由于前向过程的每一步都是简单的高斯分布，上述KL项均可以解析计算。这种分解使得整体目标变成对多个简单KL项和一个重构项的求和，与VAE的ELBO形式非常相似。

（3）参数化与噪声预测

3.1 引入噪声预测器

在生成（后向）过程中，直接利用 $q(x_{t-1}\mid x_t,x_0)$ 的形式是不可能的，因为 $x_0$ 在生成时是未知的。解决方法是引入参数化模型 $\epsilon_\theta(x_t,t)$ 来预测噪声，并将 $x_0$ 用 $x_t$ 和预测噪声表示：

$x_0 \approx \frac{1}{\sqrt{\bar{\alpha}_t}}\Bigl(x_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon_\theta(x_t,t)\Bigr)$

3.2 后向分布的参数化

将上述表达式代入到后向分布 $q(x_{t-1}\mid x_t,x_0)$ 的均值中，可以得到参数化的后向均值：

$\mu_\theta(x_t,t) = \frac{1}{\sqrt{\alpha_t}}\Bigl(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_\theta(x_t,t)\Bigr)$

并令后向分布为：

$p_\theta(x_{t-1}\mid x_t) = \mathcal{N}\bigl(x_{t-1};\, \mu_\theta(x_t,t),\, \sigma_t^2 I\bigr)$

这样的设计使得整个模型在训练时通过最小化各步KL散度项来学习如何从噪声中恢复出原始图像，与VAE中的重构和先验匹配损失相似。

（4）对比VAE与扩散模型

局部近似与全局建模：
VAE在全局上对数据分布做建模，因采用单一步骤的高斯假设，可能难以捕捉数据的复杂结构；
而扩散模型将生成过程分解为多个小步骤，每一步只需建模微小变化，正如“在小范围内曲线可以近似为直线”，这种局部线性近似更易于准确拟合复杂分布。
多步建模的优势：
每一步都只需预测小幅噪声，因此网络可以更精细地调整生成过程；
同时，多步KL散度的累积实际上构成了对整体对数似然的下界优化，类似于VAE的ELBO，但由于步骤划分更细，模型的表达能力更强。

（5）总结

VAE视角下的扩散模型：
- 将数据生成过程分解为多个隐变量 $x_1,\dots,x_T$ 的状态转移，前向过程作为编码器，后向过程作为解码器。
- 与VAE类似，通过构造变分下界（ELBO）对整体对数似然进行优化。
数学分解与目标函数：
- 下界由重构项和多步KL散度项组成，每一步的KL项均可解析计算。
- 参数化的后向分布通过噪声预测器实现，使得生成过程仅依赖于当前状态 $x_t$ 的信息。
优势与改进：
- 由于每步变化较小，简单的高斯假设足以准确描述局部变化，从而使得扩散模型在捕捉复杂数据分布上较传统VAE更具优势。

这种用VAE思想解释扩散模型的方法，不仅揭示了两者在目标函数上的共性，还展示了扩散模型如何通过多步细粒度建模来克服传统VAE在全局建模上的不足，为生成高质量图像提供了理论基础和实践依据。

4、扩散模型的其他解读

除了从VAE的角度解释扩散模型外，还能从其他角度解释扩散模型：

基于能量的模型和分数匹配
自回归模型
SDE和ODE
标准化流程
循环神经网络
$\cdot \cdot \cdot \cdot \cdot$

5、其他解读—基于能量的模型和分数匹配（很重要，但有些还不太懂）

（1）能量模型视角

1.1 能量函数与概率分布

在能量模型（Energy-Based Model, EBM）中，我们通常将数据分布写为

$p(x) \propto \exp\bigl(-E(x)\bigr)$

其中 $E(x)$ 是能量函数。由此可知，数据的对数概率可以写为

$\ln p(x) = -E(x) - \ln Z$

这里 $Z$ 是归一化常数（配分函数）。
这种表示方式的一个优势在于，我们只需要关心能量函数的梯度（也就是分数函数），而不必直接计算难以获得的归一化常数。

1.2 分数函数与梯度

分数函数定义为数据分布对数密度的梯度

$s(x) = \nabla_x \ln p(x) = -\nabla_x E(x)$

由此可以看出，学习分数函数就等价于学习能量函数的负梯度。在扩散模型中，正是利用这一思想，通过对数据进行逐步噪声添加并构造对应的“扰动分布”，再用神经网络拟合这些扰动下的分数信息，从而达到建模复杂数据分布的目的。

（2）分数匹配（Score Matching）原理

2.1 传统分数匹配

原始的分数匹配方法由 Hyvärinen 提出，其目标是使模型预测的分数函数 $s_\theta(x)$ 与真实分数 $s(x)=\nabla_x \ln p(x)$ 尽可能接近。其损失函数形式为：

$\mathcal{L}_{\text{SM}} = \frac{1}{2}\,\mathbb{E}_{p_{\text{data}}(x)}\left[\left\|s_\theta(x) - \nabla_x \ln p_{\text{data}}(x)\right\|^2\right]$

然而，由于真实数据分布 $p_{\text{data}}(x)$ 的分数函数难以直接计算，这一目标难以直接优化。

2.2 去噪分数匹配

为了解决上述问题，Vincent 等人提出了去噪分数匹配（Denoising Score Matching, DSM）的策略。主要思想是在数据上添加一定幅度的高斯噪声，使得我们获得一个平滑的扰动分布

$q_\sigma(x) = \int p_{\text{data}}(x')\,\mathcal{N}(x; x',\sigma^2 I)dx'$

此时其分数函数可写为

$\nabla_x \ln q_\sigma(x) = -\frac{x - x'}{\sigma^2} \quad$ ，(近似关系)

实际训练时，我们采样原始数据 $x_0 \sim p_{\text{data}}(x)$ 并添加噪声得到

$x = x_0 + \sigma \epsilon, \quad \epsilon \sim \mathcal{N}(0,I)$

那么 DSM 的目标就是使网络预测的分数 $s_\theta(x, \sigma)$ 与 $-\frac{\epsilon}{\sigma}$ 接近，即最小化

$\mathcal{L}_{\text{DSM}} = \mathbb{E}_{x_0,\epsilon}\Bigl[\lambda(\sigma)\,\Bigl\|s_\theta(x_0+\sigma\epsilon,\sigma) + \frac{\epsilon}{\sigma}\Bigr\|^2\Bigr]$

其中 $\lambda(\sigma)$ 是针对不同噪声水平的权重因子。

（3）扩散模型中的能量模型与分数匹配

3.1 前向扩散过程与噪声添加

扩散模型中，我们定义一个前向过程，将干净数据 $x_0$ 逐步添加噪声，得到一系列变量 $x_1, x_2, \dots, x_T$ 。其中，每一步通常定义为：

$q(x_t \mid x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}\,x_{t-1},\,\beta_t I)$

经过多步迭代，可以证明 $x_t$ 与 $x_0$ 的关系为

$q(x_t \mid x_0) = \mathcal{N}\Bigl(x_t; \sqrt{\bar{\alpha}_t}\,x_0,\, (1-\bar{\alpha}_t) I\Bigr)$

其中 $\bar{\alpha}_t = \prod_{s=1}^t (1-\beta_s)$

3.2 逆过程与分数预测

在生成阶段，由于我们无法直接获得 $x_0$ ，需要从 $x_T$ 开始逐步还原到 $x_0$ 。逆过程可以写为

$p_\theta(x_{t-1}\mid x_t) = \mathcal{N}(x_{t-1};\, \mu_\theta(x_t,t),\, \Sigma_\theta(x_t,t))$

关键在于利用分数函数将 $x_0$ 表达为 $x_t$ 和噪声的函数。通过对 $q(x_t\mid x_0)$ 取对数求梯度，可以得到真实的分数：

$\nabla_{x_t} \ln q(x_t\mid x_0) = -\frac{1}{1-\bar{\alpha}_t}\Bigl(x_t - \sqrt{\bar{\alpha}_t}\,x_0\Bigr)$

这意味着，若能预测出这个梯度（或其负值），就能获得关于 $x_0$ 的信息。通常，我们引入一个参数化模型 $s_\theta(x_t,t)$ 逼近该分数，从而有：

$x_0 \approx \frac{1}{\sqrt{\bar{\alpha}_t}}\Bigl(x_t + (1-\bar{\alpha}_t)\,s_\theta(x_t,t)\Bigr)$

这样一来，利用分数匹配的目标函数，就能训练网络以精确预测不同噪声水平下的分数信息，从而在逆过程（生成过程中）指导数据的恢复。

3.3 目标函数的重新解释

实际上，可以证明扩散模型训练中针对每一步KL散度的优化，与加权的去噪分数匹配损失在数学上是等价的。具体地，每一项KL散度衡量的正是网络预测的分数与真实分数（由高斯扰动模型计算得到）之间的差异。通过对所有时间步求和，整个变分下界（ELBO）的优化目标就转化为一个多尺度、加权的分数匹配损失。

这种推导展示了两点核心思想：

局部近似：在每一个小噪声添加的步骤中，由于噪声幅度较小，数据分布在局部可以近似为高斯分布，从而使得分数函数可以精确计算。
多尺度分数匹配：通过在不同噪声水平下匹配分数，模型可以逐步“理解”数据的局部结构，并在生成阶段利用这一信息进行高质量采样。

（4）总结与思考

基于能量模型和分数匹配的角度，扩散模型的核心思想可以概括为：

能量模型：将数据分布表示为 $\exp(-E(x))$ ，重点在于学习能量函数（或其梯度，即分数函数），从而避免直接计算难以获得的归一化常数。
分数匹配：通过在不同噪声水平下使网络预测的分数函数接近真实（由高斯扰动计算的）分数，达到对数据分布的精确建模。去噪分数匹配的目标不仅易于计算，而且与扩散过程中的各步目标严格对应。
推导过程：从前向过程的噪声添加得到 $q(x_t\mid x_0)$ 的表达式，再计算其对数梯度，从而为逆过程提供理论依据。逆过程参数化中，利用分数预测重构 $x_0$ 的思想，使得整个采样过程等价于沿着数据分布的对数梯度进行“爬山”或“下降”。

这种解释不仅为扩散模型提供了一个直观的能量视角，也使得它与经典的分数匹配方法建立了联系，从而解释了为什么通过逐步去噪可以有效捕捉数据分布的复杂结构，以及为何该方法在生成高质量样本时表现出色。

6、GAN 和 Diffusion 比较

生成对抗网络（GAN） 和 扩散模型（Diffusion） 在生成方式、训练目标以及控制能力等方面有所不同：

GAN（生成对抗网络）：
- 生成速度：GANs 通常一次性生成样本，因此生成速度较快。
- 控制难度：由于生成器和判别器在对抗训练中博弈，控制生成内容变得较为复杂。
- 训练目标：GAN 使用对抗性训练，生成器通过最小化损失函数来骗过判别器。由于训练的不稳定性，可能会发生模式崩塌（mode collapse），即生成的样本质量多样性较差。
- 总结：GAN 在生成过程中速度较快，但在控制和稳定性方面存在挑战。
扩散模型（Diffusion Models）：
- 生成过程：扩散模型采用多步迭代的方式，逐步从噪声中恢复数据，因此生成速度较慢。
- 控制性：由于生成过程逐步进行，扩散模型的生成过程相对容易控制，且通常能够生成质量更高的样本。
- 训练目标：扩散模型使用一个简单的去噪目标，无需复杂的对抗训练。因此，扩散模型的训练相对稳定，通常不会发生模式崩塌。
- 总结：扩散模型虽然速度较慢，但生成过程的控制性较强，且训练更加稳定。

7、扩散模型在音频和自然语言领域的应用

扩散模型已被成功应用于多个领域，包括音频和自然语言生成：

扩散模型在音频生成中的应用：
- WaveGrad 是一种扩散模型，特别应用于音频生成。该模型通过反向扩散去噪过程逐步恢复音频信号的质量。
- 参考文献：WaveGrad，该模型能够生成更自然、更连贯的语音或音频内容。

扩散模型在文本生成中的应用：
- 挑战：由于文本是离散的，直接使用扩散模型进行文本生成存在困难。文本生成要求将离散的文字转换为潜在空间中的连续表示。
- 解决方案：通过在潜在空间上加入噪声，扩散模型可以有效地在文本的潜在表示空间中进行去噪和生成。研究如 DiffuSeq 和 DiffusER 提供了这种方法的优化与应用。

扩散模型在这些领域的应用表明它能生成高质量的音频和文本，但在文本生成时需要创新的处理方式来应对离散与连续数据的差异。

8、条件-扩散模型

条件扩散模型（Conditional Diffusion Models）是一类根据给定条件生成数据的扩散模型。与标准扩散模型不同，条件扩散模型能够在生成过程中引入外部信息（如标签、描述等）来引导生成过程。外部信息加入的位置是在训练噪声预测器时作为输入，如下图所示，常见的应用包括：

文本到图像生成：通过文本描述（如“一个骑马的宇航员”），条件扩散模型能够生成与描述相匹配的图像。
图像翻译：条件扩散模型可以根据输入图像的特征，生成与其风格或内容相符的输出图像。

这种类型的模型在现实世界应用中展现了强大的潜力，能够在多种场景下生成与特定条件匹配的高质量数据。

9、Stable Diffusion

Stable Diffusion 是一种广泛应用的扩散生成模型，特别在文本到图像生成方面具有显著优势。其特点和关键技术包括：

多步去噪过程：Stable Diffusion 通过多次迭代去噪生成图像，从而能够生成更高质量的图像。
文本到图像的桥梁：它能够将自然语言描述（如“一个在雪地里的猫”）转换为对应的图像。
U-Net架构：作为一种重要的图像生成结构，U-Net 在扩散过程中有着重要作用。它的编码-解码结构帮助模型从噪声中恢复清晰的图像。
自动编码器：Stable Diffusion 采用了自动编码器技术，有助于压缩图像数据并减少生成时的计算开销。
注意力机制：通过注意力机制，模型能够更加聚焦在图像的关键部分，从而提高生成图像的质量。

Stable Diffusion 在质量、控制性和多样性方面都表现出色，并在生成领域引领了新的趋势。

10、Diffusion Model推荐阅读材料

为了深入了解扩散模型的工作原理和应用，以下是一些推荐的阅读材料：

Perspectives on Diffusion Models：由 Sander Dieleman 提供的扩散模型深入分析，适合对模型原理有更深兴趣的读者。
生成扩散模型漫谈系列：这是一系列由苏剑林编写的中文资料，详细探讨了生成扩散模型的各个方面，适合中文读者。

这些资料能够帮助读者进一步理解扩散模型的理论背景及实际应用，增强对该领域的知识储备。

五、生成式模型评价

生成式模型的评价方法，特别是在图像生成任务中的应用。以下是一些关键点的总结：

自动化图像质量评估： 评估生成图像的质量时，采用了几种自动化方法，例如通过现成的图像分类器（如Inception网络、VGG等）来进行评估。这些分类器的输出可以反映图像的集中分布，这意味着生成的图像具有较高的视觉质量。
多样性和模式崩溃（Mode Collapse）： 生成的图像的多样性是评价的一个重要因素。模式崩溃（即生成器生成的图像过于单一）和模式丢失（即某些类别的图像无法被生成）的问题。通过对比真实数据和生成数据，研究者可以分析生成模型的多样性。
Inception Score（IS）与Fréchet Inception Distance（FID）：
- Inception Score (IS)：IS指标用于衡量图像的质量和多样性，IS值较大通常表示图像质量好且多样性大。
- Fréchet Inception Distance (FID)：FID用于度量生成图像和真实图像之间的分布差异，FID值越小，表示生成图像与真实图像越相似，质量越高

总体而言，生成式模型，可通过以上提出了几种可行的自动化评估手段和标准进行评价。

附录

1、后向去噪与前向加噪系数匹配的严格推导

（1）前向加噪过程的定义与推导

1.1 单步加噪过程

定义
前向过程从干净图像开始，每一步都加入少量高斯噪声，形式上定义为：其中：
- $\alpha_t = 1 - \beta_t$ 表示每一步保留原图信息的比例，
- $\beta_t$ 控制噪声的强度。

1.2 多步递推与闭式表达

递归关系
由于每一步的转换都是高斯分布，通过递归迭代，可以将 $x_t$ 与 $x_0$ 直接建立关系。利用高斯分布线性组合的性质，有：

$q(x_t \mid x_0) = \mathcal{N}\Bigl(x_t; \sqrt{\bar{\alpha}_t}\,x_0,\, (1-\bar{\alpha}_t) I\Bigr)$

其中：

$\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s$

表示经过 $t$ 步后，原始图像信息的累计保持率。

核心思想
这一推导利用了“两个正态分布之和仍为正态分布”的性质，使得前向过程从 $x_0$ 到 $x_t$ 的转换具有闭式表达，为后续逆过程的推导奠定基础。

（2）后向去噪过程的推导

2.1 目标与贝叶斯公式

目标
生成过程中，我们希望逆转前向过程，将纯噪声恢复成原始图像。具体来说，需要推导出：

$q(x_{t-1} \mid x_t, x_0)$

表示在已知当前状态 $x_t$ 以及原始图像 $x_0$ （训练时可利用，但生成时未知）的条件下，前一步 $x_{t-1}$ 的分布。

利用贝叶斯定理
根据贝叶斯公式，有：

$q(x_{t-1} \mid x_t, x_0) = \frac{q(x_t \mid x_{t-1})\,q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}$

由于上面三个条件分布都是高斯分布，故该条件分布依然为高斯分布，其均值和方差可以通过标准的条件高斯分布公式求得。

2.2 具体推导结果

均值与方差
经过详细推导，可以得到：

$q(x_{t-1} \mid x_t, x_0) = \mathcal{N}\Bigl(x_{t-1};\, \tilde{\mu}(x_t,x_0),\, \tilde{\beta}_t I\Bigr)$

其中均值 $\tilde{\mu}(x_t,x_0)$ 和方差 $\tilde{\beta}_t$ 分别为：

$\tilde{\mu}(x_t,x_0)= \frac{\sqrt{\bar{\alpha}_{t-1}}\,\beta_t}{1-\bar{\alpha}_t}\,x_0 + \frac{\sqrt{\alpha_t}\,(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\,x_t$

$\tilde{\beta}_t = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\,\beta_t$

这一推导依赖于已知前向过程 $q(x_t \mid x_0)$ 的闭式表达，以及高斯条件分布的性质。

（3）利用噪声预测器实现逆向生成

3.1 解决 $x_0$ 的未知问题

问题
在生成过程中， $x_0$ （原始图像）是未知的，因此直接使用上式中的 $x_0$ 计算均值不可行。

解决方案
引入参数化的噪声预测器 $\epsilon_\theta(x_t,t)$ ，利用前向过程的重参数化公式：

$x_t = \sqrt{\bar{\alpha}_t}\, x_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon,\quad \epsilon\sim\mathcal{N}(0,I)$

从中可以解出：

$x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}\Bigl(x_t - \sqrt{1-\bar{\alpha}_t}\,\epsilon\Bigr)$

3.2 参数化的后向均值

替换与重构
将 $x_0$ 的表达式代入先前 $\tilde{\mu}(x_t,x_0)$ 中，经过重构和化简，可以得到参数化的后向均值：

$\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}\Bigl(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_\theta(x_t,t)\Bigr)$

这一形式使得在生成过程中，只需利用当前的带噪图像 $x_t$ 和噪声预测器的输出，就可以计算出前一步 $x_{t-1}$ 的采样均值。

生成步骤
生成过程中从 $x_T \sim \mathcal{N}(0,I)$ 开始，逐步利用上述公式采样出 $x_{t-1}$ ，直至获得 $x_0$ （即生成的图像）。同时，后向过程的方差 $\tilde{\beta}_t$ 也可依据前向过程参数确定，从而确保采样的合理性。

（4）总结

整个推导过程可以总结为以下几点：

前向过程：
- 定义了一个逐步添加噪声的过程，使得 $x_t$ 可以表达为 $x_t = \sqrt{\bar{\alpha}_t}\, x_0 + \sqrt{1-\bar{\alpha}_t}\,\epsilon$ , 其中利用了多步高斯噪声叠加后的闭式表达。
后向过程：
- 利用贝叶斯定理，推导出在给定 $x_t$ 和 $x_0$ 条件下 $x_{t-1}$ 的分布，其均值为 $\tilde{\mu}(x_t,x_0)= \frac{\sqrt{\bar{\alpha}_{t-1}}\,\beta_t}{1-\bar{\alpha}_t}\,x_0 + \frac{\sqrt{\alpha_t}\,(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\,x_t$
噪声预测器的引入：
- 为了解决生成过程中 $x_0$ 的未知问题，利用重参数化技巧，将 $x_0$ 表达为 $x_t$ 与噪声的函数，并通过训练噪声预测器 $\epsilon_\theta(x_t,t)$ 来替代真实噪声，从而将后向均值写为： $\mu_\theta(x_t,t)=\frac{1}{\sqrt{\alpha_t}}\Bigl(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\,\epsilon_\theta(x_t,t)\Bigr)$