【机器学习chp10代码示例】降维

于 2025-03-05 20:26:36 发布
阅读量333 收藏 3
点赞数 3
分类专栏： 机器学习 文章标签： 机器学习 人工智能 降维 t-nse UMAP PCA 核化PCA
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_56997192/article/details/145970172
版权

目录

一、基于重构的降维

1、PCA

2、增量式PCA

3、核化PCA

二、基于全局结构保持的降维

1、多维缩放MDS

2、Isomap

三、基于局部结构保持的降维

1、LLE局部线性降维

2、拉普拉斯特征映射

3、t-NSE

4、UMAP

四、降维算法综合

1、降到二维

2、降到三维

一、基于重构的降维

1、PCA

# PCA对鸢尾花数据集降维

#!pip install plotly
import plotly.express as px
import pandas as pd
from sklearn import datasets
from sklearn.decomposition import PCA

# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 使用PCA降维到3个主成分
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)

# 创建DataFrame
df = pd.DataFrame(X_pca, columns=["PC1", "PC2", "PC3"])
df['species'] = y

# 使用plotly绘制3D散点图
fig = px.scatter_3d(df, x="PC1", y="PC2", z="PC3", color="species", title="3D PCA of Iris Dataset")
fig.show()

2、增量式PCA

# PCA和增量式PCA

# Authors: Kyle Kastner
# License: BSD 3 clause

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, IncrementalPCA

iris = load_iris()
X = iris.data
y = iris.target

n_components = 2
ipca = IncrementalPCA(n_components=n_components, batch_size=10)
X_ipca = ipca.fit_transform(X)

pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)

colors = ['navy', 'turquoise', 'darkorange']

for X_transformed, title in [(X_ipca, "Incremental PCA"), (X_pca, "PCA")]:
    plt.figure(figsize=(8, 8))
    for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
        plt.scatter(X_transformed[y == i, 0], X_transformed[y == i, 1],
                    color=color, lw=2, label=target_name)

    if "Incremental" in title:
        err = np.abs(np.abs(X_pca) - np.abs(X_ipca)).mean()
        plt.title(title + " of iris dataset\nMean absolute unsigned error "
                  "%.6f" % err)
    else:
        plt.title(title + " of iris dataset")
    plt.legend(loc="best", shadow=False, scatterpoints=1)
    plt.axis([-4, 4, -1.5, 1.5])

plt.show()

3、核化PCA

# 核化PCA降维

import numpy as np
import matplotlib.pyplot as plt

from sklearn.decomposition import PCA, KernelPCA
from sklearn.datasets import make_circles

np.random.seed(0)

X, y = make_circles(n_samples=400, factor=.3, noise=.05)

kpca = KernelPCA(kernel="rbf", fit_inverse_transform=True, gamma=10)
X_kpca = kpca.fit_transform(X)
X_back = kpca.inverse_transform(X_kpca)
pca = PCA()
X_pca = pca.fit_transform(X)

# Plot results

plt.figure()
plt.subplot(2, 2, 1, aspect='equal')
plt.title("Original space")
reds = y == 0
blues = y == 1

plt.scatter(X[reds, 0], X[reds, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X[blues, 0], X[blues, 1], c="blue",
            s=20, edgecolor='k')
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")

X1, X2 = np.meshgrid(np.linspace(-1.5, 1.5, 50), np.linspace(-1.5, 1.5, 50))
X_grid = np.array([np.ravel(X1), np.ravel(X2)]).T
# projection on the first principal component (in the phi space)
Z_grid = kpca.transform(X_grid)[:, 0].reshape(X1.shape)
plt.contour(X1, X2, Z_grid, colors='grey', linewidths=1, origin='lower')

plt.subplot(2, 2, 2, aspect='equal')
plt.scatter(X_pca[reds, 0], X_pca[reds, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_pca[blues, 0], X_pca[blues, 1], c="blue",
            s=20, edgecolor='k')
plt.title("Projection by PCA")
plt.xlabel("1st principal component")
plt.ylabel("2nd component")

plt.subplot(2, 2, 3, aspect='equal')
plt.scatter(X_kpca[reds, 0], X_kpca[reds, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_kpca[blues, 0], X_kpca[blues, 1], c="blue",
            s=20, edgecolor='k')
plt.title("Projection by KPCA")
plt.xlabel(r"1st principal component in space induced by $\phi$")
plt.ylabel("2nd component")

plt.subplot(2, 2, 4, aspect='equal')
plt.scatter(X_back[reds, 0], X_back[reds, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_back[blues, 0], X_back[blues, 1], c="blue",
            s=20, edgecolor='k')
plt.title("Original space after inverse transform")
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")

plt.tight_layout()
plt.show()

二、基于全局结构保持的降维

1、多维缩放MDS

# MDS降维

from sklearn.datasets import load_digits
from sklearn.manifold import MDS

import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = MDS(n_components=2)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()

2、Isomap

# Isomap降维

from sklearn.datasets import load_digits
from sklearn.manifold import Isomap

import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = Isomap(n_components=2)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()

三、基于局部结构保持的降维

1、LLE局部线性降维

# LLE局部线性降维

from sklearn.datasets import load_digits
from sklearn.manifold import LocallyLinearEmbedding

import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = LocallyLinearEmbedding(n_components=2)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()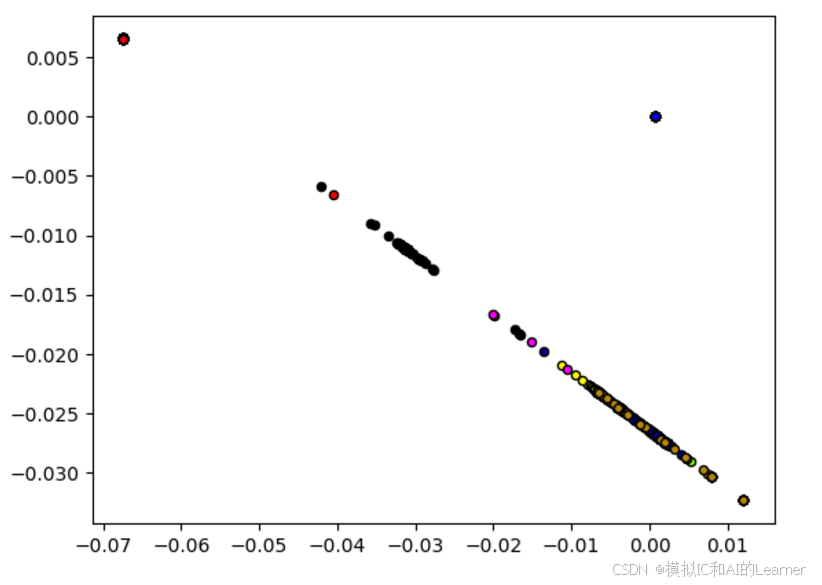

2、拉普拉斯特征映射

# 拉普拉斯特征映射-频谱降维

from sklearn.datasets import load_digits
from sklearn.manifold import SpectralEmbedding

import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = SpectralEmbedding(n_components=2)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()

3、t-NSE

# t-NES降维

from sklearn.datasets import load_digits
from sklearn.manifold import TSNE

import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = TSNE(n_components=2,init='pca',perplexity=30)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()

4、UMAP

# UMAP降维

!pip install umap-learn
from sklearn.datasets import load_digits
import umap
import numpy as np
import matplotlib.pyplot as plt

X, y = load_digits(return_X_y=True)
print(X.shape)

embedding = umap.UMAP(n_components=2, random_state=42)
X_transformed = embedding.fit_transform(X)
print(X_transformed.shape)
#画出来

digit_0 = y == 0
digit_1 = y == 1
digit_2 = y == 2
digit_3 = y == 3
digit_4 = y == 4
digit_5 = y == 5
digit_6 = y == 6
digit_7 = y == 7
digit_8 = y == 8
digit_9 = y == 9
plt.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
            s=20, edgecolor='k')
plt.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
            s=20, edgecolor='k')
plt.show()

四、降维算法综合

1、降到二维

# 降维综合--降到二维

import numpy as np
import matplotlib.pyplot as plt

# 导入各个模型
from sklearn.decomposition import PCA
from sklearn.decomposition import IncrementalPCA
from sklearn.decomposition import KernelPCA
from sklearn.manifold import MDS
from sklearn.manifold import Isomap
from sklearn.manifold import LocallyLinearEmbedding
from sklearn.manifold import SpectralEmbedding
from sklearn.manifold import TSNE
!pip install umap-learn
import umap

# 导入数据集
from sklearn.datasets import load_iris
from sklearn.datasets import make_circles
from sklearn.datasets import load_digits

# 模型名字
names = ["PCA","IPCA","KPCA","MDS","Isomap","LLE","SE","T-SNE","UMAP"]

# 模型初始化
JiangWei_models = [
    PCA(n_components=2),
    IncrementalPCA(n_components=2, batch_size=10), 
    KernelPCA(n_components=2, kernel="rbf", fit_inverse_transform=True, gamma=10),
    MDS(n_components=2),
    Isomap(n_components=2),
    LocallyLinearEmbedding(n_components=2),
    SpectralEmbedding(n_components=2),
    TSNE(n_components=2,init='pca',perplexity=30),
    umap.UMAP(n_components=2, random_state=42)
    ]

# 建立并整理数据集

iris = load_iris()
X_iris = iris.data
y_iris = iris.target
X_circles, y_circles = make_circles(n_samples=400, factor=.3, noise=.05)
X_digits, y_digits = load_digits(return_X_y=True)

datasets = [[X_iris,y_iris],[X_circles,y_circles],[X_digits,y_digits]]


figure = plt.figure(figsize=(3*len(names), 3*len(datasets)))
i = 1

for ds_cnt, ds in enumerate(datasets):
    # preprocess dataset, split into training and test part
    X, y = ds
 
 #   i += 1
    # iterate over JiangWei_models
    for name, clf in zip(names, JiangWei_models):
        ax = plt.subplot(len(datasets), len(JiangWei_models), i)
        X_transformed = clf.fit_transform(X)     
        if ds_cnt == 0:
            ax.set_title(name)


        #画出来

        digit_0 = y == 0
        digit_1 = y == 1
        digit_2 = y == 2
        digit_3 = y == 3
        digit_4 = y == 4
        digit_5 = y == 5
        digit_6 = y == 6
        digit_7 = y == 7
        digit_8 = y == 8
        digit_9 = y == 9
        ax.scatter(X_transformed[digit_0, 0], X_transformed[digit_0, 1], c="red",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_1, 0], X_transformed[digit_1, 1], c="blue",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_2, 0], X_transformed[digit_2, 1], c="green",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_3, 0], X_transformed[digit_3, 1], c="yellow",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_4, 0], X_transformed[digit_4, 1], c="cyan",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_5, 0], X_transformed[digit_5, 1], c="magenta",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_6, 0], X_transformed[digit_6, 1], c="black",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_7, 0], X_transformed[digit_7, 1], c="chartreuse",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_8, 0], X_transformed[digit_8, 1], c="darkblue",
                    s=20, edgecolor='k')
        ax.scatter(X_transformed[digit_9, 0], X_transformed[digit_9, 1], c="darkgoldenrod",
                    s=20, edgecolor='k')
        
        ax.set_xticks(())
        ax.set_yticks(())

        i += 1

plt.tight_layout()
plt.show()

2、降到三维

# 降维综合--降到三维

import numpy as np
import plotly.graph_objects as go
from plotly.subplots import make_subplots

# 导入降维算法
from sklearn.decomposition import PCA, IncrementalPCA, KernelPCA
from sklearn.manifold import MDS, Isomap, LocallyLinearEmbedding, SpectralEmbedding, TSNE
import umap

# 导入数据集
from sklearn.datasets import load_iris, make_circles, load_digits

# 定义模型名称
names = ["PCA", "IPCA", "KPCA", "MDS", "Isomap", "LLE", "SE", "T-SNE", "UMAP"]

# 修改降维模型，目标维度改为3
models = [
    PCA(n_components=3),
    IncrementalPCA(n_components=3, batch_size=10),
    KernelPCA(n_components=3, kernel="rbf", fit_inverse_transform=True, gamma=10),
    MDS(n_components=3),
    Isomap(n_components=3,n_neighbors=10),
    LocallyLinearEmbedding(n_components=3,n_neighbors=10),
    SpectralEmbedding(n_components=3,n_neighbors=10),
    TSNE(n_components=3, init='pca', perplexity=30),
    umap.UMAP(n_components=3, random_state=42)
]

# 加载数据集
iris = load_iris()
X_iris, y_iris = iris.data, iris.target

X_digits, y_digits = load_digits(return_X_y=True)

datasets = [[X_iris, y_iris],[X_digits, y_digits]]

# 定义颜色列表，用于不同类别的数据点
colors = ["red", "blue", "green", "yellow", "cyan", "magenta", "black", "chartreuse", "darkblue", "darkgoldenrod"]

# 构造子图：行数为数据集数量，列数为降维方法数量，
# 使用 type 为 "scatter3d" 来支持 3D 散点图
rows = len(datasets)
cols = len(models)
# 仅在第一行显示方法名称，其余子图标题为空
subplot_titles = []
for i in range(rows):
    for j in range(cols):
        title = names[j] if i == 0 else ""
        subplot_titles.append(title)

fig = make_subplots(
    rows=rows, cols=cols,
    specs=[[{'type': 'scatter3d'} for _ in range(cols)] for _ in range(rows)],
    subplot_titles=subplot_titles,
    horizontal_spacing=0.02,
    vertical_spacing=0.05
)

# 遍历每个数据集和每个降维模型
for ds_idx, (X, y) in enumerate(datasets):
    for model_idx, (name, model) in enumerate(zip(names, models)):
        # 对数据进行降维处理，得到三维表示
        X_transformed = model.fit_transform(X)
        
        # 针对数据中的每个类别添加一个散点图
        unique_labels = np.unique(y)
        for label in unique_labels:
            mask = y == label
            trace = go.Scatter3d(
                x = X_transformed[mask, 0],
                y = X_transformed[mask, 1],
                z = X_transformed[mask, 2],
                mode = 'markers',
                marker = dict(
                    size = 3,
                    color = colors[int(label)]
                ),
                name = str(label),
                showlegend = False  # 每个子图不单独显示图例
            )
            fig.add_trace(trace, row=ds_idx+1, col=model_idx+1)

# 隐藏每个子图的坐标轴刻度
total_subplots = rows * cols
for idx in range(1, total_subplots+1):
    scene_id = 'scene' if idx == 1 else f'scene{idx}'
    if scene_id in fig.layout:
        fig.layout[scene_id].xaxis.update(showticklabels=False)
        fig.layout[scene_id].yaxis.update(showticklabels=False)
        fig.layout[scene_id].zaxis.update(showticklabels=False)

# 调整整个图的布局
fig.update_layout(
    height=300 * rows,
    width=300 * cols,
    title_text="3D降维方法对比"
)

fig.show()

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值