不相交集合的数据结构（Disjoint Sets）

啵啵张

已于 2024-02-07 17:57:10 修改

阅读量222

点赞数

文章标签：数据结构算法图论

于 2023-08-30 19:42:32 首次发布

本文链接：https://blog.youkuaiyun.com/m0_56945100/article/details/132528362

版权

一、不相交集合的操作

1、基本操作

$MAKE-SET\left ( x \right )$ ：建立一个新的集合，它的唯一成员是 $x$ 。

$UNION\left ( x,y \right )$ ：将包含x和y的两个动态集合（ $S_{x}$ 和 $S_{y}$ ）合并成一个新的集合。

$FIND-SET\left ( x \right )$ ：返回一个指针，这个指针指向包含 $x$ 的唯一的集合代表。

我们使用如下两个参数衡量时间复杂度：

$n$ ：MAKE-SET操作次数。

$m$ ：MAKE-SET、UNION、FIND-SET操作总次数。

2、Disjoint Sets的一个应用：无向图的连通分量

不相交集合数据结构的应用之一是确定无向图的连通分量。CONNECTED-COMPONENTS使用不相交集合数据结构来计算无向图的连通分量，SAME-COMPONENT回答两个顶点是否在同一个连通分量。

举例：

二、不相交集合的链表表示

1、用链表实现的Disjoint Sets

每个集合用一个自己的链表来表示。每个集合对象包含head和tail属性，head指向表的第一个对象，tail指向表的最后一个对象。链表中的每个对象都包含一个集合成员、一个指向链表中下一个对象的指针和一个指回到集合对象的指针。

例如：

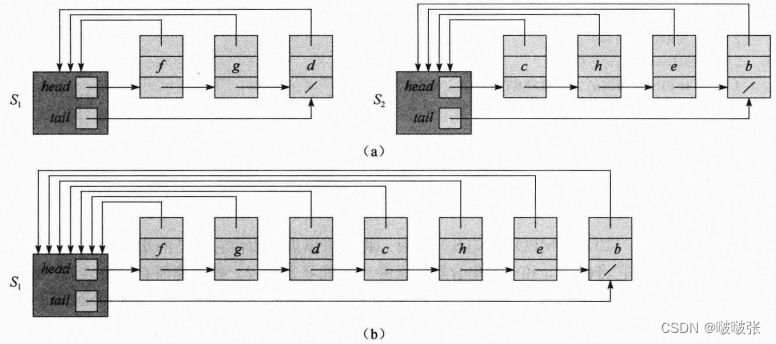
时间复杂度：平均情况下，MAKE-SET： $O\left ( 1 \right )$ ；FIND-SET： $O\left ( 1 \right )$ ；UNION： $O\left ( n\right )$ 。

特点：FIND-SET快，UNION慢。

2、一种加权合并的启发式策略

加权合并启发式策略：总是将较短的表拼接到较长的表中。

定理：使用不相交集合的链表表示和加权合并启发式策略，一个具有 $m$ 个MAKE-SET、UNION、FIND-SET操作的序列（其中 $n$ 个是MAKE-SET操作）需要的时间为 $O\left ( m+nlgn \right )$ 。

时间复杂度：平均情况下，MAKE-SET： $O\left ( 1 \right )$ ；FIND-SET： $O\left ( 1 \right )$ ；UNION： $O\left ( lgn \right )$ 。

三、不相交集合森林

1、用森林实现的Disjoint Sets

在一个不相交集合森林中，每个成员仅指向它的父结点，根结点是代表，且是自己的父结点。

特点：FIND-SET慢，UNION快。

2、改进运行时间的启发式策略

通过使用如下两种启发式策略，我们能获得一个几乎与总的操作数 $m$ 呈线性关系的运行时间。

策略一按秩合并（union by rank）：让具有较小秩的根指向具有较大秩的根。对于每个结点维护一个秩，它表示该结点高度的一个上界。

时间复杂度：当仅使用按秩合并策略时，平均情况下，MAKE-SET： $O\left ( 1 \right )$ ；FIND-SET： $O\left ( lgn \right )$ ；UNION： $O\left ( lgn \right )$ 。

策略二路径压缩（path compression）：在FIND-SET操作中，该策略可以使查找路径中的每个结点直接指向根。路径压缩并不改变任何结点的秩（因为如果每次路径压缩都更新结点的秩这将非常耗时，且没有必要）。

路径压缩：

伪代码（ $x.rank$ 代表高度的一个上界，每个FIND-SET操作不改变任何秩。UNION操作有两种情况：如果根没有相同的秩，则让较大秩的根成为较小秩的根的父结点，但秩本身保持不变；如果两个根有相同的秩，任选其中一个根为另一个根的父结点，并使其秩加1.）：

解释：FIND-SET过程是一种两趟方法：当它递归时，第一趟沿着查找路径向上直到找到根，当递归回溯时，第二趟沿着搜索树向下更新查找路径上每个结点，使其直接指向根。

时间复杂度：当同时使用按秩合并和路径压缩时，平均情况下，MAKE-SET： $O\left ( 1 \right )$ ；FIND-SET： $O\left ( lg^{*}n \right )$ ；UNION： $O\left ( lg^{*}n \right )$ （函数 $lg^{*}x$ 取值如下表）。最坏情况的总运行时间为 $O\left ( mlg^{*}n \right )$ ，其中 $lg^{*}n$ 是增长非常缓慢的函数，在实际应用中我们可以认为 $lg^{*}n\leq 4$ 。因此可以认为运行时间是 $m$ 的线性函数。