本文档详细介绍了三个Java编程问题的解决过程，涉及幻方的合法性判断与生成、TurtleGraphics图形绘制（正多边形、凸包计算）以及社交网络无向图的实现。实验涵盖了文件读取、异常处理、图形算法、面向对象设计以及图论基础知识，旨在提升Java编程和问题解决能力。
目录
4.1 Problem 1: Clone and import
4.2 Problem 3: Turtle graphics and drawSquare
4.3 Problem 5: Drawing polygons
4.4 Problem 6: Calculating Bearings
4.5 Problem 7: Convex Hulls
4.6 Problem 8: Personal art
1.实验目标概述
本次实验通过求解三个问题，训练基本Java编程技能，能够利用Java OO开发基本的功能模块，能够阅读理解已有代码框架并根据功能需求补全代码，能够为所开发的代码编写基本的测试程序并完成测试，初步保证所开发代码的正确性。另一方面，利用Git作为代码配置管理的工具，学会Git的基本使用方法。
- 基本的Java OO编程
- 基于Eclipse IDE进行Java编程
- 基于JUnit的测试
- 基于Git的代码配置管理
2.实验环境配置
- 在本机安装jdk8并配置环境变量，在系统变量中增加名为%JAVA_HOME%的变量，在PATH增加bin路径。修改完成后在命令行中测试，显示如下，安装成功。
2.在本机安装Eclipse，更换安装目录。
3.在本机安装Git，综合网上多份教程完成了安装配置地数十个步骤。
4.下载Junit并在Eclipse IDE中配置。在官网下载它的jar包，在要使用Junit的project名上，点击properties—java build path---libraries，点击Add External JARs，将包加入。
3.问题一 Magic Squares
该任务主要实现的是对n阶幻方的判定。
第一个任务要求从5个文件读入并分别判断，这部分的操作难点是文件读入和对于各种各样异常情况（行列数不相等、并非矩阵、矩阵中的某些数字并非正整数、数字之间并非使用\t分割等）的合理处理与提示，需要对java的相关操作和判断的层次结构有一定的掌握。如果文件中的内容是合法的且被顺利地读入到了int数组中，接下来就很容易对其进行判断。
第二个任务是给定了生成幻方矩阵的函数，对该函数的流程与其异常情况进行分析，之后扩展函数并调用上一问写好的函数对其幻方性进行判定。
3.1 isLegalMagicSquare（）
3.1.1 文件路径设置
为了增加程序的可移植性，采用相对路径，先使用System.getProperty("user.dir")得到程序当前所在路径，再根据题目要求的相对路径建立各个txt文件的绝对路径，在主函数中分别判断5个txt文件。
3.1.2 文件内容的读入
导入java.io中相应的包，因为不知道矩阵大小，用ArrayList<String>存储读出的内容，用BufferedReader每次读取一行，将这一行加在ArrayList<String>的后面，直到读入为空。
3.1.3 转换为整型数组
用ArrayList<String>的length可以得到矩阵的行数，每行使用split函数去掉”\t”后可以得到该行的列数，只有行列相等时才会继续进行判断。否则要么是第一行使用了”\t”以外的分隔符，要么是矩阵行列数不相等。
新建一个int型的数组，用两层循环转换每一个数，在每一行的开始都要判断该行有多少个数字。与原先列数不相等时，考虑到可能存在的其他分隔符，split同时去掉可能有的所有空格和逗号，再比较长度，如果相等输出间隔符错误信息；否则输出非矩阵的错误信息。
在正常情况下时，用String接受ArrayList<String>中的该行元素，当其不符合正整数的正则表达式时，提示数据不合法并返回false，否则将其用Integer.valueOf转换为整型数并存储在数组中。
3.1.4 检查幻方性
上述所有工作都正常完成后，在整型数组中检测其是否符合幻方矩阵。分别检测其行、列和对角线的和。
3.1.5 输出结果
3.2 generateMagicSquare（）
3.2.1 函数程序流程解释
程序初始化第一个固定的位置后，根据i与n的关系和上一步初始化的元素位置来确定下一个初始化的元素的位置，依次为1、2、3，…。
先在矩阵第一行中间的位置上放1，然后把数字按照升序沿着右上角放置到矩阵中。如果越界了，就假设周围还有一个矩阵，将数字放到那个位置上；如果那个位置已经被占据了，就跳过该位置放到下面的位置，然后重新按照原来的方法放。如图：在5×5的魔术矩阵中，放完1以后，就把2放到1的右上角，但是此时已经越界了。假设，在原来的矩阵上面还有一个矩阵，则数字2所放的位置应该是在最后一行的第二个位置，接下去就要把数字3放到2的右上角，依次放下去，当放到6的时候，由于1已经将下一个位置占了，所以就放到5下面的位置。依照这样的规律直到把数字都放完。
因为相邻数字相差为1，将其放在右上角可以保证涉及到的两行和两列各自的差是1，对row是否等于0和对col是否等于n-1的判断就是为完成矩阵内的回环。
因为有对i%n是否为0的判断。当不等于0时，把相邻的5个数分别放在不同的行和列上；当等于0时，放置这五个数中的第一个的起始行会发生变化，列不变，这种做法循环不断弥合着列上和与行上和的差距，最终达到相等。
在次对角线上输入的势必为1到n^2中间的n个数，是该幻方矩阵的和。
3.2.2 函数异常行为解释
在输入奇数时，对于次对角线的填充是从最下面开始的，结束时可以顺利开始接下来n个数的填充。可是输入为偶数时，是从倒数第二行开始填充的，结束时在最后一行，当开启接下来n个数的填充时，数组就越界访问到了最后一行的下一行，造成了ArrayIndexOutOfBoundsException的越界错误。
在输入负数时，程序无法正常的申请数组并对数组元素赋值，造成了NegativeArraySizeException的错误，arraysize要为正数。
4.问题二 Turtle Graphics
该任务主要是：clone已有的程序后，利用turtle按照要求画图并实现一系列的在TurtleSoup中的方法，方法都有给定的规约，由浅入深，逐步实现。
先是画出一个正方形的drawSquare，到用边数计算正多边形内角和用正多边形内角计算边数的基本边角转换，之后实现画出不同边数正多边形的drawRegularPolygon；计算从一个点到另外一个点所需要转过的角度，给定一系列点计算每次转过的角度并返回在List中；计算一系列点中的凸包；调用函数绘制个人艺术作品。以上除绘图的方法都使用junit进行测试。
4.1 Problem 1: Clone and import
从GitHub的某个网站上下载获取该任务的代码，在本地创建git仓库，使用git管理本地开发。
用git config设置自己账号的名字和邮箱。用cd ~/.ssh生成密钥，在系统根目录下找到.ssh文件夹，找到id_rsa.pub文件，复制密钥到Github账户进行配置。找到settings中的 SSH and GPG keys ，点击 NEW SSH key，写上定义的名字，并粘贴SSH 密钥。
在要上传的目录中打开 Git Bash， 用git init初始化本地仓库，用git add . 和git commit -m “注释”将本地文件放入本地仓库。
用“git remote add origin 仓库地址”建立好本地仓库与远程仓库的关联，用“git push -u origin master”将本地库的内容推到远程仓库。
4.2 Problem 3: Turtle graphics and drawSquare
通过四次循环，每次前进与90°转向即可绘制出正方形。结果如下。
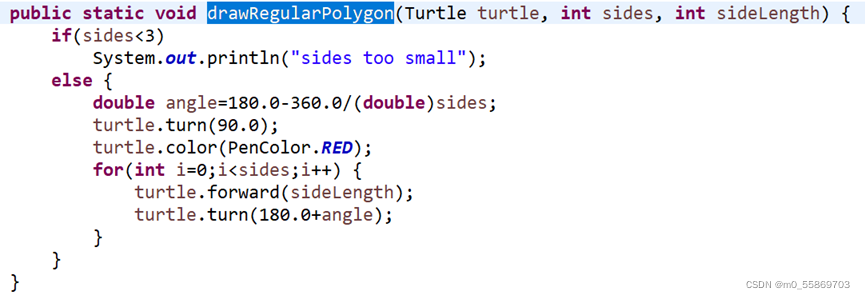
4.3 Problem 5: Drawing polygons
补全calculateRegularPolygonAngle，利用输入的正多边形的边数计算其内角，正多边形内角和为180*(n-2)，每个内角相等，除以n得到180-360/n，n为int而返回值为double，公式中进行类型强转。
补全calculatePolygonSidesFromAngle，利用输入的正多边形的内角度数计算其边数，将上一个公式的所求进行转换即可得到。考虑到是从double转向int，直接转换会导致部分值无法顺利进位，因此使用Math.round先进行四舍五入再转换类型。
完成绘制正多边形的方法drawRegularPolygon，通过其输入sides决定绘制几边形。对输入判断，sides<3时错误，不绘图；此外，调用calculateRegularPolygonAngle计算多边形内角，每次转向都是180°+内角。
从0开始到9，依次调用该函数，将其绘在一张图上，可以看到函数书写正确。
4.4 Problem 6: Calculating Bearings
实现calculateBearingToPoint，已知起点和当前朝向角度，要求起点到终点需要转动的角度。对可能存在的情况进行考虑，使用arctan函数，在不同情况下返回不同值作为转向角度。程序代码如下：
首先使用Math.atan2方法计算两点之间的边与x轴正半轴所成的弧度并转换成角度值angle；因为turtle旋转的方向是顺时针，极坐标角度的旋转方向是逆时针，所以angle取负；因为turtle的 0° 线向上，坐标轴的 0° 线向右，从顺时针角度看中间少了 90°，因此再加上90°；然后减去turtle当前朝向角度currentBearing；最后将角度调整到 0 - 360° 之间（正角度）。
实现calculateBearings，这是上述问题的扩展，此时有n个点，要求从第一个点开始到第二个点，再从第二个点到第三个点，得到n-1个转向的角度，存在List中。以起点为第一个点，循环n-1次，每次将第i号点设置为起点，将第i+1号点设置为终点，通过上一个函数计算旋转角度并存储到List中。程序代码如下：
4.5 Problem 7: Convex Hulls
实现了convexHull，点数小于等于3个则直接将这些点输出为凸包，否则使用gift wrapping算法对凸包进行求解。
先找到所有点中最左下方的点，这是找到的第一个凸包中的点，将其作为起始点，找剩余点中从0°方向逆时针转向最小的点。也就是调用上面的calculateBearingToPoint，在初始为90°时得到转过的角度，找到角度最大的；如果有多个，要求边最短的，依次加入，再用上一个加入的求出下一个。
这其中使用了temp这个新集合，复制了原来输入的点集，每次得到一个凸包中的点就把它从temp中删除，保证不会重复。从左下点开始，最终一定会回到左下点，此时结束循环，得到正确的凸包。
4.6 Problem 8: Personal art
完成drawPersonArt函数，用到之前完成的绘制正多边形的函数，先用红色画笔从原点开始绘制边数从3到14的正多边形，之后用蓝色画笔绘制正五边形和嵌套在其中的五角星。
4.7 Submitting
编写完成，绘图正常，Junit测试全部通过。
打开git bash，使用git add . 和git commit “v2.1_1and2finished”，之后git push origin master 推送到远程仓库，完成提交。
5.问题三 Social Network
该任务主要是设计一张社交网络无向图，表示人与人之间的关系，并且可以计算图中两个人之间的距离，要求该无向图可以扩展到有向图。
图被定义在FriendshipGraph类中，用一个集合记录图中已有的点，应该实现的操作有加点、加边、getDistance得到两个人之间的最小距离。还应该为图中的每个节点——即每个人建立一个Person类，在类中定义person的名字、朋友集，分别编写get和set来得到或修改它们。
在getDistance方法中，要求的是无向无权图的最短距离，可以使用广度优先算法。
5.1 设计/实现FriendshipGraph类
使用一个set来存储已经加入到图中的点(Person)。
在addVertex方法中，先在上面的集合中判断有无同名的人已经被加入到图中，若有，则终结程序且输出错误提示；否则将这个Person加入到set中。
在addEdge方法中，考虑到要支持未来扩展到有向图，因此加边的操作是把第二个Person加入到第一个Person的朋友集中。在当前的无向图中，要求加一条边调用该方法两次。
在FriendshipGraph中，并不需要调用Java存在的图类或者使用邻接矩阵等来存储边，只需要将边也就是对应的朋友关系存在这个人的个人属性中，即存在Person中。定义若p2是p1的朋友，则p2在p1的朋友集中，代表图中有p1到p2的一条边。
在getDistance方法中，求p到q的距离（在无向图中两者顺序对结果不产生影响，但考虑到向有向图的扩展，需要有所区别）。使用temp这个set来存储所有未被访问过的节点（初始是除p以外的所有结点），在Person中添加一个qua，用来存储节点是第几个被访问到的。主体部分是广度优先搜索算法，为了区分不可达的情况，一个可达的队列变空而还有点未被访问到时，就令qua加一个极大的数值（设为100000）。如果p与q的qua数值相差超过90000，就认为不连通返回值为-1，否则返回两者的差。这样设计充分考虑到了图较大的情况。
5.2 设计/实现Person类
Person类包括名字、朋友集、qua（在getDistance方法中用到），包括的方法有初始化、getName、getFriend、getQua、setQua与addFriend等基本方法。
5.3 设计/实现客户端代码main()
测试代码及结果如下。
5.4 设计/实现测试用例
在addVertexTest中，每加入一个点，测试该点和之前加入的点已经包含在了图中，其余点未包含。
在addEdgeTest中，加入边并测试对应Person的朋友集中是否成功加入。在该测试中，看到了未来对于有向图的可扩展。
在getDistance中，由题中规定，加一条边调用两次语句是由客户端完成的，因此我们测试有向图与无向图的getDistance，本质上是相同的。因此输入一个较复杂的有向图，如下。
部分测试代码如下：
测试结果全部正确。
6.实验收获与感想
在实验中使用了git、eclipse等从未使用过的软件和从未接触过的面向对象的编程语言Java，在实验初期的环境安装和代码编写中遇到了较大的困难，但随着完成实验内容，逐渐掌握了Java的编写方法，对于git和junit的使用也有了一定的经验。
以上三个问题除了一些最基本的编程要求外，问题1帮助我们熟悉了文件的读入和输出、split的使用、从文件转换到数组等操作；问题2帮助我们熟悉了turtle类、junit的用法以及凸包算法；问题3帮助我们了解了Java中的Map、Set、List等内容以及test的编写还有面向对象的编程方法。这三个实验结合起来，有助于初学者迅速上手Java。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
