DYffusion阅读笔记 “DYffusion: A Dynamics-informed Diffusion Model for Spatiotemporal Forecasting“

最新推荐文章于 2025-04-17 11:41:29 发布

原创最新推荐文章于 2025-04-17 11:41:29 发布 · 2k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#笔记

部署运行你感兴趣的模型镜像

引言

动态预测是指预测动态系统未来行为的任务，设计学习控制系统演化的潜在动态，以对其未来状态做出准确的预测。高斯diffusion在正向过程中使用高斯噪声不同程度地破坏数据，然后通过反向过程对随机输入进行去噪以得到高度真实的样本。然而，在高维度上将噪声映射到真实数据十分具有挑战性，因此扩散模型的计算成本非常高。而且，扩散模型多用于静态图像，即使是能生成真实样本的video diffusion model也没有明确利用数据的时间性质来生成准确的预测。

本文贡献：

从扩散模型的角度研究概率时空预测。
提出了用于多步骤预测和长期视野的DYffusion框架，此框架通过时间归纳偏差来加速训练和降低内存要求。并且探讨了该方法的理论含义，DYffusion是学习动力系统解的隐式模型，cold sampling可以解释为它的欧拉方法解。
从预测性能和算力要求两个方面与conditional video diffusion models等先进的概率方法进行对比试验。结果表明，相较于高斯扩散模型，DYffusion提高了计算效率。

背景

问题提出

给定一组快照数据集 $\left \{ \rm{x}_t \right \} _{t=1}^T \in \mathcal{X}$ （ $\mathcal{X}$ 由空间维度（例如纬度、经度和大气高度）和通道维度（例如速度、温度和湿度）组成，表示数据所在的空间），概率预测的任务是学习条件分布 $P(\rm{x}_{t+1:t+h}|\rm{x}_{t-l+1:t})$ ，用l张过去的快照来预测接下来连续的h个快照。本文从单个初始条件开始进行预测任务，即学习 $P(\rm{x}_{t+1:t+h}|\rm{x}_{t})$ 。

扩散过程

为了将扩散步骤的状态和 $\left \{ \rm{x}_t \right \} _{t=1}^T$ 的时间步区分开，我们用上标n来表示扩散步状态 $s^{(n)}$ 。这个操作可以概括为，假设我们有一个退化算子D，以数据点 $s^{(0)}$ 为输入，针对不同程度的退化比例输出 $s^{(n)}=D(s^{(0)},n)$ ， $n \in \left \{1,...,N \right \}$ 。通常，D加入带有递增方差的高斯噪声使得 $s^{(N)}\sim \mathcal{N} (\mathbf{0},\mathbf{I})$ 。使用 $\theta$ 参数化一个去噪网络，训练 $R_{\theta }$ 来恢复 $s^{(0)}$ 。扩散模型可以通过考虑 $R_{\theta }(s^{(n)},\rm{x}_t,n)$ 来根据输入动态进行条件设定。在动态预测中，可以训练扩散模型以最小化目标：

$\underset{\theta }{min} \ \mathbb{E}_{n \sim \mathcal{U} [\![1,N]\!],\rm{x}_t,s^{(0)} \sim \mathcal{X} }[\left \| R_{\theta }(D(s^{(0)},n),\rm{x}_t,n)-s^{(0)} \right \|^2]$

其中， $\mathcal{X}$ 是数据分布， $\left \| \cdot \right \|$ 是范式， $s^{(0)}=\rm{x}_{t+1:t+h}$ 是预测目标。 $\mathcal{U} [\![a,b]\!]$ 是集合 $\left \{ a,a+1,...,b\right \}$ 上的均匀分布，在实践中，可以训练 $R_{\theta }$ 来使用score matching objective来预测加到数据中的高斯噪声。

DYffusion: DYnamics-Informed Diffusion Model(动力学信息扩散模型)

本文使用随机插值器网络 $\mathcal{I} _{\phi }$ 替换退化算子D，使用确定的预测器网络 $F_{\theta }$ 替换恢复网络 $R_{\theta }$ 。从高层次上讲，我们的正向过程和反向过程模拟了数据中的时间动态。因此，扩散过程中的中间步可以用来在多步预测中进行预测。另外，与标准扩散模型中逆过程从白噪声不同，本文的逆过程从观测到的数据开始，所需的步骤更少，而且整个过程都受观测到的数据约束，可以提高预测的准确率。

时间插值作为前向过程

为了设置时间偏差，我们训练了一个时间条件网络 $\mathcal{I} _{\phi }$ 在数据快照之间进行插值。具体来说就是，在范围h上，使用下述目标来训练 $\mathcal{I} _{\phi }$ ，使得 $\mathcal{I} _{\phi }(\mathbf{x}_t,\mathbf{x}_{t+h},i)\approx \mathbf{x}_{t+i},\ i \in \left \{ 1,...,h-1 \right \}$ （让 $\mathcal{I} _{\phi }$ 学习到数据的动态变化规律）：

$\underset{\phi }{min}\ \mathbb{E}_{i \sim \mathcal{U}[\![1,h-1]\!] ,\mathbf{x}_{t,t+i,t+h} \sim \mathcal{X}}[\left \| \mathcal{I}_{\phi }(\mathbf{x}_t,\mathbf{x}_{t+h},i)-\mathbf{x}_{t+i} \right \|^2]$

使用 $\mathcal{I} _{\phi }$ 可以得到比原始数据具有更高时间分辨率的数据。也就是说，时间输入可以是连续的，其中 $i \in (0,h-1)$ ，且(0,1)不在训练范围内。为了生成概率预测，插值器 $\mathcal{I} _{\phi }$ 在扩散模型和推理时间内产生随机输出至关重要。我们在推理时使用蒙特卡罗 dropout 来实现这一点。

蒙特卡洛dropout(Monte Carlo Dropout)

蒙特卡罗dropout在训练阶段以传统dropout的方式工作，即随机丢弃部分神经元的输出，以减少神经元之间的共适应，从而防止过拟合。然而，在测试（或推理）阶段，蒙特卡罗dropout的用途发生了转变。它保持dropout层处于激活状态，并对同一个输入进行多次前向传播，每次前向传播都可能丢弃不同的神经元，从而产生多个不同的预测结果。这些预测结果的分布可以用来估计模型的不确定性。

预测作为逆过程

在第二步中，我们训练一个预测网络 $F_{\theta }$ 来预测 $\mathbf{x}_{t+h}$ 使得 $F_{\theta }(\mathcal{I}_{\phi }(\mathbf{x}_t,\mathbf{x}_{t+h},i|\xi ),i)\approx \mathbf{x}_{t+h}$ ，其中 $\ i \in S=[i_n]_{n=0}^{N-1}$ ，S表示扩散步骤映射到时间插值步骤的时间表。在随机性推理过程中，插值网络 $\mathcal{I} _{\phi }$ 保持不变， $\xi$ 表示随机丢弃的权重。目标函数如下：

$\underset{\theta }{min}\ \mathbb{E}_{n \sim \mathcal{U} [ \![0,N-1] \!], \mathbf{x}_{t,t+h} \sim \mathcal{X}}[\left \| F_{\theta }(\mathcal{I_{\phi }}(\mathbf{x}_{t}, \mathbf{x}_{t+h},i_n|\xi ),i_n)-\mathbf{x}_{t+h} \right \|^2]$

为了使 $F_{\theta }$ 学习到初始条件，我们定义 $i_0:= 0,\ \mathcal{I}_{\phi }(\mathbf{x}_t,\cdot ,i_0):= \mathbf{x}_t$ 。在最简单的情况下，预测网络被所有可能的时间步长监督，这些时间步长由训练数据的时间分辨率给出。也就是， $N=h$ ， $S=[j]_{j=0}^{h-1}$ 。一般情况下，插值时间步应该满足：当 $0<n<m\leq N-1$ 时， $0=i_0< i_n< i_m< h$ 。鉴于我们的预测器和去噪网络在扩散模型中的等效作用，我们也将它们称为扩散主干。这意味着预测网络不仅可以用于预测未来或缺失的数据，还可以像扩散模型中的去噪网络一样，逐步去除噪声以恢复数据。值得注意的是，扩散骨干的时间条件是基于 $i_n$ 而不是n，因此在训练或推理过程中可以选择任何diffusion-dynamics schedule。这意味着预测网络可以灵活地适应不同的时间尺度或数据特性，甚至可以对未见过的时间步进行预测。

由于在第二阶段中 $\mathcal{I} _{\phi }$ 保持不变，因此在顺序采样中 $\hat{\mathbf{x}}_{t+h}=F_{\theta }(\mathcal{I}_{\phi }(\mathbf{x}_t,\mathbf{x}_{t+h},i_n),i_n)$ 的准确率可能会降低。为了解决这个问题，当n+1<N时，我们引入了一部步look-head损失项 $\left \| F_{\theta }(\mathcal{I}_{\phi }(\mathbf{x}_t,\hat{\mathbf{x}}_{t+h},i_{n+1}),i_{n+1})-\mathbf{x}_{t+h} \right \|^2$ ，并使两个损失项的权重相等。除此之外，提供初始为干净或噪声形式的 $\mathbf{x}_t$ 作为预测网络的额外输入有助于改善性能。

下面时这两个阶段的训练算法：

采样

综上所述，我们可以将DYffusion的生成过程写为：

$p_{\theta }(s^{(n+1)}|s^{(n)},\mathbf{x}_t)=\left\{\begin{matrix} F_{\theta }(s^{(n)},i_n)&if \ n=N-1 \\ \mathcal{I}(\mathbf{x}_t,F_{\theta }(s^{(n)},i_n),i_{n+1})&otherwise \end{matrix}\right.$

其中 $s^{(0)}=\mathbf{x}_t, s^{(n)} \approx \mathbf{x}_{t+i_n}$ 分别对应于初始条件和中间步骤的预测。在公式中，我们反转了扩散步骤的索引以与数据的时间索引保持一致，即当n=0时反向过程开始（ $\mathbf{x}_t$ ），当n=N指的是反向过程的最终输出（ $\mathbf{x}_{t+h}$ ）。与标准扩散模型中从噪声到数据的映射相反，我们的反向过程在时间上向前推进。因此，DYffusion所需的扩散步骤和数据较少。

我们的插值阶段阶段不是扩散过程，但是预测阶段却遵循广义扩散模型的目标。这允许我们使用现有的扩散模型的采样方法进行推理，例如冷采样(Algorithm 2)。 $F_{\theta }$ 对最后一个时间步 $\mathbf{x}_{t+h}$ 进行预测，但是随着时间上接近t+h，它会迭代地改进这些预测。这类似于标准扩散模型中“干净”数据的迭代去噪。这体现在Algorithm 2的第六行中， $\mathbf{x}_{t+h}$ 的最终预测值可用于微调中间预测或者增加预测的时间分辨率。如下图所示，在我们的方法中，插值和预测是交替进行的。

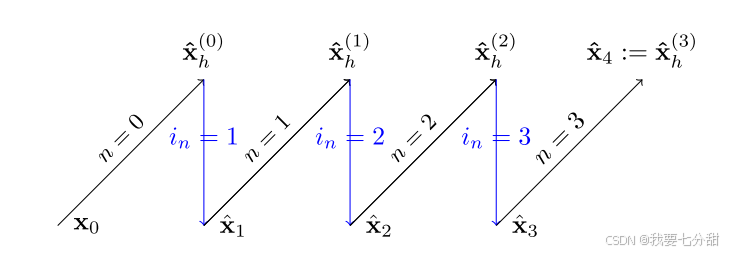
内存占用率

DYffusion只需要训练 $\mathbf{x}_{t}$ 和 $\mathbf{x}_{t+h}$ ，第一阶段还要训练 $\mathbf{x}_{t+i}$ ，所以无论h如何变化，内存占用都保持恒定。相反，包括视频扩散模型在内的直接多步预测模型需要 $\mathbf{x}_{t:t+h}$ 来计算损失。这意味着这些模型必须将h + 1个时间步长的数据放入内存中。因此，许多算法仅限于预测少量的帧。例如，由于GPU内存限制，MCVD最多只能训练5个视频帧。

反向过程的ODE

DYffusion可以理解为通过“扩散过程”来模拟动态，类似于隐式模型。这种角度有助于解释DYffusion优越的预测能力，因为它学习模拟物理动力系统 $\mathbf{x}_{t}$ 。训练 $F_{\theta }$ 和 $\mathcal{I} _{\phi }$ 来构造一个微分方程，隐式地模拟 $\mathbf{x}_{t}$ 的解。

令s为时间变量，DYffusion的动态变化可定义为：

$\frac{d\mathbf{x}(s)}{ds}=\frac{\mathcal{I}_{\phi }(\mathbf{x}_t,F_{\theta }(\mathbf{x},s),s)}{ds}$

给定初始状态为 $\mathbf{x}(t)=\mathbf{x}_{t}$ ，在训练过程中，我们尝试求：

$\mathbf{x}(s)=\mathbf{x}(t)+\int_{t}^{s}\frac{d\mathcal{I}_{\phi }(\mathbf{x}_t,F_{\theta }(\mathbf{x},s),s)}{ds}ds \ for \ s \in(t,t+h]$

当进行离散预测时，预测过程就等价于上式。采样表 $i_n$ 可以看作ODE求解器中的步长。因此可以在推理过程中灵活地选择采样表，因为他们是相同的ODE离散化。冷采样是与欧拉方法最接近的采样算法。

把DYffusion看作一个隐式模型强调了其动态本质且解释了DYffusion和DDIM的关系。DDIM可以看作一个从随机图像到干净图像的动态噪声去除模型。DYffusion可以看作一个从动态系统的当前步 $\mathbf{x}_t$ 到未来步 $\mathbf{x}_{t+h}$ 的隐式求解模型。

您可能感兴趣的与本文相关的镜像

Stable-Diffusion-3.5

图片生成

Stable-Diffusion

Stable Diffusion 3.5 (SD 3.5) 是由 Stability AI 推出的新一代文本到图像生成模型，相比 3.0 版本，它提升了图像质量、运行速度和硬件效率