一趟排序放在最终位置
/*
一趟排序结束后不一定能够选出一个元素放在其最终位置上的是()。
正确答案: D
堆排序
冒泡排序
快速排序
希尔排序
最终位置不是最大或者最小值
可以是中间位置
A、堆排序可以把最大的或者最小的放在堆顶,所以是可以在一趟排序之后将其中一个放在最终位置的
堆排序一趟下来就可以将最大或最小值放在堆顶
然后是堆顶下面的做调整
B、冒泡排序在一趟排序之后把最大的放在了最右边
C、快速排序的过程是选出一个作为基准,大的放在基准的右边,小的放在基准的左边
然后递归实现,所以基准是可以放在最终的位置的
D、希尔排序属于插入排序,而插入排序是不能保证在第一次排序后放在最终位置
故选D
堆排序,每次循环将堆顶这个最大数放到数组右边,就是其最终位置
冒泡排序,每次循环,将未排序中最大的数放到数组右边其最终位置
快速排序,每次分割,都要将分割的基准放到中间,就是其最终位置
希尔排序,是先大跨度的插入排序,再小跨度调整,每次插入都会移动以前插入的数据
堆排序的思路重新构建一下
首先将待排序的数组构建成一个大顶堆
将其与末尾元素交换
此时末尾元素就是最大值
然后将其余n-1个元素重新构建成一个堆
此时就能得到n个元素的次大值了
如此反复执行
就能得到一个有序序列了
*/
二路归并的排序过程
/*
对于初始关键字(67,66,77,82,78,51,58),使用二路归并排序,第一趟归并之后其序列变为
正确答案: B
66,67,77,82,51,58,78
66,67,77,82,51,78,58
51,58,66,67,77,78,82
67,66,77,78,82,51,58
按照顺序两两组合,每个组里两个元素进行排序
最后一个元素落单不去管
归并排序抽象排序思路是
先把数组拆分成两两组合的最小单元
然后再两两归并成4个
这样成2的幂次方增长
如果是奇数的话,最后一个落单元素
可能会在最后和排好序的整体数组进行归并
找到合适的位置并插入
*/
归并排序相较于快速排序的优点
/*
合并排序相对于快速排序的优点不包括()
正确答案: C
是稳定的
最坏的情况更高效
空间复杂度低
不会退化
当数据量越来越大时
归并排序:比较次数少,速度慢
快速排序:比较次数多,速度快
快速排序的优势越来越明显
归并排序所需要的额外空间为n
退化的意思是
举个例子,如果数组大致有序,对它进行快排,就退化成了冒泡排序
就是其最坏情况下与冒泡排序就一样了,此时我们称他退化
归并排序最好和最坏的情况一样
排序方式
in-place
比如借助辅助变量
冒泡排序中交换位置
使用了tmp变量
out-place
开辟的辅助空间与问题规模有关
比如归并排序需要创建临时数组
来放入归并的结果
排序的稳定性
我的理解是对于两个相同的元素,是否会交换相对位置
如果交换了,就是破坏了数字序列的原有稳定性
选择排序是给每个位置选择当前元素最小的,
举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,
那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法
排序算法口诀
选快希堆不稳(选择、快速、希尔、堆都是不稳定的排序)
堆归选基不变(堆、归并、选择、基数的时间复杂度不发生变化)
*/
hash表排序
/*
对n个数字进行排序,期中两两不同的数字的个数为k,
n远远大于k,
而n的取值区间长度超过了内存的大小,时间复杂度最小可以是
正确答案: A
O(nlogk)
O(nk)
O(n)
O(nlogn)
我的理解是这样的,先是用比较的方式将n个数字
通过hash函数来压缩数据的长度(键值对的形式)
花费O(n)
压缩过后,不同的数的个数就是K级别的了
然后进行排序即O(klogk)或者已经有序O(1)
那么总的复杂度近似为O(n)
两两不同的数字的个数为k,因为不知道确定的数字范围,桶排序不适合
又因为n远远大于k,本题使用hash表来统计
相同的值记录在一个链表中
首先获得k个数及其每个数出现的次数,然后对k个数进行排序
排序的复杂度可忽律不计,实际上就是遍历一遍n个数字,所以本位复杂度为O(n)
*/
拓扑排序序列
/*
已给下图,哪一项是该图的拓扑排序序列( )
1->2 1->3
2->3 2->4
3->4
4->5
1,2,3,4,5
1,3,2,4,5
1,2,4,3,5
1,2,3,5,4
求拓扑结构序列
首先找到没有任何指针指向发节点
找到1
此时将1抽出
删除1对外指向的指针
也就是
1->2 1->3
两条指针删除
此时2没有任何指针指向
将2抽出
就是这种思路
最终得到抽出的序列就是
拓扑结构
本题得到1,2,3,4,5
*/
快速排序算法适用场景
/*
以下哪种排序算法对[1, 3, 2, 4, 5, 6, 7, 8, 9]进行排序最快
正确答案: A
改良的冒泡排序
快速排序
归并排序
堆排序
改良的冒泡排序,当一轮循环中没有交换就结束排序
所以只要2轮循环
该数组只有一个位置是无序的
快速排序会把这个
已基本有序却反而变得更复杂
排对越混乱的数据
排序效果越好
*/
第1趟快速排序
/*
设一组初始关键字记录关键字为(19,15,12,18,21,36,45,10)
则以19位基准记录的一趟快速排序结束后的结果为()
正确答案: A
10,15,12,18,19,36,45,21
10,15,12,18,19,45,36,21
15,10,12,18,19,36,45,21
10,15,12,19,18,45,36,21
先从后往前扫描,比19小的与19交换
再从前往后扫描,比19大的与19交换
19,15,12,18 ,21,36,45,10 // 从后往前扫描 10比19小,交换
10,15,12,18 ,21,36,45,19 // 从前往后扫描 21比19大,交换
10,15,12,18 ,19,36,45,21 // 19前边都比19小,后边都比19大,一趟比较结束
官方给出的答案是
一个不断挖坑填坑的过程
按题意,先把a[0]挖坑,然后从tail开始找第一个小于pivot的值
这里是a[7]=10
把10填到之前的那个坑中
同时a[7]变成一个坑
再从前往后
找到第一个大于pivot的值a[4]=21
用21填之前的那个坑
并在a[4]挖个坑
再从a[6]开始向前寻找第一个小于pivot的值
然后没找到
把pivot填进那个坑就得到最终结果
pivot = 19
[],15,12,18,21,36,45,10
10,15,12,18,21,36,45,[]
10,15,12,18,[],36,45,21
最后填坑
10,15,12,18,19,36,45,21
*/
排序方法时间复杂度
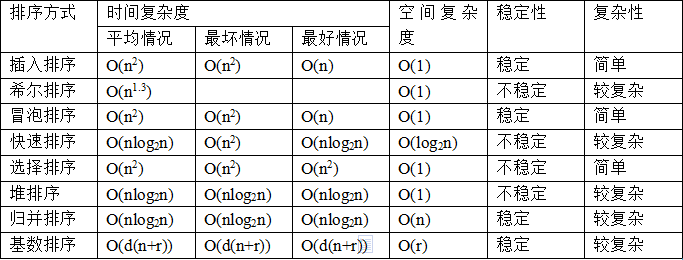




 本文详细探讨了排序算法中的归并排序和快速排序,包括二路归并排序的过程、归并排序相对于快速排序的优势、hash表排序的应用、拓扑排序序列的构建,以及快速排序在特定场景下的高效性。同时,还分析了不同排序方法的时间复杂度,为读者提供了全面的排序算法理解。
本文详细探讨了排序算法中的归并排序和快速排序,包括二路归并排序的过程、归并排序相对于快速排序的优势、hash表排序的应用、拓扑排序序列的构建,以及快速排序在特定场景下的高效性。同时,还分析了不同排序方法的时间复杂度,为读者提供了全面的排序算法理解。

















 994
994

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










