混合整数分式规划问题的等价非分式形式

最近看了一篇文献，文献中经过一系列的理论推导，形成了一个混合整数分式规划问题，随后依据一个理论，得到了问题的等价非分式形式，在这一步中我没有看懂，依据的理论截图放在下面了。

这个定理我在csdn上搜索没有搜到，我打算去学习一下，并分享在这里。这个理论在Werner Dinkelbach在1967发表的文章On Nonlinear Fractional Programming中有提到。我看了一下这篇文章，里面有对这个定理较为详细的证明。但是证明过程对于我来说有些复杂，那我就退而求其次，尝试搞清楚这个定理他到底说了一件什么事情吧。以下只是我的大致感觉，十分不严谨，若有问题，欢迎讨论。 

1、问题的前提

我们有两个连续实值函数，和，自变量的定义域是，我们假设,我们需要考虑的是两个问题，如下：

问题1：

问题2：

原文献的一个引理中提到，，并且有唯一解，这个唯一解我们记作，此时取得最大值的那个记作

2、定理是啥意思

有了上面的铺垫，我们再来看看上面的定理到底说了啥。定理是说，在且仅在上述的处，得到我们问题1所求的最大值，并且这个最大值就是。再放一遍定理如下：

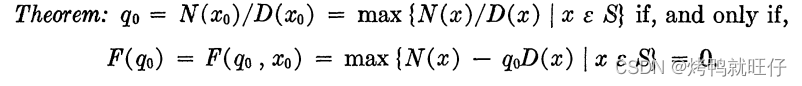
如果单从应用的角度来看的话，我的目的就是要将一个分式的最大值问题，也就是转化为它的等价非分式形式，那不就是求当q为何值时，，这样我的问题就解决了。