摘要:近十年来,基于向量节点表示的网络嵌入学习引起了广泛关注。它不同于图节点嵌入的一般设置,后者也会考虑节点属性,但可能会引发隐私问题。在本文中,我们脱离经典的 CPU/GPU 架构,考虑基于网络嵌入的成熟网络对齐问题,并开发一种低量子比特成本的量子机器学习方法,以便在不久的将来应用于嘈杂的中型量子 (NISQ) 设备。具体来说,我们的模型采用离散时间量子行走 (QW),并在定制的合并网络上进行 QW,以从两个对齐网络中提取结构信息,而无需量子态准备,否则需要高量子门成本。然后将 QW 中的量子态输入到量子嵌入 ansatz(即参数化电路)以学习每个节点的潜在表示。我们方法的关键部分是连接这两个量子模块以实现纯量子范式,而无需涉及经典模块。据我们所知,目前还没有任何经典-量子混合网络嵌入方法,更不用说摆脱经典设备和量子设备之间通信瓶颈的纯量子范式了,这仍然是一个悬而未决的问题。在两个真实数据集上的实验结果表明,与经典嵌入方法相比,我们的量子嵌入方法更有效。我们的模型可以用 Python 轻松高效地实现,并对 QW 和量子电路进行全幅度模拟。因此,我们的模型可以很容易地部署在现有的 NISQ 设备上,并提供所有电路,实验中只需要 13 个量子比特,这在现有的量子图学习工作中很少能达到。
方法
网络定义为 G = (V, E),其中 V 是节点集,E ⊆ V × V 是边集。给定源网络 Gs、目标网络 Gt 和锚链接 Ttrain ⊂ Vs × Vt,其中包含跨 Gs 和 Gt 的部分节点对齐,网络对齐旨在预测 Ttest 中未知的锚链接。我们开发了一个量子管道来学习顶点表示并对齐不同网络中的顶点。VQNE 的整体框架如下图所示。
量子游走
量子游走(QW)可以看作是经典随机游动的量子等价物,在量子算法中有着广泛的应用,例如量子游动搜索算法[35]、量子PageRanks[31]和量子模拟[30]。根据时间演化的类型,图上的量子游动分为连续时间[17]和离散时间量子游动[1]。在离散时间情况下,有两种常见模型:合成量子游动[2]和Szegedy量子游动[39]。合成量子游动基于图的顶点,更适合所有节点都具有相同度数的正则图。然而在网络对齐任务中,网络顶点通常具有不同数量的邻居。因此,本文我们选择基于图边的Szegedy量子游动来捕获网络信息。与经典随机游走相比,Szegedy 量子游走已被证明可以在量子命中时间上提供二次加速 [28]。首先,我们使用锚链接 Ttrain 将源网络 Gs 和目标网络 Gt 合并为网络 G。合并两个网络的详细过程可以在算法 1 中看到。对于合并后的图 G = (V, E),节点数为 N = |V |,我们可以定义一个 N 乘以 N 的邻接矩阵 A 为:

相关的过渡矩阵P被定义为:

其中 d j 是节点 v j 的入度,即。其次,我们在合并网络 G 上进行 Szegedy 量子行走 (SQW)。我们可以将 SQW 定义为希尔伯特空间
上的幺正运算。希尔伯特空间
上的量子态 |Ψ〉 可以写成叠加态:

其中 |i, j〉 表示当前 SQW 在顶点 i 处的状态,下一步将移动到顶点 j ,表示量子态 |i, j〉 的概率。我们首先定义马尔可夫链的投影状态 |ψi 〉 为:

到所张空间的投影算子为

以及相关的反射运算符 C = 2Π − I。然后我们需要一个交换运算符来交换两个寄存器

注意到 C 和 S 都满足幺正算子的定义。基于算子 S 和 Π,我们可以引入 SQW 的一个步骤:
![]()
量子行走:
![]()
这样,对于一个有 N 个节点的网络,我们可以用 n = ⌈log2 N ⌉ 个量子比特来表示 QW。对于顶点 vi ,我们可以得到一个 n 量子比特的量子编码态 |Ψt i 〉,它将作为接下来的量子嵌入假设的输入,以学习 vi 的潜在表示。
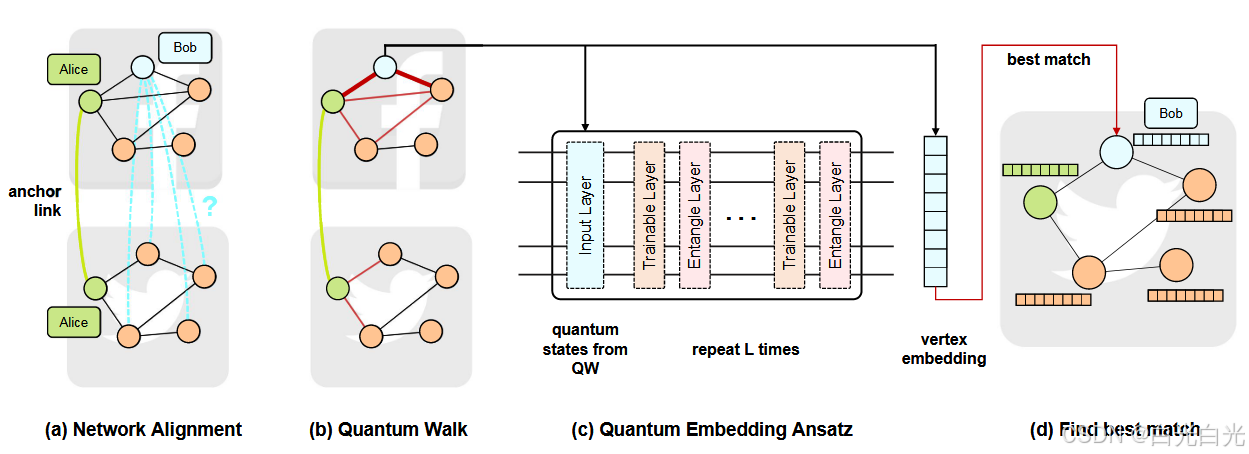
图 1:方法概述。(a)网络对齐的定义。对于具有锚链接 Alice 的两个社交网络 Facebook 和 Twitter,我们尝试在 Twitter 网络中找到 Bob 以将两个网络对齐在一起。(b)我们首先在网络上应用量子行走。粗红边是第一步,细红边是第二步。请注意,使用锚链接,我们可以跨网络行走。(c)量子嵌入假设。假设的输入是某一步骤的 QW 的状态向量。然后交替应用具有可训练参数的训练层和纠缠层来模拟经典的机器学习层。(d)我们计算 Bob-Facebook 和 Twitter 中所有顶点的嵌入之间的相似度,并将相似度最大的顶点作为 Bob-Twitter。
量子嵌入方法
如何构建参数量子电路来学习顶点的表示。硬件高效假设 (HEA) 是量子电路中最著名的假设之一。HEA 旨在使用本机门和本地连接来最小化量子硬件噪声的影响。[24] 的论文证明它在具有六个固定频率 transmon 量子比特的超导量子处理器上有效,[22] 的论文证明它在 56 量子比特超导量子处理器 祖冲之上有效。图 2(a) 说明了 HEA 的总体框架,它由两个主要模块组成:由单量子位门构成的可训练参数块 Ul 和由两个量子位门构成的纠缠块 Uent。Ul 和 Uent 的内部结构并不唯一,可以由用户自定义。在本文中,我们还选择 HEA 作为学习网络嵌入的主要可训练模块。图 2(b) 和 (c) 显示了本文设计的 Ul 和 Uent 块。可训练层Ul由一系列单量子比特参数化旋转门RzRyRz构成,纠缠层Uent由两个量子比特CNOT门组成,用于成对纠缠相邻的量子比特。我们简单讨论一下为什么在可训练层中使用的组合。任何单量子比特门U都可以分解为一组
和一个全局相位

图 2:(a) 硬件高效拟定 (HEA) 的总体架构。HEA 包含 L 层,每层包含由单量子位门构成的可训练参数块 Ul 和由双量子位门构成的纠缠块 Uent。(b) 我们的 VQNE 拟定的可训练参数块 Ul 的电路。三个具有不同参数 RzRyRz 的旋转门作用于每个量子位。电路中有 n 个量子位,因此每层有 3n 个可训练参数。(c) 我们的 VQNE 拟定的纠缠块 Uent 的电路。纠缠层由 CNOT 门组成,以成对纠缠两个相邻的量子位。请注意,我们认为最后一个量子位与第一个量子位相邻。

其中 Ul(θ) 是第 l 个可训练层,其定义为:
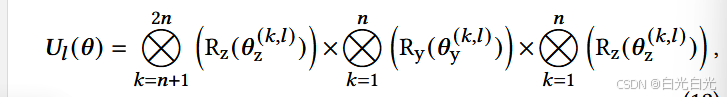
其中 θ (k,l ) 和 θ (k,l ) 是第 l 层第 k 个量子比特上 Rz 和 Ry 的可训练参数。对于每个 vi ∈ V,量子行走输出量子态 |Ψt i 〉 作为量子嵌入假设的输入 |Ψi (0)〉。经过 L 层 HEA 后,量子态变为

它被用作顶点 vi 的嵌入向量。
VQNE 的训练和测试
与 一致,我们使用边际三元组 (MT) 目标 和负采样进行训练,与网络嵌入和对比学习中其他广泛使用的目标(例如 NT-Logistics )相比,它在网络对齐任务中通过实验表现出更好的性能。MT 损失为:

其中 xi 是节点 vi 的嵌入,γ 是一个超参数,表示正样本和负样本之间的边际。正样本对由 (xi, xj ) 给出,其中 xj 表示 xi 的嵌入向量。负样本对为 (xi, xj′ ),Pneg 是负样本的分布,我们使用均匀分布。我们进一步采用 [45] 中引入的弹性势能函数进行稳健的嵌入学习,其形式为:

那么最终目标就变成
![]()
其中 η 表示 QEPE 在总目标中的权重。训练和测试细节在算法 2 中给出。我们首先根据锚链接合并两个网络,然后在合并网络的每个节点上进行量子行走。通过这种方式,执行量子行走可以捕获两个网络的信息。经过 t 步量子行走后,我们得到顶点 vi 的量子态 |Ψt i 〉。得到的量子态 |Ψt i 〉 作为量子拟设的输入,然后拟设输出 vi 的嵌入向量。在训练阶段,由于我们使用了边际三重态损失,我们首先需要抽取正实例和负实例。正样本对由 vi 的嵌入向量和 vi 的嵌入向量组成。负样本是在网络 G 中随机选择的。拟设的参数 θ s 通过移位技术计算出的梯度进行更新。整个训练过程重复 iter _num 次,以确保所有 θ 都得到适当训练。训练过程结束后,我们使用 Ttest 中的所有顶点测试模型的精度,然后应用评估指标 precision@K。两个顶点之间的相似性通过其嵌入向量的内积来计算。
关于公式的推导:
引理 A.1. 任意一个以酉矩阵为 U 的单量子比特算子都可以分解为一系列 Rz、Ry 和 Rz 门,以及一个全局相位
定理A.2. 任何单量子比特量子门U都可以分解为一组RzRyRz和相移门。
什么是网络对齐?
网络对齐(Network Alignment)是指将两个或多个网络中相同或相似的节点进行匹配或对齐的过程。它涉及到在多个网络之间找出相同或相似节点的对应关系。
为了更好的理解网络对齐的实际意义,举例如下。
1. 跨域推荐系统
在电商平台、社交媒体或内容平台上,用户在不同平台上的行为可能存在重叠。例如,一个用户在亚马逊购物平台上可能会购买某些商品,而在推特上也可能对某些商品进行评论。为了提高推荐系统的精度,需要将来自不同平台的数据进行对齐,找到这些平台上相同或相似的用户。网络对齐可以通过识别和对齐这些用户,从而为推荐系统提供更准确的建议。
- 实例:用户在不同电商网站上的购买行为数据被视作两个不同的网络,通过网络对齐可以找到不同平台上的相同用户,并将其行为信息整合,以提供更个性化的推荐。
2. 多维社交网络分析
社交网络的对齐是另一个重要的应用场景。在现代社会,用户可能在多个社交平台(如Facebook、Twitter、LinkedIn等)上活跃,每个平台的社交网络结构是不同的。通过对齐不同社交平台上的用户和互动关系,可以帮助研究人员或企业了解用户跨平台的行为模式和兴趣,从而改善用户体验或制定营销策略。
- 实例:假设一个企业希望了解其在Facebook和Twitter上的用户互动情况,网络对齐可以帮助将两个平台上的用户关联起来,进一步分析这些用户在不同平台上的行为差异。
3. 生物信息学中的基因网络对齐
在生物学领域,基因或蛋白质相互作用网络(PPI网络)可以帮助研究人员理解基因之间的关系。由于不同物种的基因组信息不同,科学家需要对比多个物种的基因相互作用网络。通过网络对齐,可以找出不同物种中相同或相似的基因,从而揭示它们在不同物种中的相似性或进化关系。
- 实例:通过对比人类和小鼠的基因相互作用网络,科学家可以找到两者之间的相似基因,并利用这些信息来研究某些疾病的遗传机制或药物的潜在疗效。
4. 知识图谱的跨语言对齐
知识图谱(Knowledge Graph)是一种将信息表示为节点和边的图结构。在全球范围内,不同语言的知识图谱可能包含相同的实体和关系,但它们的表示和语言结构不同。通过网络对齐,可以将不同语言中的知识图谱进行对齐,从而跨语言地整合信息。
- 实例:一个英文维基百科的知识图谱与中文维基百科的知识图谱可能包含相同的实体,如“爱因斯坦”。通过对齐,可以将这两个不同语言中的“爱因斯坦”实体关联起来,帮助建立一个多语言支持的知识图谱。
5. 金融诈骗检测
在金融网络中,不同的金融机构之间存在资金流动和交易行为。当涉及到金融诈骗或洗钱行为时,这些行为可能跨越不同的金融机构或国家,形成多层次的网络。通过对齐不同金融网络中的交易记录和参与者,可以帮助识别跨机构或跨国的金融诈骗活动。
- 实例:通过对齐不同银行之间的交易网络,可以揭示资金流动的异常模式,帮助发现潜在的洗钱活动。
如何解释公式?

注意小于1,
表示反射幅度,决定了该量子态从 iii 到 jjj 的回跳概率。叠加是指量子行走者(即量子粒子)可以同时处于多个位置(即多个节点)上。量子干涉效应是量子力学中又一个非常重要的概念,指的是量子态之间相互作用和叠加导致的概率幅度变化。当量子系统处于多个可能的路径(即多个叠加态)时,这些路径会相互干涉,导致一些路径的概率增强,而其他路径的概率减弱。




附录
1.为什么要对齐网络?
网络对齐(Network Alignment)是指将两个或多个网络中相同或相似的节点进行匹配或对齐的过程。对齐的目标是找到源网络(Gs)和目标网络(Gt)中节点之间的相似性或关系,并且通常用于以下几个方面:
-
跨网络的节点映射:当两个网络的节点表示不同的信息时,网络对齐有助于识别这些节点之间的相似性。例如,在社交网络中,两个社交平台的用户节点可能是不同的,但他们可能代表的是同一个人或者具有相似的属性和行为。
-
跨域任务:在跨域任务中,不同的网络通常会有不同的结构和属性。网络对齐可以帮助识别节点和边的相似性,从而使跨网络的任务更加有效。
-
提高信息共享和推理能力:对齐后的网络使得信息可以在不同的网络之间流动,从而在一个网络中的信息可以应用到另一个网络。这对于许多实际问题,如推荐系统、知识图谱、疾病预测等都非常有帮助。
-
节点间隐含关系的发现:在某些应用中,两个网络可能有部分已知的节点对齐(称为锚点对齐),对齐的目标是发现那些尚未对齐的节点对,从而实现更多的信息共享和推理。
在你的问题中,VQNE的目标就是通过量子计算的方式来进行网络对齐,特别是在源网络(Gs)和目标网络(Gt)之间进行节点对齐,从而预测未知的锚点链接(Ttest)。
2.什么是pipeline?
在机器学习和量子计算的上下文中,pipeline(管道) 是指一系列连续的处理步骤,每个步骤都将数据从一个阶段传递到下一个阶段。在VQNE的背景下,pipeline指的是以下几个处理步骤:
-
图的合并:将源网络(Gs)和目标网络(Gt)合并为一个大网络,其中的锚点对链接(Ttrain)连接了两个网络。每个锚点对链接将源网络和目标网络中的节点合并,从而使得量子行走(Quantum Walk)可以在两个网络之间移动。
-
离散时间量子行走(Discrete-Time Quantum Walk):合并后的网络通过量子行走来编码节点的拓扑信息。量子行走模拟了量子粒子在图中的运动,其中量子态的叠加表示了节点的拓扑结构。
-
量子嵌入(Quantum Embedding):量子行走的结果是一个量子态,它表示了每个节点的潜在特征。这些量子态然后通过量子嵌入层进行处理,学习节点的潜在表示。
-
相似性计算和匹配:通过计算不同节点之间的相似性来找到最佳匹配,进而预测未知的锚点链接(Ttest)。这通常是通过在量子嵌入层中学习到的节点表示来完成的。
-
最终输出:最终的目标是通过量子处理得到一个潜在的节点表示,并根据这些表示预测未知的链接。
3.反射幅度是什么?
反射幅度(Reflection Amplitude)是量子行走中的一个关键概念,它描述了量子态与某个特定状态之间的反射过程。在量子行走的过程中,当粒子(在这里是量子行走者)从一个节点移动到另一个节点时,它可以遇到 反射,即它可能“返回”到原来的节点或在其它方向上改变其运动轨迹。这一反射过程与经典行走的路径不同,因为量子行走不仅包含正常的传播,还涉及到量子干涉和叠加。
1. 反射的数学表示
在量子行走中,反射幅度通常表示为量子态的 相位变化,它通常用于在量子图行走中描述从一个节点到另一个节点的反向运动。例如,在 Szedegy 量子行走中,反射幅度被引入来调整量子态的传播方向,使得量子行走过程不仅是单向传播,还包含反射的效果。
反射幅度通常与 邻接矩阵 或 入度(或出度)等图的拓扑属性相关。在图中某个节点的反射幅度反映了该节点的结构特性和量子态传播的概率。
2. 反射幅度在量子行走中的作用
反射幅度的引入有以下几个重要作用:
-
保持概率归一性: 在量子行走中,反射幅度有助于保持总的量子概率幅度的归一性,即所有的量子态的总和应该等于 1。反射不仅帮助量子行走在图中传播,还通过控制反射幅度来确保系统的量子态在传播过程中不发生信息的丢失或不一致。
-
增强量子干涉效应: 反射幅度在量子行走中的引入可以加强量子干涉效应。量子行走的一个重要特点是干涉现象——不同路径的量子态会相互干涉,导致最终的结果(例如,概率分布)与经典的随机行走完全不同。反射幅度的控制有助于调节这些干涉效应,优化量子行走的表现。
-
控制量子行走的方向性: 在图的量子行走过程中,反射幅度帮助控制行走者在节点之间的转移方向。例如,在经典的随机行走中,行走者可以选择均匀地向任何相邻节点移动;而在量子行走中,反射幅度决定了在特定节点的反射行为,可以影响量子态的传播方向。这种反射行为对量子行走的速度、稳定性和搜索效果非常关键。
























 1293
1293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










