并查集（入门算法基础讲解1）

本人也是学习了一段时间后，在了解并查集基本算法的情况下去力扣刷题发现有些部分完全不够看，在相应网站（百度，优快云，知乎……）查找对应资料也是没有找到令人满意的资料，后面也是自己想了很久才解决，现在在这里和大家分享一下。

首先我们先来介绍一下并查集算法吧

并查集：一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（union-find algorithm）定义了两个用于此数据结构的操作：

Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。（百度上的介绍）

上面已经说的很清楚了，用于不相交的合并及查询问题，并查集怎么去记忆那，顾名思义，并就是“和”的意思，查就是“查找（find）”的意思，集就是“集合，合并（union）的意思”，就是实现“查找”与“合并”的操作，所以叫做并查集

上面大致介绍后，我们来通过编程的形式再来走一遍（理论再多，抵不过实践出真知）

实际上并查集还包括一个初始化（init）的过程，因为一开始的时候没有存在任何关系，所以是需要自己指向自己的

并查集第一部分

init

我们需要定义一个一维数组，让一开始指向自己，即array[i]=i;

如图：

 当然数组不是乱定义，根据题目，题目中有几个不同的对象，一维数组就定义多大

并查集第二部分

find

在这里我们需要做的事寻找每一个对象的祖先，举个例子，一开始array[1]不和任何元素有关，所以array[1]=1;此刻元素的值就是它祖先的下标也就是它自己，如果，array[1]和array[2]有关系，一开始array[1]=1;array[2]=2,此刻我们就可以让array[1]=2或者array[2]=1,让元素的值就是它祖先的下标,我们find要做的操作就是去查找这个祖先的下标或者说是值，因为初始array[i]=i;

 在这里这种写法基本可以满足我们查找的要求，但是有一个问题，那就是假如传入的k它前面有很多（也可以说是有很多它的长辈），而且我们每次查k的祖先都要一层，一层的查，这样存在冗余计算，浪费时间，增加时间复杂度

因此我们需要改进

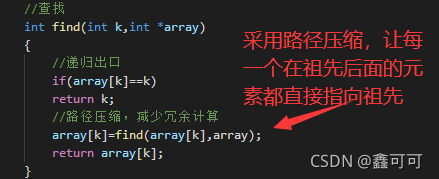
 这样我们就避免了如果多次查同一个k的祖先，都需要从头查，现在可以跳过很多操作过的步骤

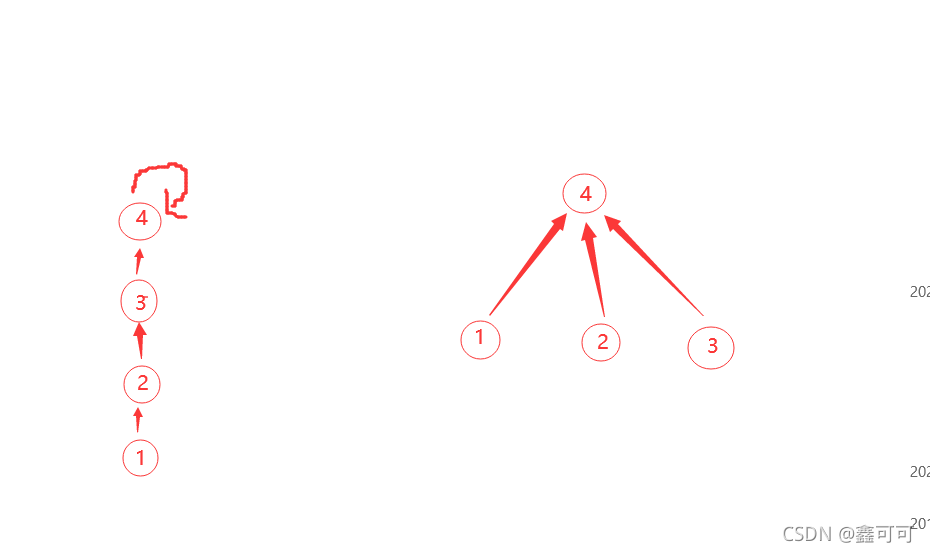
左边就是没有优化前的find,对次查找1的祖先，都会一层层查找，冗余计算了

右边是优化后的find,查找1的祖先只需要走一次一层层查找，后面直接指向祖先，不会再有冗余计算

 并查集第三部分

union

如果两个元素存在关系，我们需要将他们连在一起，

一个祖先指向另一个其实也就是让一个祖先的数组里的值更新为另一个祖先的数组下标，这样前一个祖先相当于后一个祖先的儿子（哈哈哈哈），然后就实现了联合

至此并查集的三个部分全部介绍完；

完整代码如下

整体介绍完之后，我们来做几个题吧

例题1：

本题目来自bilibili麦克老师视屏讲解中的一个题目

就是说先给你一串关系，然后再随便给你两个人物，让你判断他们是否有关系

这就是一个最基础的并查集问题，先通过并查集将有关系的人进行联合，然后通过查找这两个人的祖先，如果有相同祖先则是有关系，否则无关

代码如下

 大家可以自己去练习一下，印象更深刻

例题2：力扣题号547.省份数量

 代码如下

 到此为止，如果大家细心阅读，并且动手实践，我相信一维数组的并查集求不同区域数量或者两者之间的关系什么的，对大家来说都是比较简单的了。今天太晚了

后面更新二维数组的并查集做法