【AI安全之对抗样本】深度学习基础知识（一）

最新推荐文章于 2025-04-14 16:42:14 发布

吃_早餐

最新推荐文章于 2025-04-14 16:42:14 发布

阅读量1.4k

点赞数

分类专栏： AI安全之对抗样本文章标签：人工智能安全深度学习

本文链接：https://blog.youkuaiyun.com/m0_52923241/article/details/123169090

版权

AI安全之对抗样本专栏收录该内容

3 篇文章

订阅专栏

文章目录

00 前言
01 深度学习的基本过程及相关概念
03 总结

00 前言

【我的AI安全之路】以下内容适合于有web安全基础但对AI"一无所知"的师傅们

如果是有安全基础，想入门AI安全，可以看下以web安全为背景介绍AI安全的书：《Web安全之机器学习入门》和《Web安全之深度学习实战》，以及一本关于对抗样本的书：《AI安全之对抗样本入门》

【补充】以下均基于深度学习主流框架之一keras为例

01 深度学习的基本过程及相关概念

1.1 深度学习的基本过程

深度学习主要包括训练和预测两个过程。

训练过程：使用预先定义好的网络结构，在有标记的数据上进行训练，然后通过一定的算法不断调整网络的参数，是结果满足一定的要求。
预测过程：使用训练好的模型，对数据进行运算，并获得预测结果。

1.2 数据预处理

数据预处理就是把物理世界中的实物特征化，最终表示为多维向量的过程。

Eg：图片可以表示为多维向量，使用长度，宽度，信道数表示图片的形状。

分辨率为10×10的灰度图像→形状为[10,10,1]的向量

分辨率为10×10的RGB图像→形状为[10,10,3]的向量

1.3 网络结构

完整的训练好的深度学习模型 = 对网络结构的描述(or对网络结构的定义) + 每层网络的具体参数

定义网络是的常用层包括一下几层

其中，keras框架中的常用层的函数包含在keras.layers.core中

1.3.1 Dense层（全连接层）

作用：用于构建一个全连接。
全连接结构包括：输入、求和、激活、权重矩阵、偏置、输出。（从此角度来说，训练的过程就是获得最优的权重矩阵和偏置的过程）

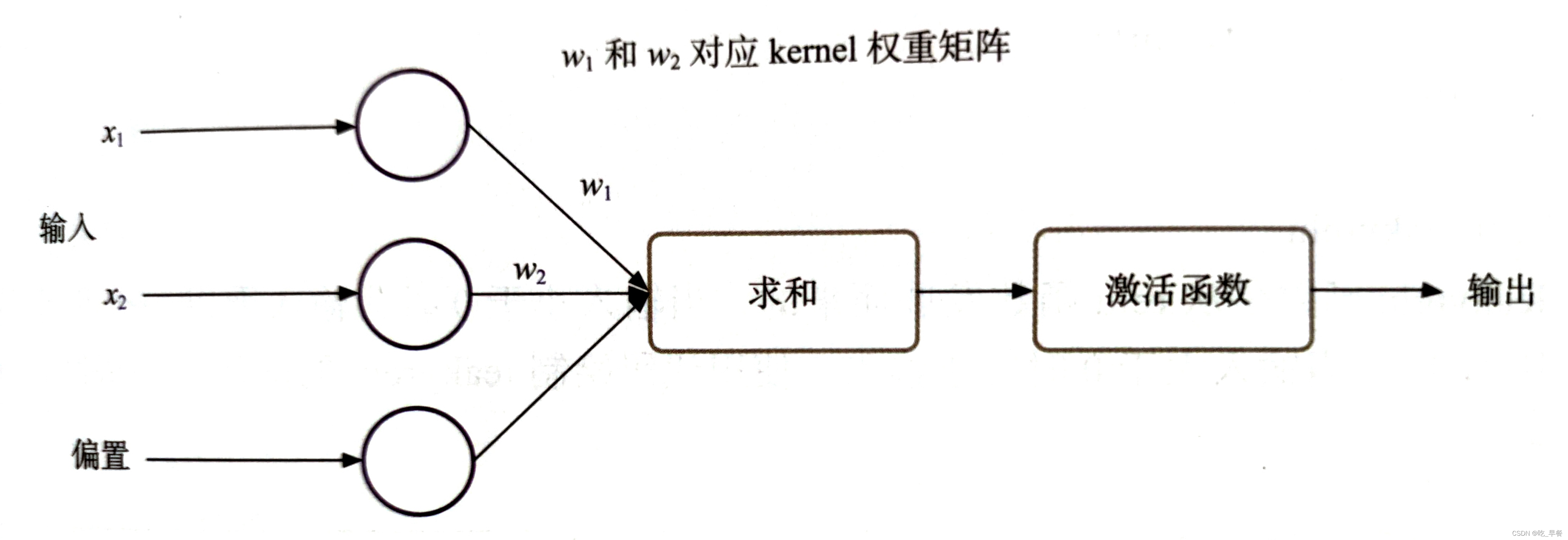
在这里插入图片描述

【补充知识点】

在y=WX+b中，W是权重矩阵，b是偏置

定义Dense层

keras.layers.core.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)
以上定义中重要的几个参数

units：隐藏层节点数（空间的维数）

activation：激活函数（详细见1.3.2 Activation层）

use_bias：是否使用偏置

kernel_initializer='glorot_uniform'：核权重矩阵的初始值设定项

bias_initializer='zeros'：偏差向量的初始值设定项

kernel_regularizer=None：正则化函数应用于核权矩阵

bias_regularizer=None：应用于偏差向量的正则化函数

kernel_constraint=None：对权重矩阵约束

bias_constraint=None：对偏置向量约束

1.3.2 Activation层（激活层）

作用：对一个层的输出施加激活函数
补充：该层可以单独使用，也可以作为其它层的参数（例如做Dense层的参数）

激活函数

①relu

当输入小于0时为0，当输入大于0是为输入

函数公式为：
$f(x)=max(0, x)=\left{\begin{matrix} 0 & (x \leqslant 0)& \ x & (x > 0) & \end{matrix}\right.$
在这里插入图片描述

图像代码如下：

def relu(X):
	if x > 0:
        return x
    else:
    	return 0
def func4():	
    x = np.arange(-5.0, 5.0, 0.02)#返回一个终点为5.0，起点为-5.0，固定步长为0.02的排列
    y = []
    for i in x:
        yi = relu(x)
        y.append(yi)
    plt.xlabel('x')				#设置x轴的标签文本
    plt.ylabel('y relu(x)')		#设置y轴的标签文本
    plt.title('relu')			#设置图像标题
    plt.plot(x, y)				#展现变量的趋势变化。
    plt.show()					#画出图像

【补充知识点】

np.arange()函数返回一个有终点和起点的固定步长的排列
参数个数情况： np.arange()函数分为一个参数，两个参数，三个参数三种情况
1）一个参数时，参数值为终点，起点取默认值0，步长取默认值1。
2）两个参数时，第一个参数为起点，第二个参数为终点，步长取默认值1。
3）三个参数时，第一个参数为起点，第二个参数为终点，第三个参数为步长。其中步长支持小数
append()函数表示在列表末尾添加新的对象

②leakyrelu

当输入小于0时乘以一个很小的系数，当输入大于0是为输入
在这里插入图片描述

图像代码如下：

def relu(X):
	if x > 0:
        return x
    else:
    	return x * 0.1
def func4():	
    x = np.arange(-5.0, 5.0, 0.02)#返回一个终点为5.0，起点为-5.0，固定步长为0.02的排列
    y = []
    for i in x:
        yi = relu(x)
        y.append(yi)
    plt.xlabel('x')					#设置x轴的标签文本
    plt.ylabel('y leakyrelu(x)')	#设置y轴的标签文本
    plt.title('leakyrelu')			#设置图像标题
    plt.plot(x, y)					#展现变量的趋势变化。
    plt.show()						#画出图像

③tanh

双切正切函数，取值范围为[-1,1]

函数公式为
在这里插入图片描述

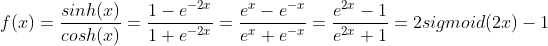
图像代码如下

x = np.arange(-5.0, 5.0, 0.02)
y = (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
plt.xlabel('x')					
plt.ylabel('y tanh(x)')	
plt.title('tanh')
plt.plot(x, y)					
plt.show()

④sigmoid

将一个实数映射到（0,1）区间，可用于做二分类

函数公式为
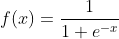
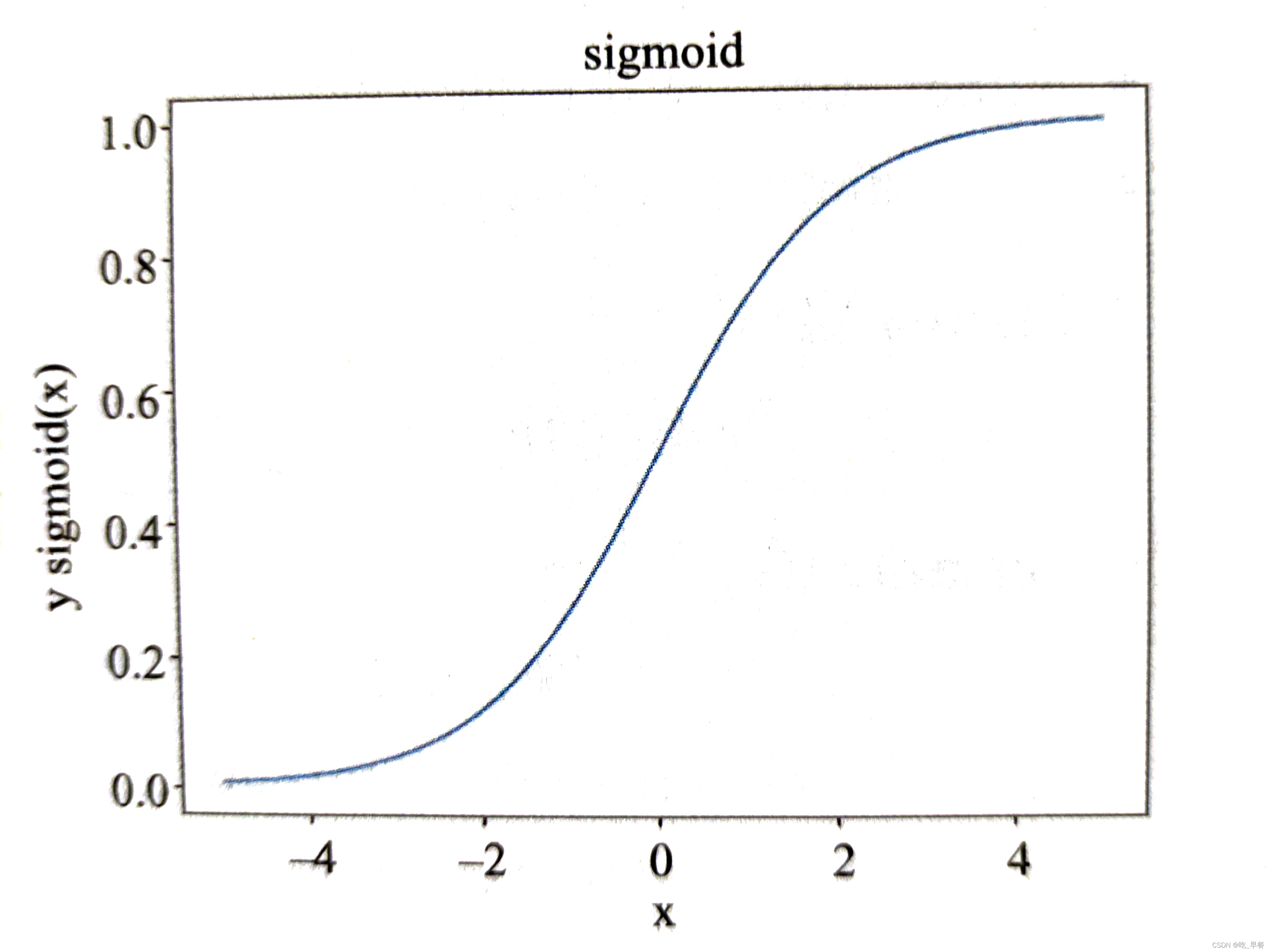在这里插入图片描述图像代码如下

x = np.arange(-5.0, 5.0, 0.02)
y = i / (1 + np.exp(-x))
plt.xlabel('x')					
plt.ylabel('y sigmoid(x)')	
plt.title('sigmoid')
plt.plot(x, y)					
plt.show()

基本的model搭建

Eg：创建一个输入大小为784，节点数（空间维数）为32，激活函数为relu的全连接层的代码

model.add(Dense(32, activation='rule', input_shape=(784,)))

1.3.3 Dropout层（随机失活层）

作用：为避免过拟合，在训练时随机选择一定的结点临时失效（识别图像是随机挡住一些像素不会影响图片的识别）

【补充知识点】

过拟合：包含参数过多，对已知数据预测的很好，对未知预测的很差（对预测过度严格）
定义Dropout层

teras.layers.core.Dropout(rate,noise_shape=None,seed=None)

其中rate表示临时失效的节点比例（经验值为0.2~0.4比较合适）

1.3.4 Embedding层（嵌入层）

作用：将输入的向量按照一定的规则改变维度
定义Embedding层

keras.layers.Embedding(input_dim, output_dim, embeddings_initializer='uniform', embeddings_regularizer=None, activity_regularizer=None, embeddings_constraint=None, mask_zero=False, input_length=None）
以上定义中重要的几个参数

input_dim：输入的向量的维度

output_dim：输出的向量的维度

embeddings_initializer：初始化的方式，通常使用glorot_normal或者uniform

1.3.5 Flatten层

作用：把多维的输入一维化

1.3.6 Permute层

作用：将输入的维度按照指定模式进行重排
Permute层重排代码：
```
if K.image_dim_ordering() == 'tf':
    model.add(Permute((2,3,1), input_shape=input_shape))
elif K.image_dim_ordering() == 'th':
    model.add(Permute((1,2,3), input_shape=input_shape))
else:
    raise RuntimeError('Unknoen image_dim_ordering.')
```
【补充知识点】
- 深度学习主流框架：
  - 框架名称：TensorFlow
  - 主要维护方：Google
  - 支持的语言：C++/Python/Java/R 等
  - GitHub源码地址：https://github.com/tensorflow/tensorflow
  - 框架名称：Keras
  - 主要维护方：Google
  - 支持的语言：Python/R
  - GitHub源码地址：https://github.com/keras-team/keras
  - 框架名称：Caffe
  - 主要维护方：BVLC
  - 支持的语言：C++/Python/Matlab
  - GitHub源码地址：https://github.com/BVLC/caffe
  - 框架名称：PyTorch
  - 主要维护方：Facebook
  - 支持的语言：C/C++/Python
  - GitHub源码地址：https://github.com/pytorch/pytorch
  - 框架名称：Theano
  - 主要维护方：UdeM
  - 支持的语言：Python
  - GitHub源码地址：https://github.com/Theano/Theano
  - 框架名称：CNTK
  - 主要维护方：Microsoft
  - 支持的语言：C++/Python/C#/.NET/Java/R
  - GitHub源码地址：https://github.com/Microsoft/CNTK
  - 框架名称：MXNet
  - 主要维护方：DMLC
  - 支持的语言：C++/Python/R等
  - GitHub源码地址：https://github.com/apache/incubator-mxnet
  - 框架名称：PaddlePaddle
  - 主要维护方：Baidu
  - 支持的语言：C++/Python
  - GitHub源码地址：https://github.com/PaddlePaddle/Paddle/
  - 框架名称：Deeplearning4j
  - 主要维护方：Eclipse
  - 支持的语言：Java/Scala等
  - GitHub源码地址：https://github.com/eclipse/deeplearning4j
  - 框架名称：ONNX
  - 主要维护方：Microsoft/ Facebook
  - 支持的语言：Python/R
  - GitHub源码地址：https://github.com/onnx/onnx
- 这里具体了解一下TensorFlow和Theano的区别：
  
  TensorFlow图像保存的顺序是（width，height，channels）
  
  Theano图像保存的顺序是（channels，width，height）

1.3.7 Reshape 层

作用：将输入的shape转化为特定的shape
定义Reshape层

keras.layers.core.Reshape(target_shape)
以上定义中重要的几个参数

target_shape为希望转换成的形状

1.4 损失函数

Keras中常见的损失函数

mean_squared_error 或 mse （回归问题经常使用）
mean_absolute_error 或 mae （回归问题经常使用）
mean_absolute_percentage_error 或 mape 
mean_squared_logarithmic_error 或 msle 
squared_hinge 
hinge 
categorical_hinge 
binary_crossentropy （二分类问题经常使用）
logcosh 
categorical_crossentropy （多分类问题经常使用）
sparse_categorical_crossentrop