文章目录
堆
(1)堆描述
- (最大)堆:
- 是一个可以被看成一棵树的数组对象,满足如下性质:
- 堆中的父亲结点优先级总大于等于其左右孩子结点的值
- 总是一棵完全二叉树
- 可以把数字大的看做优先级高的,也可以把数字小的看做优先级低的
- 是一个可以被看成一棵树的数组对象,满足如下性质:
- 满二叉树:
- 每一层的节点树都为2^(h-1)
- 每一层都是满的
- 完全二叉树
- 叶子结点只能出现在最下层和次下层,且最下层的叶子结点集中在树的左部。
- 满二叉树肯定是完全二叉树,而完全二叉树不一定是满二叉树。
- 堆的性质
- 根节点没有父亲结点
- 除根节点之外的任意结点(i)的父亲结点的索引为: parent = i/2
- 任意结点的左孩子结点的索引为: leftIndex = 2 * i
- 任意结点的右孩子结点的索引为: rightIndex = 2 * i +1
- 上面的结论是根结点存储在索引为1的位置,如果根结点存储在索引为0的位置时,会得到.
(2)堆实现
1.创建堆
- 我们写的是二叉树堆,所以需要比较,就需要集成Comparable来实现
public class MaxHeap<K extends Comparable<K>> {
}
2.堆的初始化与构造方法
- 堆的底层为数组
- 第一个无参构造方法,初始化堆
- 元素为0,长度为100;方便后续进行添加操作
- 第二个有参构造方法
- 传参,传一个数组,可以将任一数组转换为堆的方式存储
- 判断堆的长度
- 判断堆是否为空
private K[] data;//堆底层的数据结构
private int size;//堆中元素个数
public MaxHeap() {
this.size = 0;
this.data = (K[]) new Comparable[100];
}
public MaxHeap(K[] arr) {
this.data = Arrays.copyOf(arr, arr.length);
this.size = arr.length;
}
//堆是否为空
public boolean isEmpty() {
return size == 0;
}
//获取堆的大小
public int getSize() {
return size;
}
3.堆的上浮
- 也就是向堆中添加元素
- 添加到数组中索引为size的位置,然后更新size
- 从最后一个结点开始与父亲结节进行(优先级)比较,如果父亲结点的优先级低于当前结点则进行交换
- 重复上述操作
- 直至根节点或父亲结点的优先级高于当前结点
- 每次添加都必须做一个维护,也就是上浮操作
- 目的是保证堆的特性:堆中的父亲结点优先级总大于等于其左右孩子结点的值
- 从索引为index的位置进行上浮操作,共有俩种方式
- 方式一:
- 将添加的节点定义为当前节点,找到其父亲节点
- 在判断索引为当前节点的值是否大于父亲节点的值
- 若大于则将俩个节点进行交换,并且索引同样进行交换
- 若小于等于,则跳出循环
- 方式二:
- 将添加的节点定义为当前节点,找到其父亲节点
- 在判断索引为当前节点的值是否大于父亲节点的值
- 若大于则将俩个节点的值进行交换,并且索引同样进行交换
- 若小于等于,则跳出循环
- 最后在将值付给当前节点
- 也可以说一个是更换节点,一个是只换节点的值
- 方式一:
- 时间复杂度:
- 最坏的情况是从size-1,每次查找父亲结点,每次上一层,直到根结点
- 即O(h)=O(logn)
- 若以添加方式讲数组转化为堆排序时,即n个元素O(nh)
- 时间负责度为O(nlogn)
//向堆中添加元素
public void add(K ele) {
//添加到索引为size的位置,维护size
data[size] = ele;
size++;
//维护最大堆的性质,进行上浮操作,从最后一个元素开始
floatup(size - 1);
}
//从索引为index的位置进行上浮操作
public void floatup(int index) {
int curIndex = index;//当前结点
int parentIndex = (index - 1) / 2;
while (curIndex > 0 && data[parentIndex].compareTo(data[curIndex]) < 0) {
swap(parentIndex, curIndex);
curIndex = parentIndex;
parentIndex = (curIndex - 1) / 2;
}
}
//从索引为index的位置进行上浮操作 方式二
public void floatup2(int index, K ele) {
int curIndex = index;//当前结点
int parentIndex = (index - 1) / 2;
while (curIndex > 0 && data[parentIndex].compareTo(data[curIndex]) < 0) {
data[curIndex] = data[parentIndex];
curIndex = parentIndex;
parentIndex = (curIndex - 1) / 2;
}
data[curIndex] = ele;
}
//交换方法
public void swap(int index1, int index2) {
K temp = data[index1];
data[index1] = data[index2];
data[index2] = temp;
}
4.堆的下沉
- 找到最大堆中优先级最高的元素也就是索引为0的元素
- 使用最后一个元素替换索引为0元素,size在减一,就自动舍去最后一个元素
- 从索引为0的位置开始进行下沉操作
- 将索引为0的节点定义为当前节点,找到其左子节点,右子节点即为左子节点加一
- 找到当前结点左右孩子结点中优先级较高的结点,
- 如果当前结点的优先级小于左右孩子结点中优先较高的结点,则进行交换
- 重复上述操作
- 直至叶子结点或左右孩子结点中优先级较高结点小于当前结点的优先级
- 时间复杂度:
- 最坏的情况是从索引为0开始,每次查找子结点,每次下一层,直到优先级最低的结点
- 即O(h)=O(logn)
//从堆中取出优先级最高的元素 下沉操作
public K removePriorityEle() {
if (isEmpty()) {
new IllegalArgumentException("heap is empty!");
}
//找到当前结点优先级最高的结点root
K ele = data[0];
data[0] = data[size - 1];
size--;
//进行下沉操作
siftDown();
return ele;
}
//从索引为index的位置进行下沉操作
private void siftDown() {
int curIndex = 0;
int leftIndex = 2 * curIndex + 1;
int changIndex = leftIndex;//要交换的结点,默认让他等于changeIndex
while (leftIndex < size) {
if (leftIndex + 1 < size && data[leftIndex].compareTo(data[leftIndex + 1]) < 0) {
changIndex = leftIndex + 1;
}
if (data[curIndex].compareTo(data[changIndex]) < 0) {
swap(curIndex, changIndex);
curIndex = changIndex;
leftIndex = 2 * curIndex + 1;
changIndex = leftIndex;
} else {
break;
}
}
}
5.测试使用添加的方法进行堆排序
public static void main(String[] args) {
test1();
//test2();
}
public static void test1() {
Integer[] arr = {62, 41, 30, 28, 16, 22, 17, 29, 19, 15, 67};
MaxHeap<Integer> heap = new MaxHeap<>();
Stream.of(arr).forEach(item -> {
heap.add(item);
});
System.out.println(heap.toString());
heap.replace(100);
System.out.println("--------------------------");
System.out.println(heap.toString());
}

6.replace操作与heapify操作
- replace操作 取出最大元素后,放入一个新元素
- 思想很简单,就是根节点的值替换成新的值,在进行下沉操作,使其维护成功
- heapify操作 将任意数组整理成堆的形状
- 就是数组的堆排序,从最后一个元素的父亲结点开始进行调整(sift down),直到根结点找到最后一个元素的父亲结点。 (size-1-1)/2
- 循环进行下沉操作,直至根结点也完成最后的下沉操作
- 注:
- 这里一定是size-1-1,因为size才是最后一个节点的索引,在根据上述所描述的也就是最后一个节点的索引-1在除以2就是父亲节点的索引
- 时间复杂度:
- 假设一棵完全二叉树的高度为h,最后一个结点的父亲结点一定在h-1层,从h-1层开始进行下沉操作,假设该层所有结点都要进行交换,那么每个结点交换的次数为1,所以总共交换了12次依次类推假设h − 2层的结点都要进行交换,每个结点最多交换2次,总共交换的次数为22 …到根节点交换的次数为 (h − 1) ∗ 2.
- 所以其时间复杂度为O(2^h) 即O(2^(logn))即O(n)
//replace操作 取出最大元素后,放入一个新元素
public void replace(K newValue) {
if (isEmpty()) {
new IllegalArgumentException("heap is empty!");
}
data[0] = newValue;
siftDown();
}
//heapify操作 将任意数组整理成堆的形状
public void heapify() {
if (this.data == null || this.data.length == 0) {
new IllegalArgumentException("Arr is null!");
}
int curIndex = (size - 1 - 1) / 2;//最后一个节点的父亲结点
for (; curIndex >= 0; curIndex--) {
siftDown(curIndex);
}
}
//从索引为index的位置进行下沉操作
private void siftDown(int curIndex) {
int leftIndex = 2 * curIndex + 1;
int changIndex = leftIndex;//要交换的结点,默认让他等于changeIndex
while (leftIndex < size) {
if (leftIndex + 1 < size && data[leftIndex].compareTo(data[leftIndex + 1]) < 0) {
changIndex = leftIndex + 1;
}
if (data[curIndex].compareTo(data[changIndex]) < 0) {
swap(curIndex, changIndex);
curIndex = changIndex;
leftIndex = 2 * curIndex + 1;
changIndex = leftIndex;
} else {
break;
}
}
}
7.测试,直接将数组转换为堆排序
public static void test2() {
Integer[] arr = {62, 41, 30, 28, 16, 22, 17, 29, 19, 15, 67};
MaxHeap<Integer> heap = new MaxHeap<>(arr);
heap.heapify();
System.out.println(heap.toString());
}
public static void main(String[] args) {
//test1();
test2();
}

8.重写toString
//重写
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < size; i++) {
sb.append(data[i]);
if (i!=size-1){
sb.append(",");
}
}
return sb.toString();
}
优先队列
(1)优先队列描述
- 什么是优先队列
- 普通队列:
- 先进先出
- 食堂打饭,先来先吃
- 优先队列:
- 出队顺序和入队顺序无关,和优先级有关。当访问元素时,优先级最高的会被删除。
- 可以使用最大堆这种数据结构作为优先队列的底层结构。
- 医院看病,病情严重者,急诊优先
- 普通队列:
(2)优先队列实现
1.创建优先队列
- 实现之前写的队列接口
- 继承 Comparable需要比较
public class PriorityQueue<T extends Comparable<T>> implements QueueInterface<T> {
}
2.初始化优先队列
- 底层使用最大堆
- 初始化优先队列
- 获取优先队列元素
- 判断队列是否为空
private MaxHeap<T> maxHeap;
public PriorityQueue() {
maxHeap = new MaxHeap<>();
}
@Override
public int getSize() {
return maxHeap.getSize();
}
@Override
public boolean isEmpty() {
return maxHeap.isEmpty();
}
3.入队出队查看队首
- 入队,同最大堆一样
- 出队,优先队列,出的是优先级最高的元素,即最大堆中的移除根节点元素
- 查看队首元素,
@Override
public void enqueue(T ele) {
maxHeap.add(ele);
}
@Override
public T dequee() {
return maxHeap.removePriorityEle();
}
//查看出队(队首)元素是什么
@Override
public T getFront() {
return maxHeap.getMaxPriorityEle();
}
@Override
public String toString() {
return maxHeap.toString();
}
3.测试
public static void main(String[] args) {
priorityTest();
}
public static void priorityTest(){
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
int num = 10;
Random random = new Random();
for (int i = 0; i < num; i++) {
priorityQueue.enqueue(random.nextInt(100));
System.out.println(priorityQueue);
}
while (!priorityQueue.isEmpty()){
int popEle = priorityQueue.dequee();
System.out.println(popEle+"->");
System.out.println(priorityQueue);
}
}
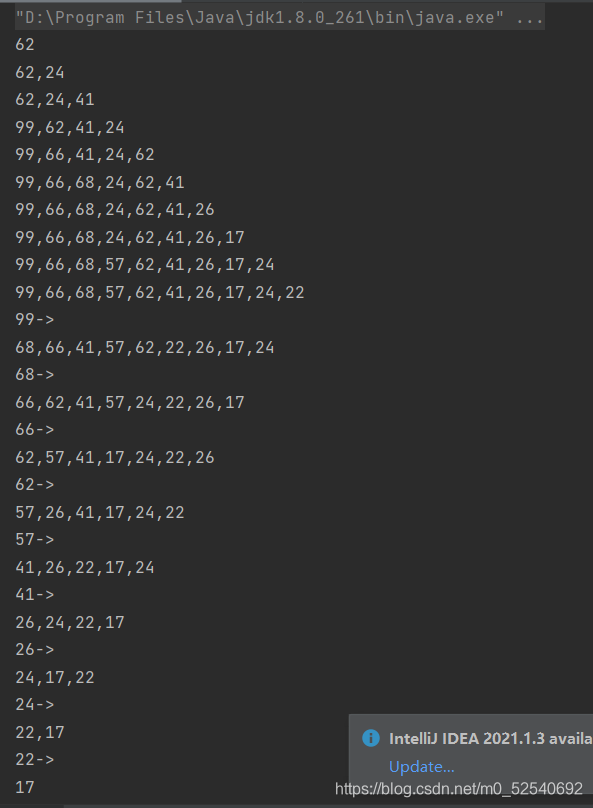
结果如下:
























 4211
4211

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








