数据库课程记录

课程主要内容

这部分都是概念性东西。

CH01

概念模型

考试必考，很多例子多琢磨。

一些概念

E-R方法（重点）

是概念模型的表示方法

-------------------------------------------------------------------------图1----------------------------------------------------------------------
下划线标明的是码–>码是关键的属性
E-R图画法：

1. 用矩形表示实体集，在框内写上实体名。
2. 用椭圆表示实体的属性，组成码的属性加下划线。用无向边把实体与其属性连接起来。
3. 用菱形表示实体间的联系。
4. 将参与联系的实体用线段连接（即上图中的学生连上选修，课程连上选修），线段旁标注联系的类型（即上图的m、n）。
5. 联系也可以有自己的属性。[实体集独自具有的就放在自己那，若需要两个及以上的实体集参与，则放在“联系”处]

几种关系

• 两个以上实体型的多对多联系
  
• 两个以上实体型的一对多联系
  
• 一对多
  
• 联系可以有属性也可没属性
  
  -------------------------------------------------------------------------图2----------------------------------------------------------------------
  成绩这个属性挂在“选修”这最合适。

E-R图→数据库的实现

将图1转化为：

几个实体就要几张表，几个联系就也要几张表。
注：联系的属性这里，用到了这个多对多联系的实体的主码。
（牢牢掌握这个规律）

E-R图设计举例

1. 图书管理
   
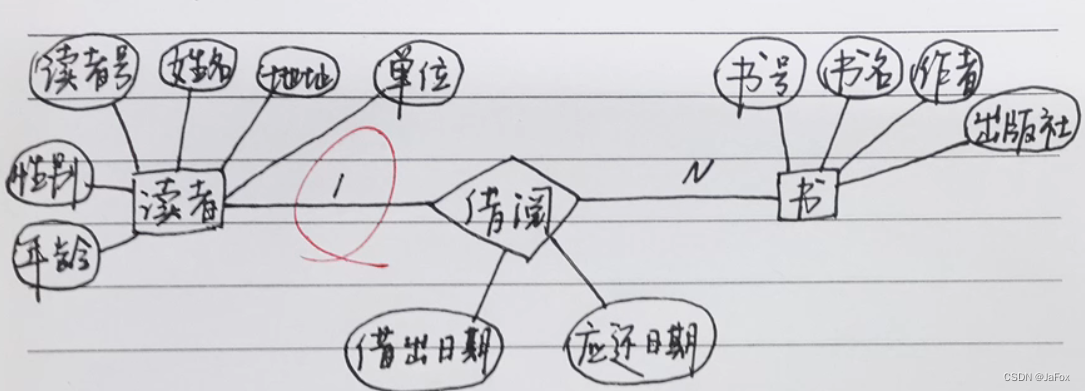
   红笔处错误，应该是多对多：一本书可能被多个同学借过， 一个读者可能借过多本书
2. 冗余
   
   冗余：某个属性的一个值会出现多次👉单独规划出一张表。
   修改方法：将产生冗余的属性用实体表达，如下图。
   
   
   注：一对多的联系不需要单独的一张表，只需要在多端（这里的“酒”）加一个属性。（对比图2，图2是多对多关系，所以联系也转化成了一张表）
   准确的说，是在多端加上1端的主码，作为一列
3. 属性的摆放
   
   上图设计不合理：评分不是食物的固有属性，评分价格也可能和餐馆有关（如不同的餐馆同样的食物，价格不一样）。
   修改为：
   
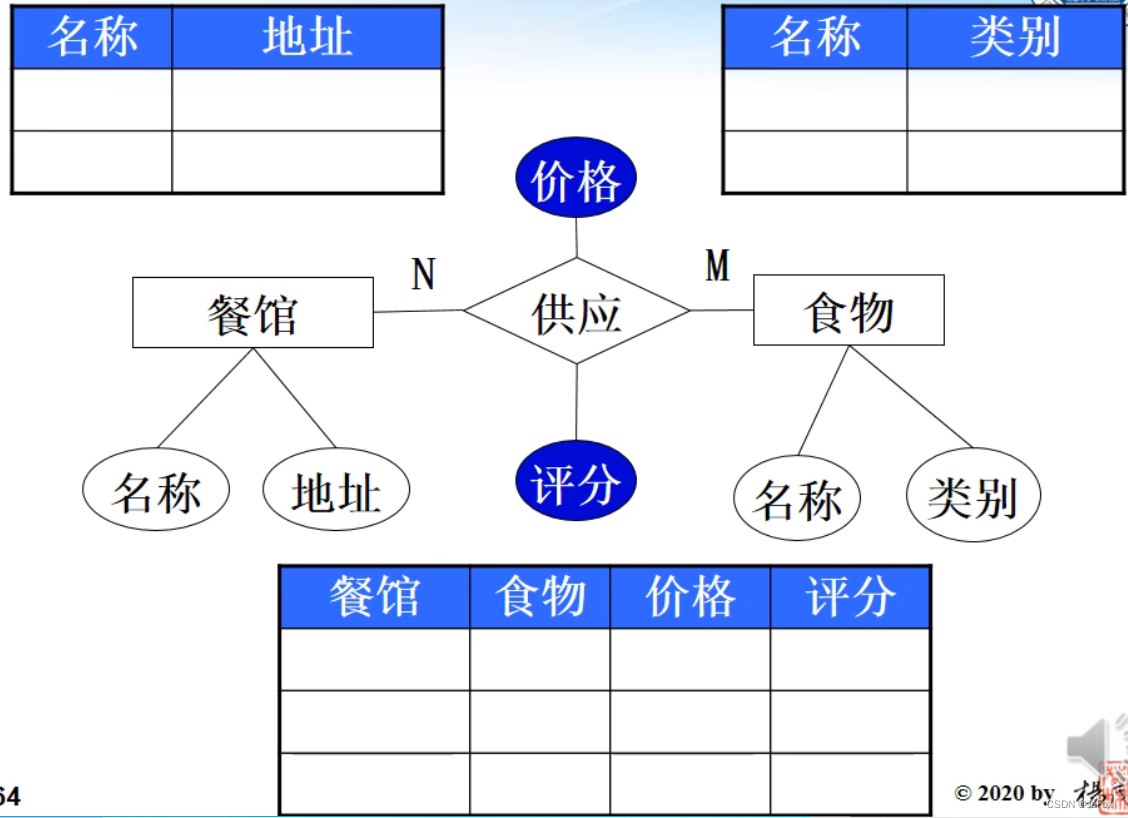
   4. 多对多的转化
   
   现在只能知道一个演员的片酬，但无法知道这个片酬由那几家公司分摊。这就要在“原来的关系上”引入“制片公司”实体，见下图：
   
   当，一个实体集和另一个实体集有关系时，就会有一个什么什么(如指导老师、片酬)，这个就是关系的属性。

层次模型

快速浏览下

网状模型

快速浏览下

关系模型

是我们这么课主要讲的东西

基本概念

注，课程中谈到的所谓“关系”“表”“集合”就是同一种东西。

CH02 关系数据库

笛卡尔积

上图主要看计数的计算方法

关系

例子如：

• 候选码：属性组；全码：很极端的情况下
  
  说明：主码(属性组)是从多个可以唯一标识…的 属性组中 挑出来的一组。
  
  

外码：在关系R的属性组F里面它可能不是(即意味着可以是也可以不是)主码，但在另一个关系S中是主码。
（没有主码就没有外码）
外码的例子：

黄色的“系别”–>是由一对多的转换规则而加上的。
（一对多的转换规则？？）

关系模式

关系涉及到“值”的概念，关系模式涉及到“型”。

域的集合可能≤属性的个数（不同属性可能映射到同一个域）。

通过上下文判断。。

关系数据库

也有“型”“值”的概念。

“型”“值”举例：

参照完整性

意思是：外码的值要么 =空 要么 =主码值 （外码对应的主码）。
例子：

注意）A是可以的，只需关注外码 =空 或 =对应的主码 就行，别想“零件不可能没有来自的厂家”。

关系代数

R∪S并运算：
要求R，S同构的，相同的表结构。

R-S差运算：
也要求同构；S中可以有R中没有的一组元素。

R∩S交运算：
要求同构

连接/串接：

笛卡尔积：

结果的列数=R和S的列数相加，行数=R和S的行数相乘。

象集：
例子①：属性A取常量a1的元组中，BC上的分量，为a1的象集BC。

S的：计算机系女生的学号、姓名。
P_cs145=cs145这么课单科的成绩表，由学号成绩组成。

表中的一行，称为“元组”

中间的表达式 就是选择的条件。

可以用列的序号表示列的名字，从左到右，从1开始。

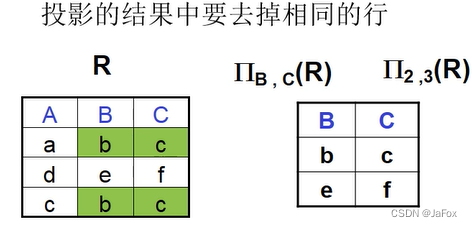
投影的含义是：只要哪几列（去掉相同的行）。
一般，投影和选择运算，不可交换顺序。


选择和投影 都是单目运算。

连接（θ）：就是按照那个条件，逐个挑出合适的。
θ运算总是可以=笛卡尔积，再做一次选择运算。

注意，同名列的处理。

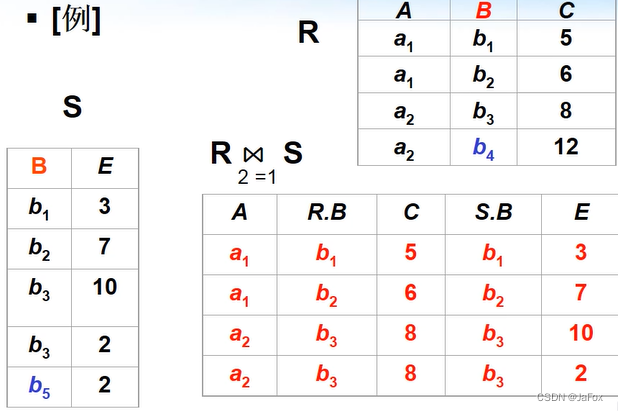
等值连接，且有同名列，做出的结果再合并，得到的是自然连接↓：

悬浮元组：在自然连接中被丢弃的元组，如b₄和b₅在的元组。


内连接、全外连接满足交换律；左、右外连接不满足交换律。

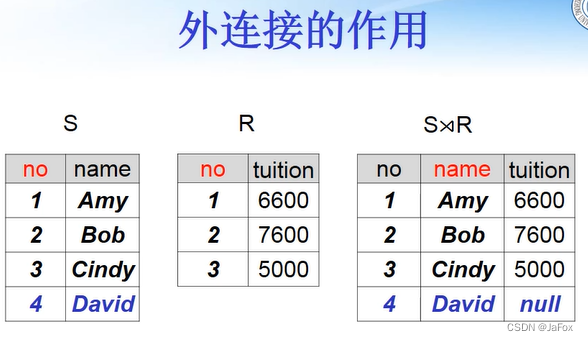
–>希望没交学费的同学也在表上。
自然连接的稍复杂的例子：

↑：悬浮元组被丢弃。

连接，用投影和选择运算表达。
为给除法做铺垫：

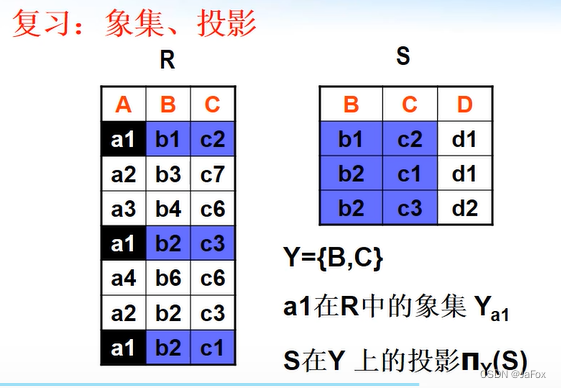
除运算：

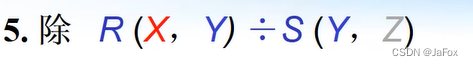
能除运算的前提：R和S有共同的属性组。
Z属性组对除运算没影响，可以直接无视其的存在。

除运算的结果一定来自 共同属性以外的属性（此：一定是一元组，一定是满足条件的A的分量组成==>“条件”：分量在R上的象集 包含S在共同属性组上的投影[这个投影是确定的]）
此：只a1满足。

观察共同属性–>结果一定来自A、B。
除运算的语义：

–>选修了所有课程的学生➗课程。

除运算–>用其他运算表达：

---

一些记号在CH02-Part2 43：49左右

---

CH06

问题的引出：否则改数据得一次性改很多。

函数依赖

概念函数依赖

判断函数依赖，找X属性上值相同的两个元组，对应的Y属性上的元组间的值是否相同。
排除函数依赖，根据定义中的“任意性”，找一组反例就行👇


👆整体U满足，子集V肯定也满足。

注意一下👇

平凡函数依赖、非平凡函数依赖

定义：→的两边，“右边是左边的子集”是否成立。
so,平凡函数依赖总是成立的，一般不去讨论。

完全函数依赖、部分函数依赖

完全：X属性组里的所有属性必须都在，才能决定Y。
部分：存在一个，X属性组里的部分属性，就能决定Y。

传递函数依赖

定义：X→Y，Y→Z，则X→Z。
注意：
(1) 前两个不能是 平凡依赖(即子集的那个)。
(2) 若X<->Y，则Z直接依赖于X（也Y）。

码

👆属性全集U，完全依赖于K。
候选码：是一组属性，能决定其他所有属性，它的闭包=U。(且这组属性去掉任意一个属性，其闭包≠U)
码：主码和候选码的统称。
包含在任何一个码中属性，叫主属性。
（极端情况下）全部属性集U为码，称为全码。

函数依赖的公理系统

范式判定，模式分解算法的基础。

逻辑蕴含、闭包

• 蕴含：不论X→Y(念成X决定Y)是否显示地列在函数依赖集F中👇
  
  so，可以定义成：（F推导出来的函数依赖）
  - 闭包： F所蕴含的函数依赖（F推导出来的函数依赖）的全体，称F的闭包(F⁺)。
  
  注意，属性集的闭包👇。
  X⁺_F 的意思：F推导出来的，X决定的属性，这些属性的集合。
  
  找闭包(函数依赖集的、属性集的)，不能只看F中显示地列出的，需要运用规则去找新的。

Armstrong公理系统

由三条规则组成。通俗的说：
(1) 自己决定自己及自己的子集。[这是平凡函数依赖，和F没关系]
(2) 在函数依赖两边加相同的属性，仍然成立。
(3) 传递。
正确性： 从F出发，根据三条规则推导的一定成立，且在F⁺中。
完备性： 在F⁺中的也一定能👆这么推导出来。

为了更简洁证明，推导出很有用的规则：
(1) →左边相同，右边可以“乘”起来。
(2) →右边可以变成“右边‘乘’右边的子集”。[就是(1)的变形， 加个找右边的字节]。也即，X决定Y的任何一个子集。
(3) →左边的可以替换右边的。

几个定理和求闭包的算法及其应用

引理6.1

由上面的内容，很容易得出结论：（等价符，念成当且仅当）

引理6.2

问题：

F⁺求出来意义不大，又经常要判断某个依赖是否成立。

(👆看最后的式子就行。这式子也是显然呀。。。)

引理6.3

(👆由前面的引理，也容易得出)

求属性的闭包

(程序性的方法)

Armstrong推导也是方法（来证明某个函数依赖成立），但太麻烦。

（👆看例子就行）
(1) 初始化属性集闭包为自己。
(2) 扫描F中的每一个依赖。若该依赖的左边(左边的所有属性)在已有的属性集闭包中，就把右边并入属性集闭包。
(3) 若闭包＝U(整个属性集)了，就提前退出。
(4) 一个循环，扫描一遍F。若一次F扫描完了，属性集闭包变化了(相对扫描这遍F前，有新元素增加)，就再扫描一遍F。

例子：（很简单）


属性集闭包是第六章最重要的工具：可以用来①判断函数依赖的成立👆②求主码👇[在下一节的应用中也有]

第一题：给定的是关系模式的 属性集 和函数依赖集F。

主码只有自己决定自己，不能被其他属性决定。所以：
(1) 一个属性没在非平凡的右边出现过，那么它包含在主码中[≠是主码]。
(2) 若这个属性👆的闭包＝U，则这个属性是主码。若闭包≠U，需要补充属性(在→左右两侧挑选， 逐一试探)。
如题：
【例题1】

思路：CE没在右边出现过，求出它们的闭包，发现=U。
【例题2】

思路：先发现CE不在右边出现，其闭包≠U，故需要添加元素
先考虑单属性再双属性等实在不行就 全码。
（注意：考虑单属性就要考虑所有可再加入的单属性，但找到＝U之后就不要再找双属性了，因为肯定是多余的。）
【例题3】


方法1，求闭包挺简单。

函数依赖集的等价和覆盖

引理6.4

极小函数依赖集

最小依赖集，最小覆盖

👆(3) F的所有函数依赖的左侧没有冗余属性（即去掉这个属性后的函数依赖集不能和原来的等价）。
求最小依赖集：
（方便记忆，处理的部分：右边，整个，左边）
[先初始化F_m=F]
(1) 右边单属性化
(2) 去掉多余的函数依赖：逐个考察每个依赖，F减它得G，在G下证明这个考察的依赖是否成立（用求闭包证依赖的方法）。
(3) 去掉函数依赖左边多余的属性


F的F_m不唯一，且两等价的F_m（同一个F的F_m）中的依赖的个数都不想等👇。

【例题】：


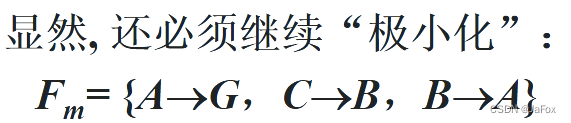
(别想G1、G2的作用)
思路：考虑能C或G多余，即可以用G或C取代CG。若C多余，就求G关于F的闭包，看是否含有B(含有就说明G能替代CG)；若G多余，就求G关于F的闭包，看是否含有B。

应用：求关系模式R<U,F>的候选码

👆定义知道就行（非教科书上的）。
结论1：不在任何依赖的右边出现的属性，必出现在每个候选码中（一定是主属性）。
结论2：仅在函数依的右边出现的属性一定不是主属性（不会出现在任何候选码中）。

👆（1）只要尽快去除冗余就行，不是非要做到最小覆盖。

范式和规范化

https://blog.youkuaiyun.com/legendaryhaha/article/details/80032808

概念

1NF

1范式：其实就是说 列不可分。

2NF

若R∈1NF，且每一个非主属性完全函数依赖于码。

推论正确（别管“为什么”）。

3NF

其实说的就是消除 传递依赖。每一个非主属性都要直接依赖于码，不能传递依赖于码。👇

注意，是非主属性的传递。

👆更严格的说就是不能出现“不允许”中的模式，注意XYZ的身份。【Y决定Z不能是平凡的函数依赖】

👆因为只有两个属性，不存在传递的第三个属性。

👆为联系：BCNF一定是3NF。


👆步骤：
（1）根据题目翻译出F
（2）求这个关系的候选码[之前讲的那些]
Answer：
不能忽略，J是主属性，因为有两个候选码，没有非主属性，所以就没有非主属性传递或部分依赖于候选码。
没有非主属性的关系凡事一定是3NF。

---

前面的三个范式是针对非主属性的，BC范式则是针对于码。

BCNF

BC范式最容易辨别：它的每一个非平凡依赖的左边一定包含候选码。

BCNF是函数依赖范围内能达到的最高范式。

多值依赖

区别于函数依赖的另一种数据依赖关系。

定义：

例子👆，参考书多值依赖于课程。

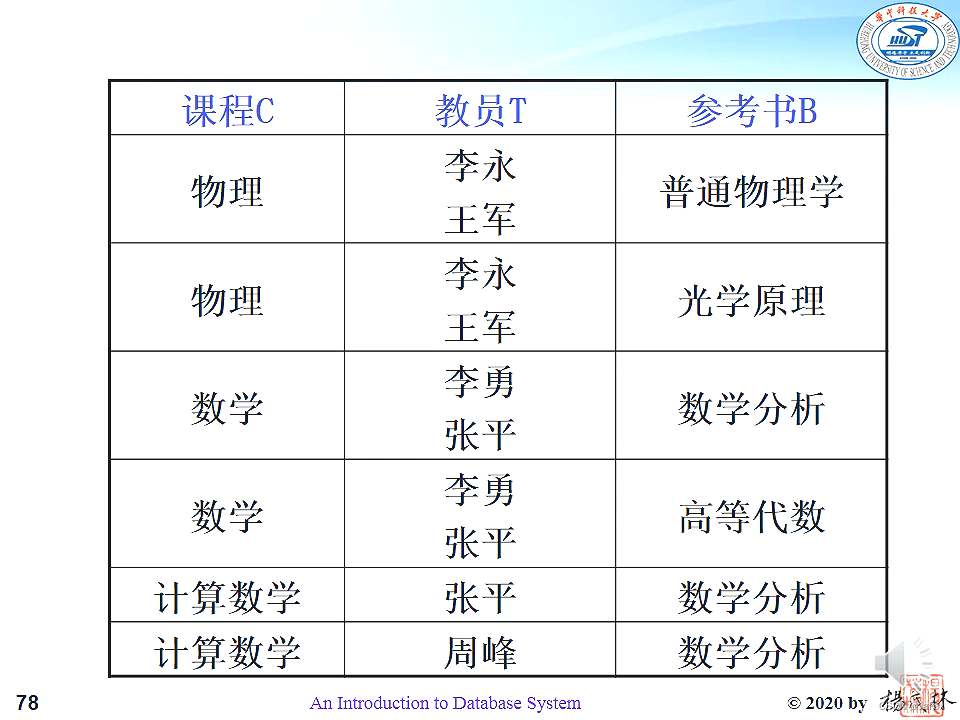
👆教员多值依赖于课程。

4NF

规范化小结

要牢牢掌握各范式的判定要点

关系模式的分解

定义

求函数依赖集的投影

模式分解中的问题

无损连接分解

保持函数依赖的分解

关系模式的分解算法

CH09

代数优化

归纳下 等价变化规则（关系代数表达式的）：

通常，“交换”都是有前提条件的。👆

穿过一个自然连接时，自然连接的属性是是cnumber，所以目标属性自动加上一个cnumber。总之，投影运算在下移的过程中要保留连接的属性

第5步不是重点掌握。

物理优化

小结

CH10

一致性状态：不含只做一半的事务。

这两条语句都做，都不做才处于一致性状态。











仍表现为前三种。

只能恢复到转储时的状态。
恢复到故障发生时的状态，先恢复到转储时，再运行到故障时。

👆挺重要，可以处理……故障，……故障，协助副本进行……故障恢复。








尚未完成的事务：在日志文件中只有开始标志没有结束标志的事务。














建立一个检查点，意味着把之前所有的日志和数据库的修改写入磁盘。


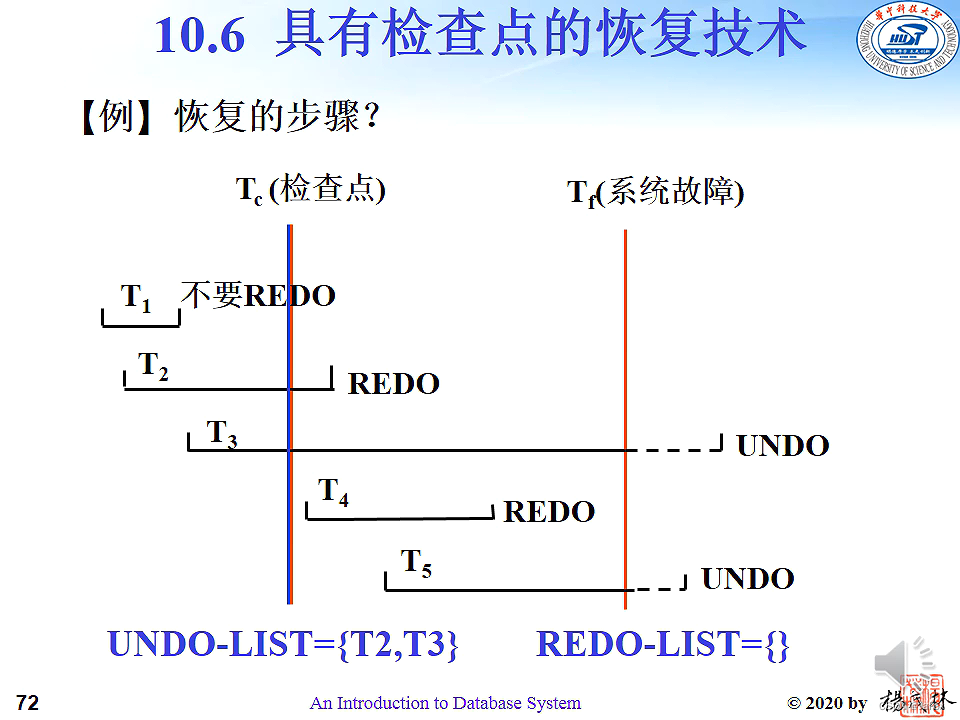
检查点建立时的active-list。

操作：就是从检查点开始，扫描到开始，加入到UNDO-LIST，扫描到结尾，加入REDO-LIST。初始化：检查点时正在执行的事务–>都先成为UNDO-LIST。
一直扫描到日志文件结束，如到系统故障处。

CH11

这么多可能性，可能有会出错的结果。

串行调度一定正确。




机场买最后一张票的例子。