Diffusion Model 原理剖析

Diffusion Model 原理剖析

原理剖析1

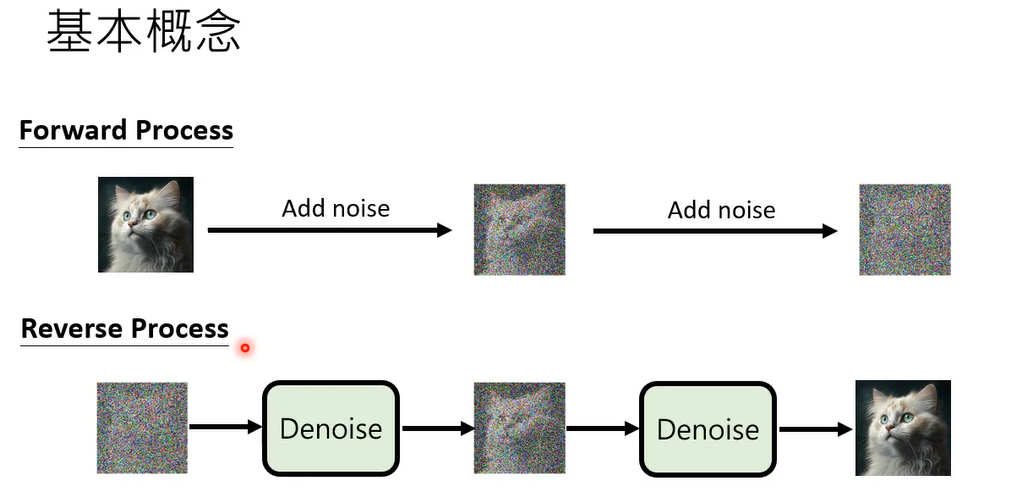
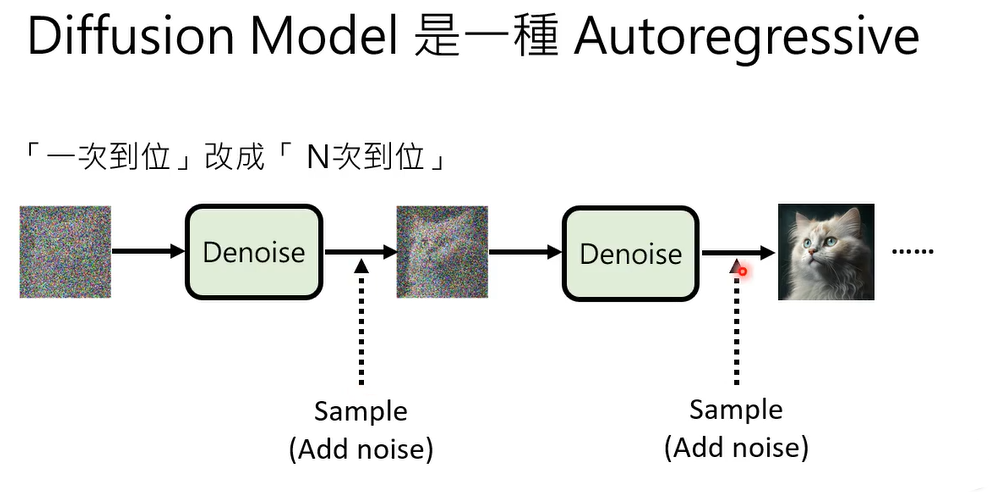
好那diffusion model的概念,那我们两周前讲过了浅谈图像生成模型 Diffusion Model 原理,其实非常的直观,而且有一个forward process,把这个forward pases就是把noise加到image里面去
,直到你看不出来原来的图长什么样子,那有一个reverse process,这个reverse process呢就是做denoise,你先给他一个全部都是noise的image,那每次denoise的过程中,这个图像都会浮现一点点出来,直到最后完整的图像被产生出来,所以diffusion的概念就是这个样子

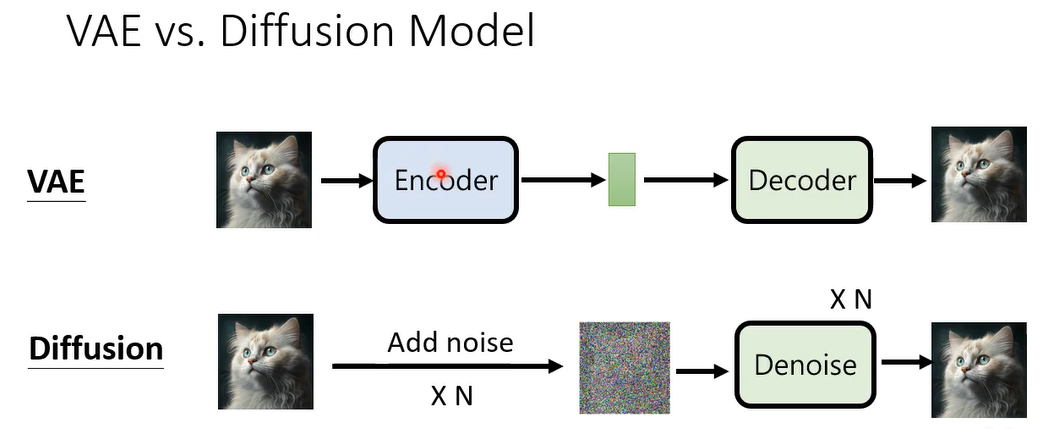
Diffusion model 和VAE非常的像，vae一就是先有一个encoder，把image呢变成latent representation，然后再一个decoder，把这个latent representation还原回image。那diffusion model呢它就你可以想成加noise的过程，其实就是在做encoder，只是这个encoder不是一个neural network，不是learn出来的，这个noise加进去的process是已经固定好的，他不需要学习，是人设计的，那你透过加noise的过程加n次noise，把一张image变成一个只有杂讯的东西，完全看不出来它是什么，那这个只有杂讯的image，就相当于v a e里面的latent representation，然后dnoise的过程就相当于vae里面的decoder，把都是杂讯的图，还原成原来的图啊，这个是diffusion model跟v a e他们的关联

那上周的留了一个伏笔告诉你说，其实diffusion model的演算法非常的简单，在DDPM这篇paper的原始论文里面呢，其实就是这样，两张图就是diffusion model演算法的全部，但是两周前留了一个伏笔，说这个演算法里面呢其实暗藏玄机，如果你仔细读一下这个演算法，你会发现，似乎跟我们两周前讲的概念，有一些不一样的地方，那我们就先来看看这个演算法里面在做什么好，先来看训练的演算法啊

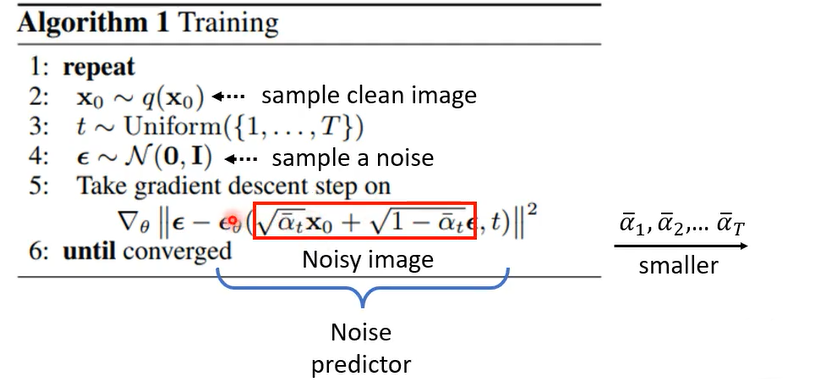
在训练的演算法里面要做的事情是什么呢，而这个第一行是repeat，就以你一直做第二行到第五行的这些事情，直到converge位置好，那这个呃第二行做的事情是什么呢，第二行做的事情是说我们先要simple一张image，叫做$x_0$，在diffusion model的这个文件上啊，通常把x0 当做是干净的图，就是你要呃就是真正的图也要生成的图哦，所以x0 代表的是干净的图，也就是你从你收集到的影像的资料库里面，抽一张图出来啊，就是x0就是第二行做的事情，而第三行呢是simple的t哦，从一到大t这个数字间simple一个整数出来，那这个大t套会设一个比较大的数字，比如说1000哦，所以从1~1000里面simple一个数值出来，比如说968啊，然后这个然后接下来呢你会有个ε，这个ε呢是从一个normal distribution里面simple出来的，那这个normal distribution呢它的mean是0，那他的这个variance，每一个dimension variance呢都固定是1啊，就从这个normal distribution里面simple出一个ε出来，那这个ε它的这个大小呢会跟image是一样大的，不过它里面全部都是杂讯，所以你看不到任何有意义的图

那接下来呢第五行是比较复杂的，我们先来看第五行，红色框框里面做的事情，红色框框里面做的事情是把x0跟ε做Weighted average,，weight 是什么呢，这个weight呢是事先定好的哦，从阿尔法1到阿尔法t吧，我们事先定好了一组位，从阿尔法1一直到阿尔法T，那你把x0 和ε做Weighted sum，你得到的就是一个有杂讯的图。x0 跟ε用某种比例混合起来以后呢得到的就是一张有杂讯的图.

阿尔法1到阿尔法t的设计通常是由大到小，所以所以今天如果你simple到了这个t越大的话，那就代表阿尔法越小，那阿尔法越小意味着什么，意味着原来的图x0 占的比例越少，那你的noise 呢占的比例越多哦，所以这个t simple到的越大，代表说我们noise加的越凶狠，加的越多，那我们就得到了一张noise的image，接下来做的事情是什么呢，这边有一个看起有点复杂的式子

${ϵ}_{\theta }$是一个函数，这个function的输入是Noise image和t，这个函数就是Noise predictor，这个noise predict ，the network呢就是吃一张noisy的image
吃一个simple到的数值t，然后呢他就产生一个noise

那我们现在学习的目标是什么呢，他的意思就是说我们这个noise predictor，他要output的目标是什么，他的ground truth是什么，它的正确答案是什么，正确答案就是你当初sample出来的那个noise，你当初sample出来，跟clean image混在一起的那个noise 了。画个图可能更加清楚，我们先准备好一排数值阿尔法，阿尔法1到阿尔法T啊，然后呢从你的资料库里面抽一张图x0 出来

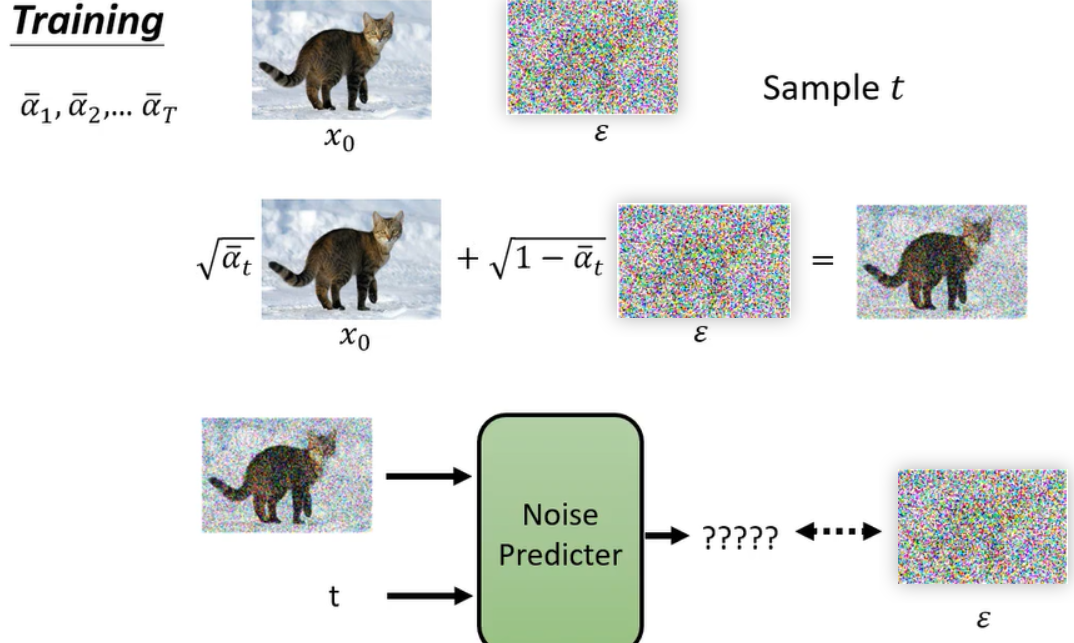
那我们就是simple一个noise出来，然后呢simple一个整数提出来。然后我们就把我们simple到的干净的图成一个比例，加上噪音乘一个比例，而得到一个杂噪音的图。接下来呢你要训练noise predictor，他就是吃这个有噪音的图，混入噪音的图加上呢呃一个数值，一个整数，然后呢他要输出呢呃去预测呢，混入的噪音长什么样子啊，他要去预测混入的噪音长什么样，好在这个是实际上d d p m diffusion model，它的演算法真正做的事情

如果你在回忆起我们上次上课讲的东西，你会发现其实是有点不太一样啊，上次讲的是一个概念中的讲法

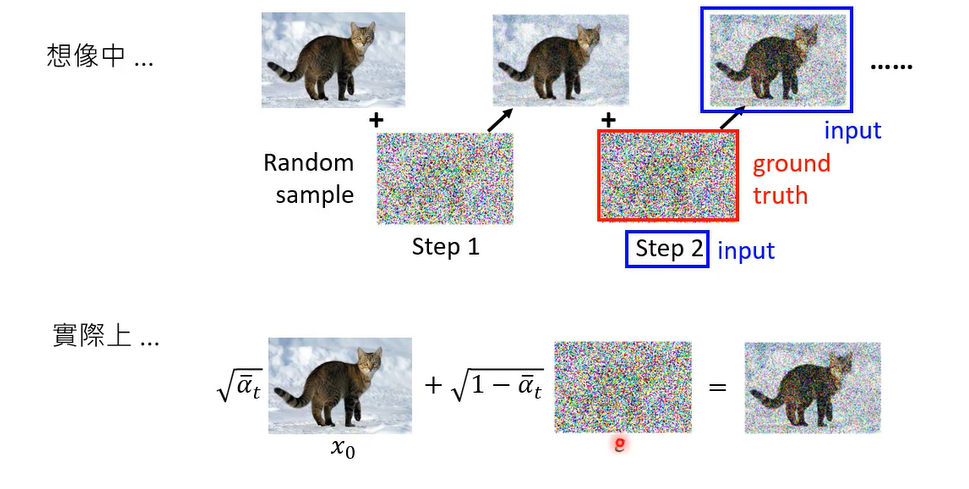
就是在我们的想象中呃，这个diffusion model的运作应该是这样子的，每次你有你有个最干净的image，加点噪音变得有点杂，再加多一点噪音变得有一点杂，然后你每一次训练你的noise predictor的时候，他是把有杂讯的image当做输入，然后呢再给它一个数值，然后他预测的是混入的这个杂讯，但是它还原的结果是要还把有杂讯的图还原成，有一点没有那么杂讯的图，但是它还是有杂讯的。

但是实际上实际上dd pm的演算法，做的事情是干净的图，直接混入一个噪音，那这个噪音呢透过$\overline{{\alpha }_t}$决定那个噪音的大小

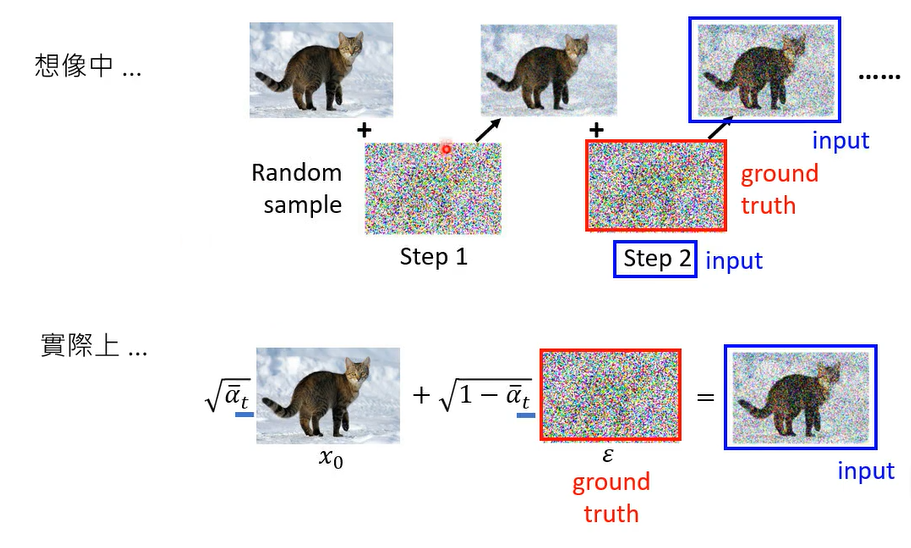
然后呢训练的时候呢，就是把有噪音的图跟t当做输入，直接预测混入的造诣，那你发现说实际上做的事情，跟我们想象中做的事情其实是有点不一样

在我们想象中，杂讯是一点一点加进去的，dnoise的时候也是把杂讯一点一点的抹去，但是实际上我们真正做的事情，杂讯并没有一步一步的加进去，并没有加多次杂讯，一次就把杂讯$ϵ$直接加进去，然后呢在denoise的时候，也是一次就要把$ϵ$ denoise出来

为什么是这个样子，那等一下的数学推导非常的差，那等一下东西，如果你听不懂的话也无所谓，你就印记说哎d d p m其实就是这样子的，跟你想象的有一点不一样啊

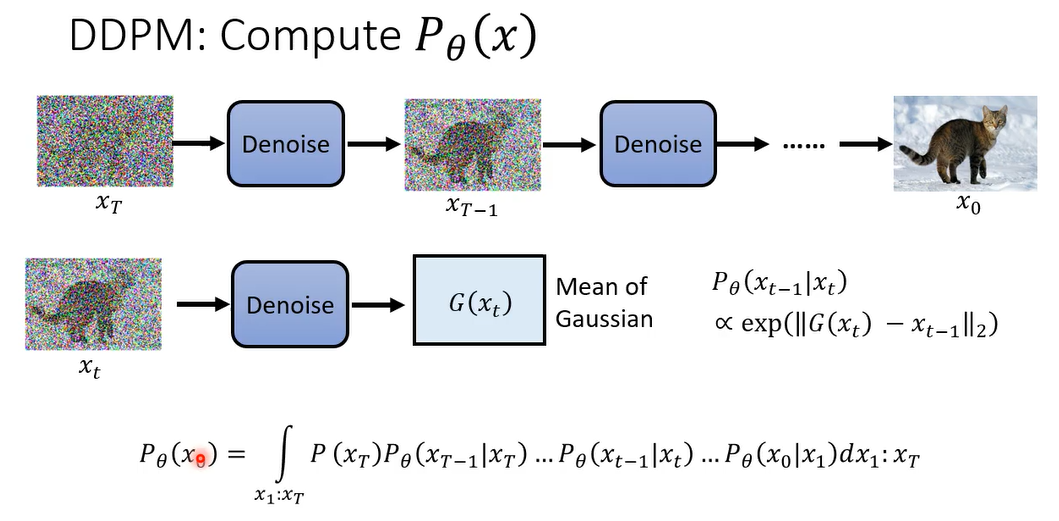
好那我们再来看看产生图的过程，产生图的过程是这个样子的，我们一开始呢先这个simple一个全部都是noise的图，这个叫做$X_T$，那在diffusion model的这个文件里面，通常把$X_T$代表一个纯粹都是杂讯的图，我们simple一个纯粹都是杂讯的图啊，接下来就开始做，接下来呢就开始跑这个reverse process，开始把图产生出来,那他总共要跑T次，所以这个t等于T到1

当你发现每次生图的时候，首先它都要先升一个noise出来，这边又再simple了一次noise，就这边已经sample过一次noise，得到x大t了，这边不知道为什么居然要再simple一次，得到z

下面这个式子做的事情是什么呢，这个式子做的事情是这样子，我们有xt啊，我们x t这个是在上一个步骤中，已经产生出来的图，那一开始t等于大t的时候，那这个xt就是一个纯粹的杂志，不过这边是iterative不断的循环的跑的，xt是上个步骤产生出来的图

好把x t减掉，这边有个${ϵ}_{\theta }$（$x_t$, t）这个是什么，这个是dnoise的那个那个noise predictor啊，output出来的noise，乘上一减阿尔法t除以根号一减阿尔法t拔，然后乘上一除以根号阿尔法t，然后呢还要再加一个noise，这个noise前面有乘一个常数，叫做${\sigma }_t$，然后得denoise的结果叫$x_{t-1}$

那如果这个式子你看的有点模糊的话，以下就用图的方式来呈现它好，上一个iteration产生出来的图叫x t好，然后呢你要准备好两组那个呃数值的序列，阿尔法1到阿尔法t拔 ，还有阿尔法1到阿尔法t

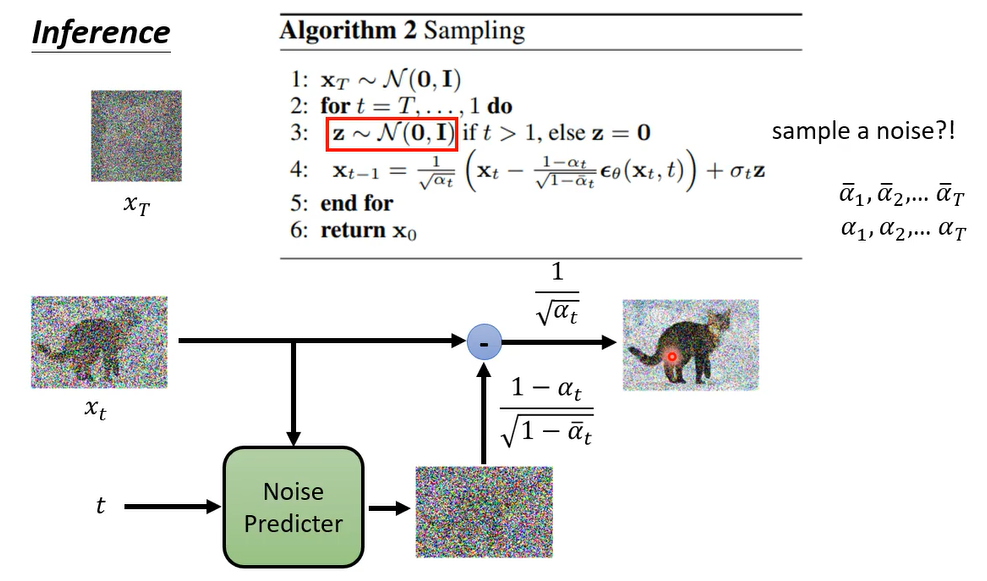
然后呢noise predictor 吃xt这张图当做输入，吃t当做输入产生一张图片，产生一个noise prediction的结果，它predict出一个noise出来，然后呢把这个noise呢减掉x t啊，把这个noise呢减掉x t，然后呢这个noise减之前呢，你要乘上一个呃常数，这个是一减阿尔法t除以根号，一减阿尔法t拔

那相减完之后呢，你要乘上这个一除以根号阿尔法t，但是这居然不是我们最终的结果，本来在我们的想象里面，我们就是把noise predict出来，然后把有杂讯的图解掉，杂讯就应该得到更干净的图，照理说应该就是这个样子就结束了。

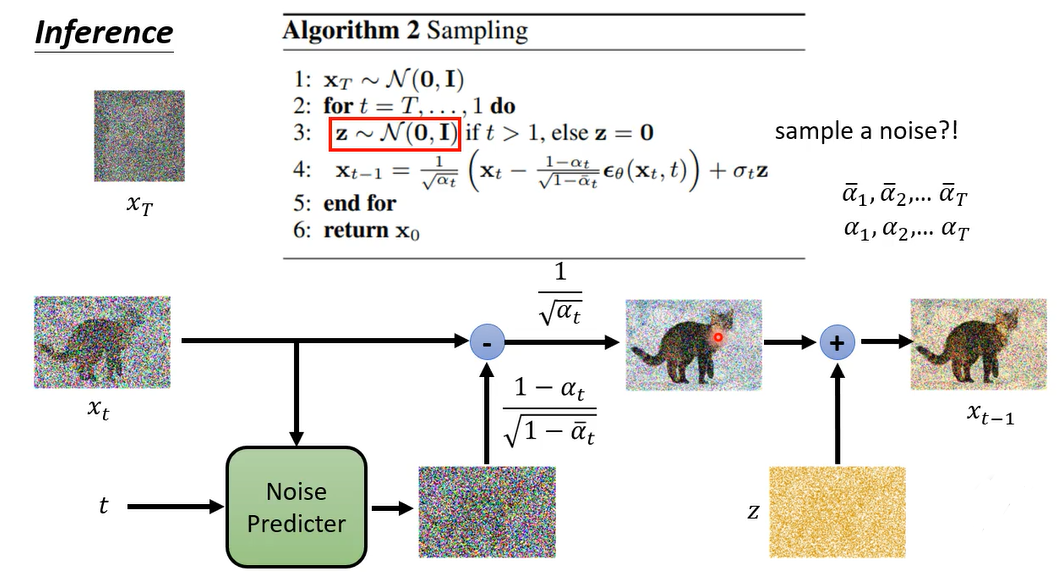
那这里有个奇怪的玄机，不知道为什么还要再simple一个杂讯，把这个杂讯再加到你的影像里面去，得到最终的输出，这个也是一个令人匪夷所思的操作

原理剖析2

这边呢要话说，从头我们要从影像生成模型，本质上共同的目标开始讲起，那影像生成模型本质上共同的目标是什么，它本质上共同的目标是在input的地方，你有一个简单的distribution，你知道怎么做，simple的distribution通常就是一个gaussian的distribution，那可能设成mean是0，然后每一个dimension variance是1。

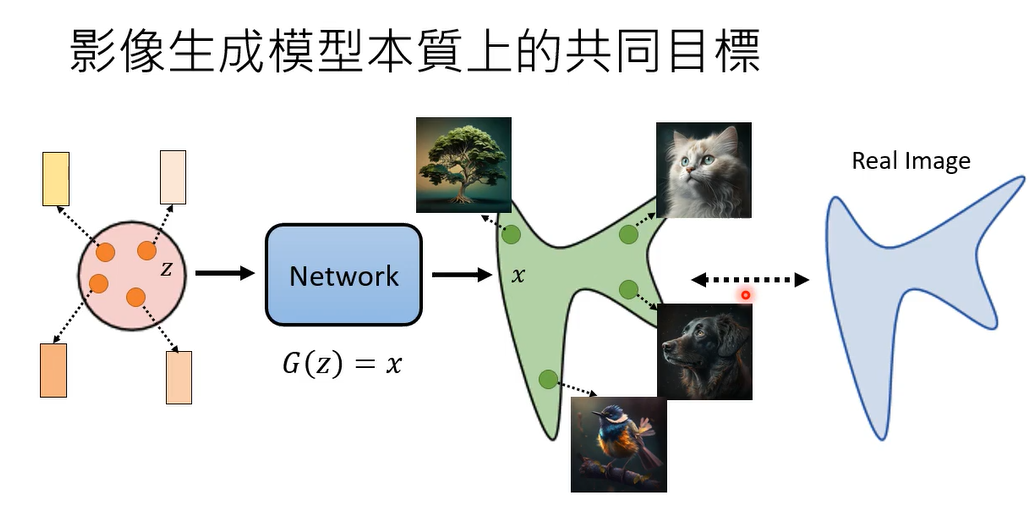
就这样一个简单的distribution，那从里面呢simple出一个东西出来，比如一个vector出来，然后把这个vector呢丢到一个network里面去，这个network我们用g来表示，它的输入是z啊，还有输出是x，那这个x呢就是一张图片，那我们每次呢从input这个简单的distribution sample，一个vector出来，simple一个vector出来，那通过这个network就变成一张图片，simple一个vector出来，to network就变成一张图片，就算是输入是一个非常简单的gaussian的distribution，通过这个network的转换，它输出会变成一堆图片，这些图片会组合成一个非常复杂的distribution，而我们期待的事情是我们找到一个network，这个network应该做到的事情是跟真正的图片的distribution，真正的图片所形成的distribution越接近越好，这个是影像生生成模型，本质上所有各种不同的方法都在奋斗的目标

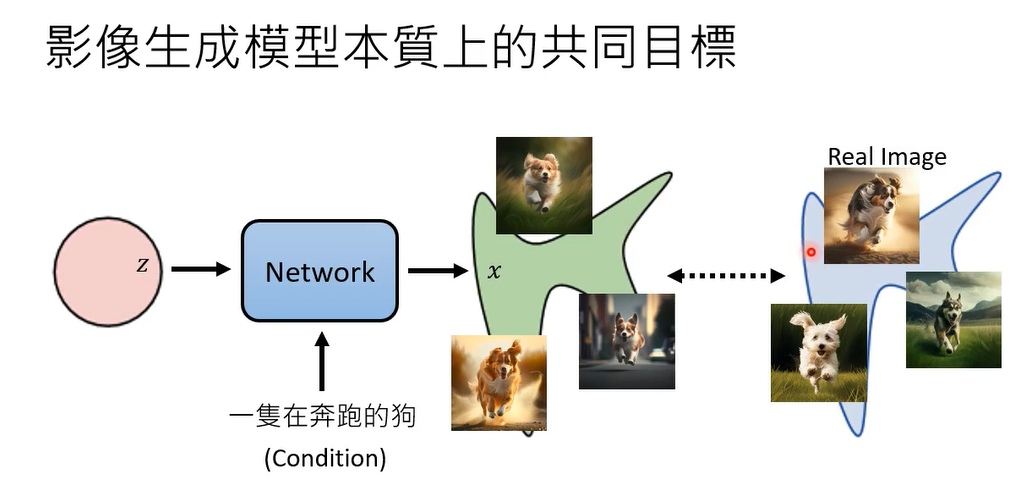
那我知道说今天做影像生成啊，也不是只有生成图而已，通常更常见的应用是直接给一段文字，叫你把图生出来，那但在原理上并跟我们刚才讲的影像生成模型，本质上共同的目标并没有什么不同，多加了一段文字，通过这段文字我们叫做condition，通常多加了condition以后，我们生成出来的是，根据这个condition所产生出来的图片，但是它仍然是一个distribution。

因为我们上次说过说，当你说一只正在奔跑的狗，虽然文字是一直在奔跑的狗，但是影像它可以千变万化，因为一张图片胜过千言万语，只拿一个句子是没办法描述一张图的，所以当你只输入一段文字，要机器生成出图片的时候，他的目标其实是产生一个distribution，产生所有各式各样在奔跑的动，那我们的目标呢一样是要让今天产生出来的distribution，跟真正的distribution越接近越好，所以当影像生成模型，有加上文字的conditions的时候，并没有什么本质上的理论上的差异啊，所以我们等一下再讲接下来的课程的时候，我们都假设没有这个condition，这样等一下的数学是更简洁一点，但是在实际应用的时候，有加上这个文字的condition，并不会影响你的演算法，并不会有太对你的演算法并不会有太多的影响

那我们刚才讲出我们的目标，就是希望这个network，它输入从某一个distribution sample出来的东西，它产生另外一个distribution，而它产生出来的distribution，应该跟我们一个目标的distribution越接近越好，但是什么叫做越接近越好呢，怎么衡量所谓的两个distribution越接近越好，这件事呢

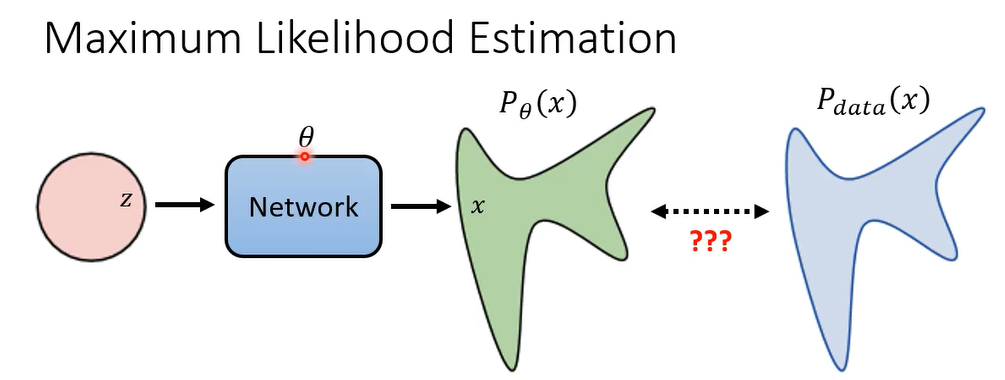
那多数的这个影像生成模型采取的都是呃，maximum likelihood estimation，什么叫maximum likelihood estimation呢，他的操作是这个样子，我们假设network呢它的参数我们用$\theta$来表示,然后呢，这个根据$\theta$这个network产生出来的这个distribution，我们用$P_{\theta }$来表示，真正的distribution我们用$P_{data}$来表示

首先我们从p data里面simple出一堆的image（其实就是你今天在训练模型的时候，你需要一些训练资料，那这些训练资料你要想办法找到，你可在网络上收集的，可能是你买来的，总之你收集到了一堆训练资料，那你收集训练资料，这个过程其实就是从全世界所有可能的图，也就是p data里面取样出一些image出来，取样一些图出来啊）就是x one到x m

那这边呢我们假设我们能够计算$P_{\theta }$，产生某一张图的几率，那这件事情实际上可能是做不到的，因为$P_{\theta }$的非常的复杂，它不是一个gaussian的distribution，它是一个非常非常复杂，你难以想象的distribution，那既然它是一个你难以想象的distribution，随便给你一张图，你可能是算不出这个图，根据这个distribution产生出来的几率的，但是没有关系，我们就是先假这我们可以做到这件事

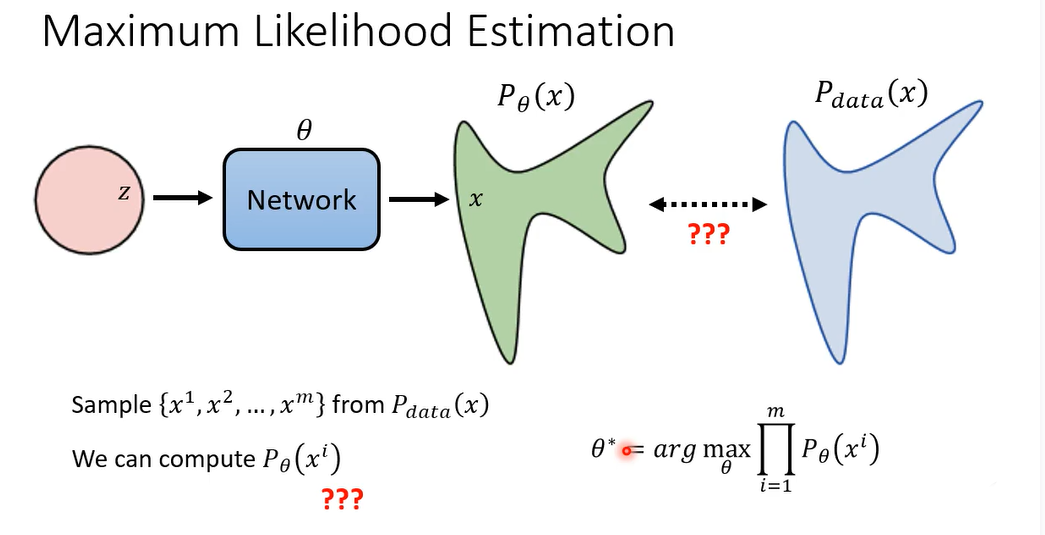
那接下来我们要找什么样的$\theta$呢，我们要找的$\theta$就是可以让我们simple到的这些图产生出来的几率最高的那个$\theta$，那你的objective function，你要去maximize的目标是写成这个样子的，你要去找一组参数，这组参数可以让这个式子的值这最大，这个式子是什么，这个式子就是对你sample到的每一张图，你都拿$P_{\theta }$去算他的产生出来的几率，你把你simple到的图，x one到xm每一张都计算$P_{\theta }$产生它的几率，然后全部乘起来啊，你要找一个$\theta$，让x one到xm产生出来的几率越大越好啊，这个可以让这个x one到x产生出来，几率最大的那个$\theta$，我们叫做${\theta }^{\ast }$，就是我们今天学习的时候要找出来的结果,那其实不同的影像生成模型，他们用的都是这种maximum likelihood estimation.

有人会问说，到底让这些x one到x m产生出来的几率越大越好是什么意思，跟上$P_{\theta }$和p data越接近越好有什么样的关系呢

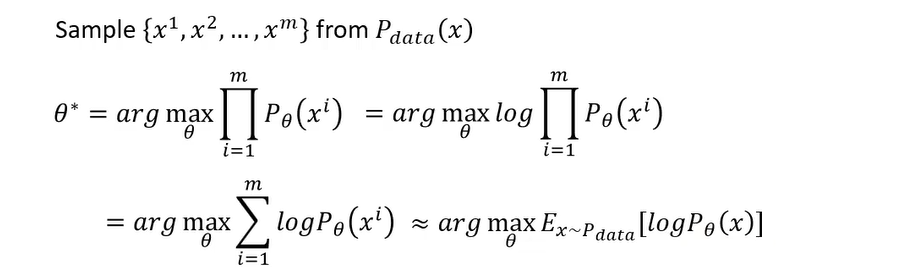
可以对之前的式子取log，不影响结果，log可以把乘传换成加。

我们从p data里面取x出来，然后做$P_{\theta }$计算，log（$P_{\theta }(x)$），然后取x从p data里面simple出来的期望值，那这边呢因为我们一般在我们一般的操作中呢，这个image呢是已经先simple好的，所以我们这边可以取一个sumension，但是这件事情实际上可以近似于，假设你就是不断的从p data，比如说从网络上所有的图里面不断的找图出来，不断的爬图出来，那你要不让你所有爬到的图呢，它的log（$P_{\theta }(x)$）都越大越好

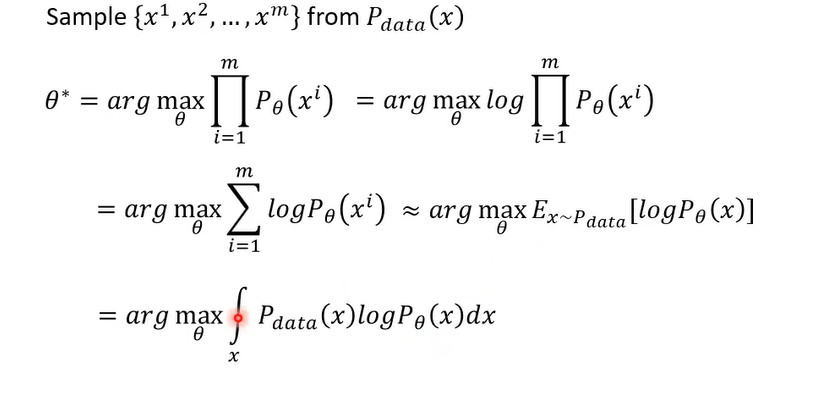
约等于这一步涉及大数定律，后面转成积分则是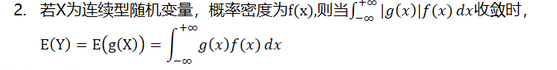

这边呢有一个匪夷所思的操作直接剪掉即对x做积分Pdata x log Pdata x这一项有什么用呢，这一项毫无用处，因为它不会影响你的结果，这一项跟因为我们现在要找的目标是network的参数，那是谁的，那这一项只跟你的data本身有关，只跟这个世界上的image长什么样子有关，跟$\theta$没有半毛钱关系的，所以加入这项完全不会影响你的结果，但加入这一项的好处是什么呢，加入这项好处是，我们现在可以把这两项合并在一起，这两项合并在一起

那对于这些影像的生成模型来说,像va e啊,diffusion model啊,还有flow base model,他们都是试图去maximum likelihood.。那像gan的话，gan是minimize某一个divergence，但它通常不是minimize kl divergence，最原始的gan他是minimize js divergence，如果你想知道的话，反正它就是另外一种divergence

那后来wgan啊是Wasserstein Distance，那你其实也可以修改一下gan的formulation，让它变成mini KL divergence，只是做出来不会更好，就是所以gan要mini KL divergence也是可以的

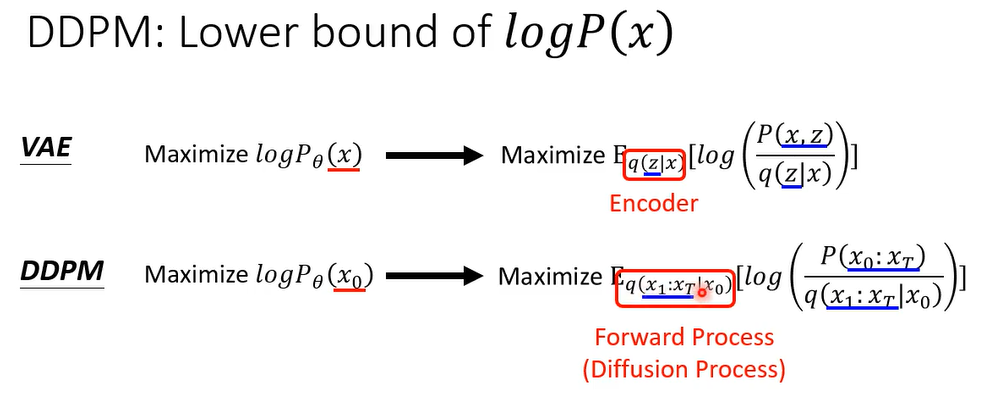
那接下来呢我们先看一下vae，那v a e是过去上课录音里面有的东西，那希望你有看过这段录音VAE，那等一下讲的几页图片，哎其实就是从之前的图片稍微改一下而已，那之所以先讲VAE，一是要让你知道说VAE和diffusion model，他们非常的类似，所以很多v a e里面推导过的东西，对diffusion model来说是不需要再推导一次

那我们先来看一下在VAE里面，所谓的$P_{\theta }(x)$ 它是长什么样子，呃我们说这个$P_{\theta }(x)$ 是什么东西呢，啊就是我们把input的，从高斯distribution sample出来的vector，通过network所形成的distribution

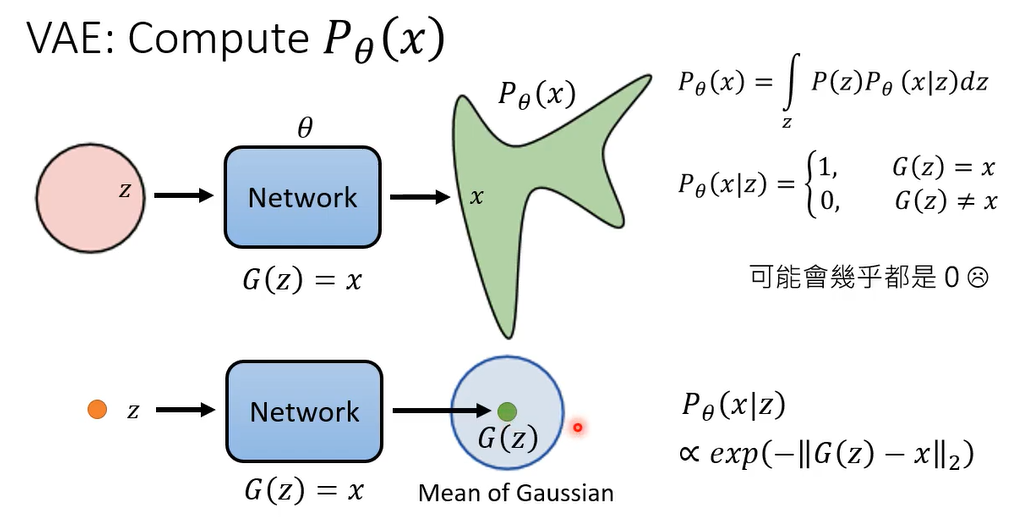
G(z)代表的是mean of Gaussian，这个$P_{\theta }(x|z)$那，他的这个probability density 呢，正比于这个G (z)跟x的距离啊

好那我们通常在算这个v a e的时候啊，呃你没有办法直接minimize $P_{\theta }(x)$，我们通常真正minimize是什么，$P_{\theta }(x)$的一个lower，lower，它的一个下界啊，等下等一下在接下来的投影片里面，$\theta$通常都会被省略掉。

那我们来看一下在dd p m里面呢
这个$P_{\theta }(x)$是怎么被计算出来的呢

所以这个假设他只是一个假设而已，它并不完全合理，那你说那我们应该弄一个更复杂的distribution啊，不要说这个output就是一个guassian distribution啊，也许可以考虑更复杂的东西，而且这边我们都只考虑了mean，还没有考虑方差，怎么说，假设这个高斯每个dimension variant都是固定的，所以说能不能够把variance考虑进来的可以，但是过去的文献都告诉你说做出来不会比较好，就是所以这个假设是啊，现在你看到多数的模型va e呀，d d p M啊，都是用这个假设，就直接假设说输出是一个高斯的mean，他确实太过简单了，但是你用比较复杂的model做出来不会比较好的，然后接下来很多人会问的问题就是哎，那为什么是高斯呢，为什么不是别的玩意儿呢，跟你说，那当初假设别的玩意，你也会问同样的问题呀，哟这个这个用高斯还是有一些理由的，你会发现说中间有一些推导，如果这个不是高斯的话，你可能会呃保不定他这样
注意第一个P没有下标$\theta$,因为第一个$X_T$是sample出来的，和network没有关系

其中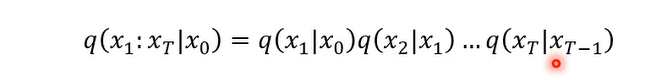

原理剖析3

这q($x_t|x_{t-1}$)怎么算呢

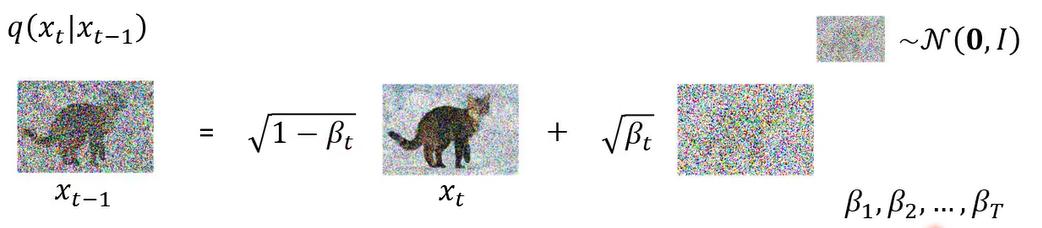
你先有一张图叫做x t等等，前面的乘上根号一减贝塔t，那这个贝塔t呢是事先准备好的值了，你会先定一个值，叫你会先定义一串值，叫做贝塔1到贝塔T，就是你要事先定好，那这个东西有点像是hyperparameter，你可以调啊，贝塔t代表在每一步的时候，我们的noise呢要加多大加多大，那这个noise呢是从一个mean零，，variance是1的一个高斯distribution sample出来的

其实q($x_t|x_0$)是可以直接算出来的

看看怎么做的

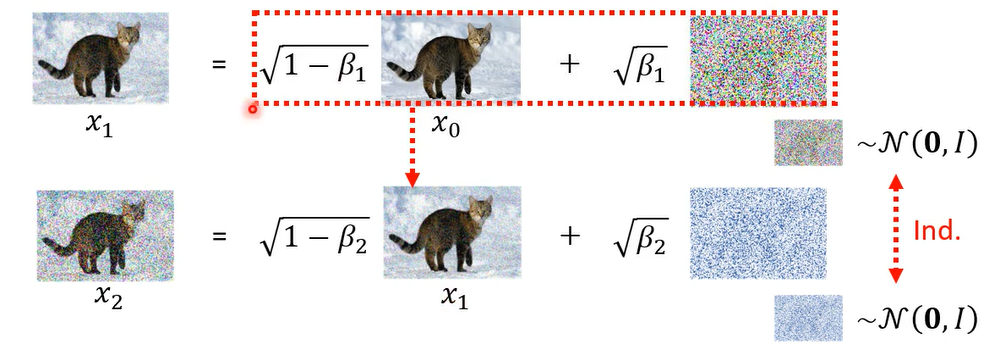
那这两个noise simple的过程，他们是independent，他们是从同样的distribution sample出来，但是这两次的simple是独立的。那接下来呢我们可以把x 1带到这里面

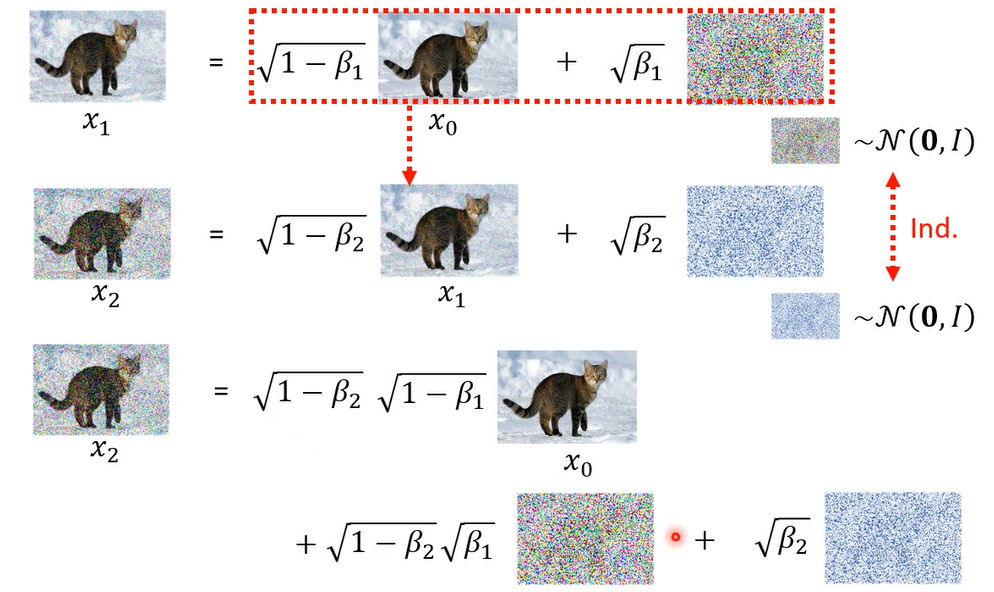
从同一个高深distribution sample两次，再乘上两个不同的weight加起来
，这一个distribution可以把它简化成只simple一次，前面乘另外一个不同的weight，

所以从高斯distribution里面，simple两次前面分别乘上这两个weight，它产生出来的distribution等同于从同一个高深distribution to sample一次。所以x2就等于

以此类推

本来我们以为从x0 到x t，你要就是做一次simple，一次simple，一次simple，总共做t次simple，你才会得到它，但是其实这整个过程就是一步到位就好，就做一次simple就可以产生x t

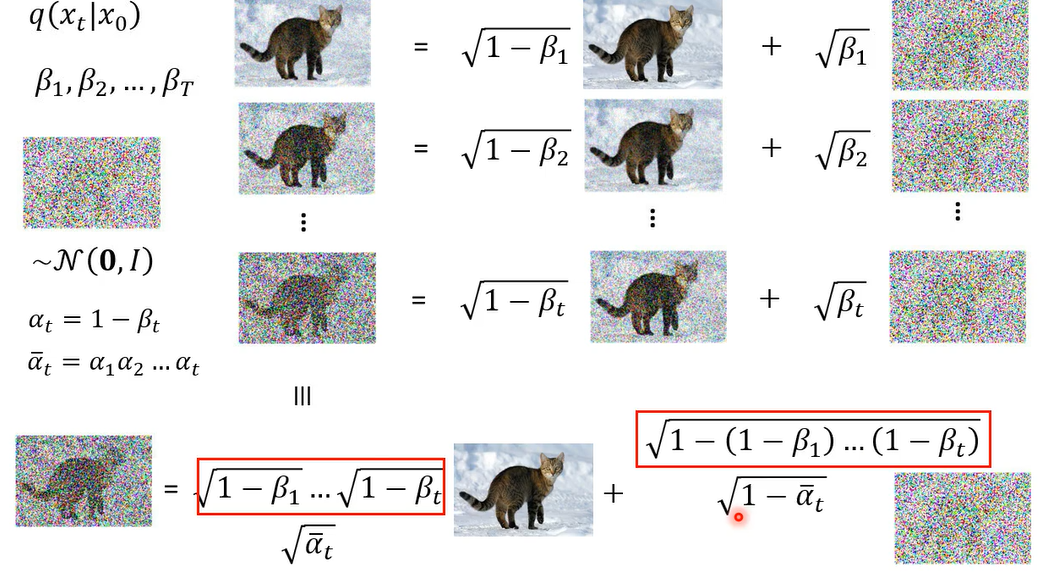
那我们这个这一项啊，是我们真正要minimize的lower bar，接下来你要把它经过一番整理，变成你可以算的样子

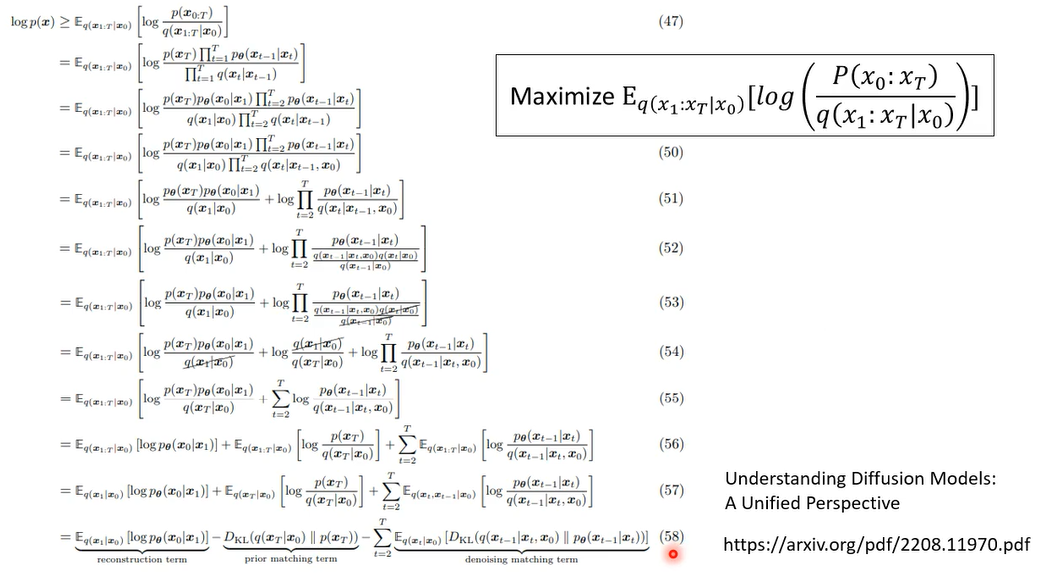
我们把最后一行放大一点

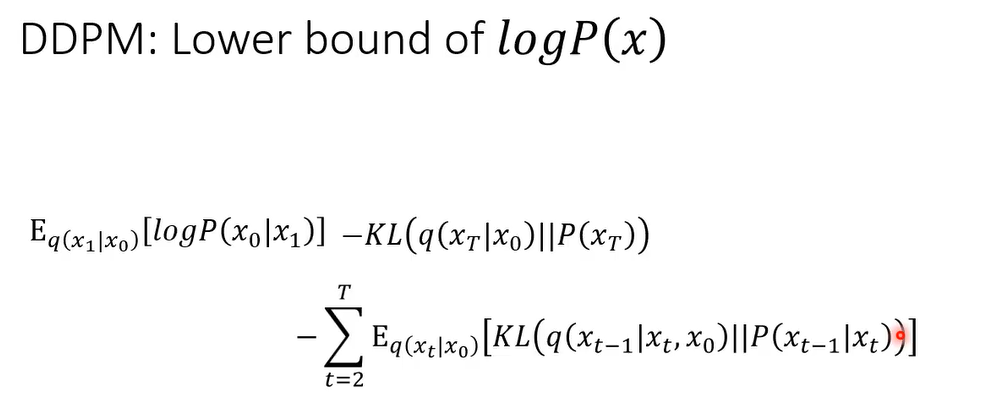
第二项和network没关系，第一项和最后一项计算类似，这里只看最后一项

蓝色框怎么算，q($x_t|x_0$)和q($x_{t-1}|x_0$)以及q($x_t|x_{t-1}$)你都知道怎么算，但是蓝色框内怎么算

现在是给你$x_0$和$x_t$求中间的$x_{t-1}$

这个式子可以经过一番化简，刚好成为你知道的那三个式子

这三项都是高斯distribution，这三项的mean你也都知道，这三项的mean跟variance你也都知道，但是把这两个distribution相乘，再除个东西到底长什么样子，接下来呢这个也是不适合做成投影片的

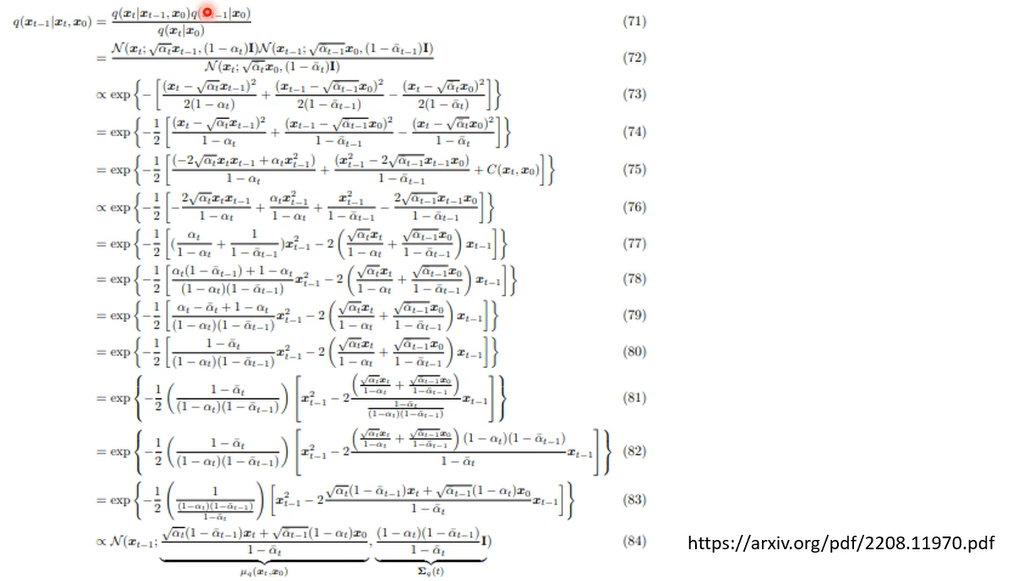
在文献上的就是你看这篇overview，经过一番疯狂的倒推以后，就是因为这三个distribution你是知道的，你知道他们的probability density function长什么样子，带进去硬推，硬推完以后，它的结果呢就是它仍然是一个高斯distribution，这高斯distribution的mean跟various分别长成这个样子

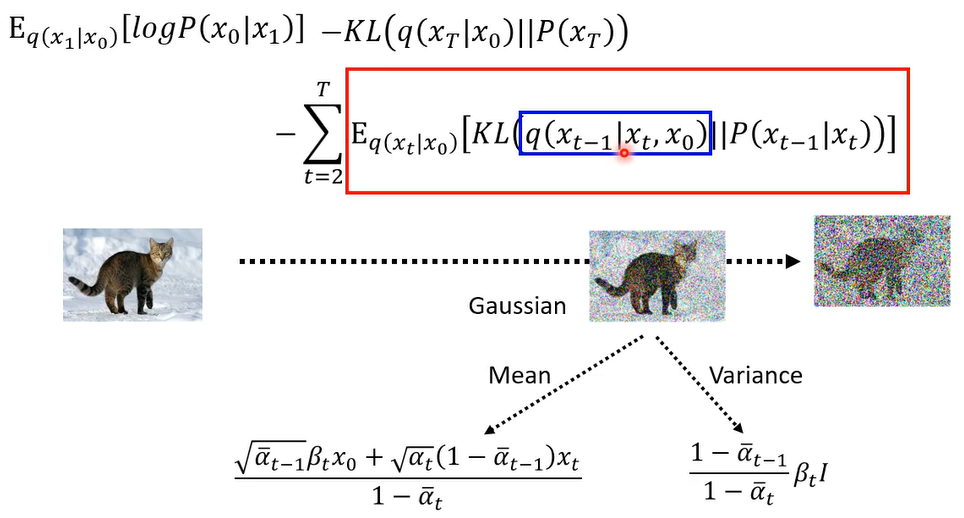
等于就是把x0 和xt做interpolation，哎所以这听起来感觉这个还蛮合理的啊

我们要计算的是这两个distribution kl divergence，那两个高选distribution kl divergence是有公式解的，那把公式解放在下面，理论上，你就你知道这两个高深distribution，你也知道他们的mean跟variance套以下公式，你是可以计算他们，但是呢，其实你是可以用更简单的方法，把这个kl divergence计算出来的

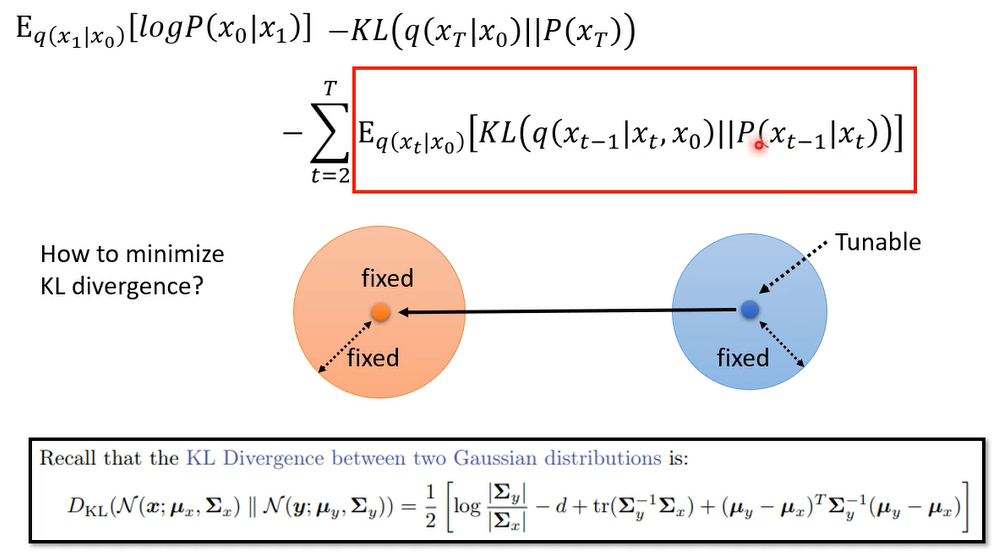
因为我的目标就是要mini这个kl divergence，而左侧是一个高斯distribution ，mean和variance是固定的，而右侧它是由你的network来决定的，由你的denoise的model来决定的，但是他的variance也是固定住的，我们根本就不考虑那个the denoise model 的variance，就假设它output的那个高清distribution，variance 每个dimension都是个定值，不不讨论他，那其实也有文献试图讨论他，但你好不了多少就是了，所以不讨论他的variance ，我们只考虑他的mean，他的mean倒是可以动的，因为它的面是取决于我们的denoise那个model，那如果我们要让这两个高斯distribution，他们的kl divergence越接近越好，那你唯一让他们为了接近越好，方法是不是把他们两个的mean让他越接近越好

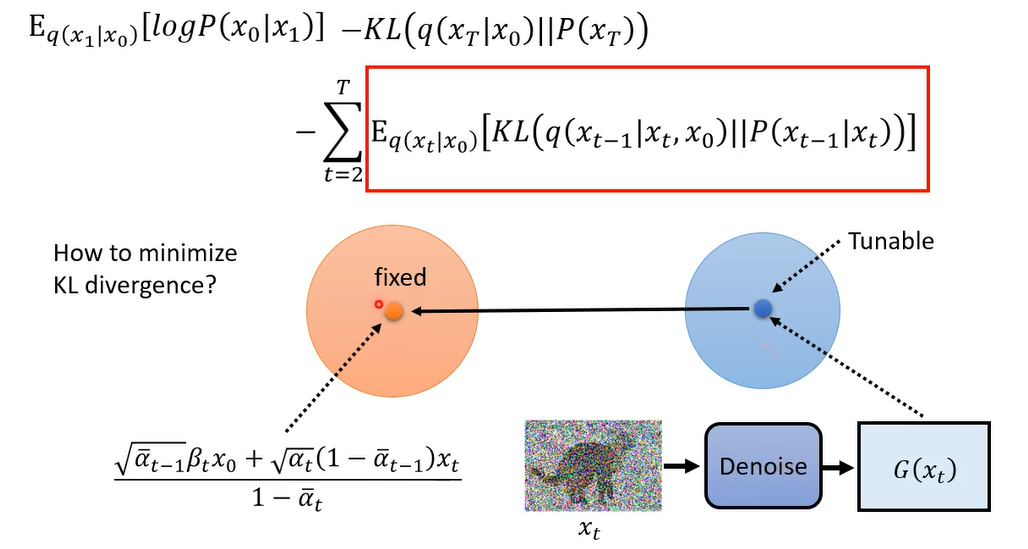
这个mean呢它是从denoise的model跑出来的，把x t丢进去看看我们会输出什么东西，输出来的东西就是P($x_{t-1}|x_t$)的mean，我们要让这两个mean越接近越好，左边它是固定的，所以实际上我们做的事情就是train这个denoise的model，让他们越接近越好。那实际上这一项到底要怎么minimize呢
它minimize的过程是这个样子的

因为前面这边的expectation
这边呢有一项是$q(x_t|x_0)$
所以x0 呢是先给定的，给定x0 的状态下呢
x t它其实是一个distribution啊
你把x0乘一个系数
加上$ϵ$乘一个系数得到x t啊

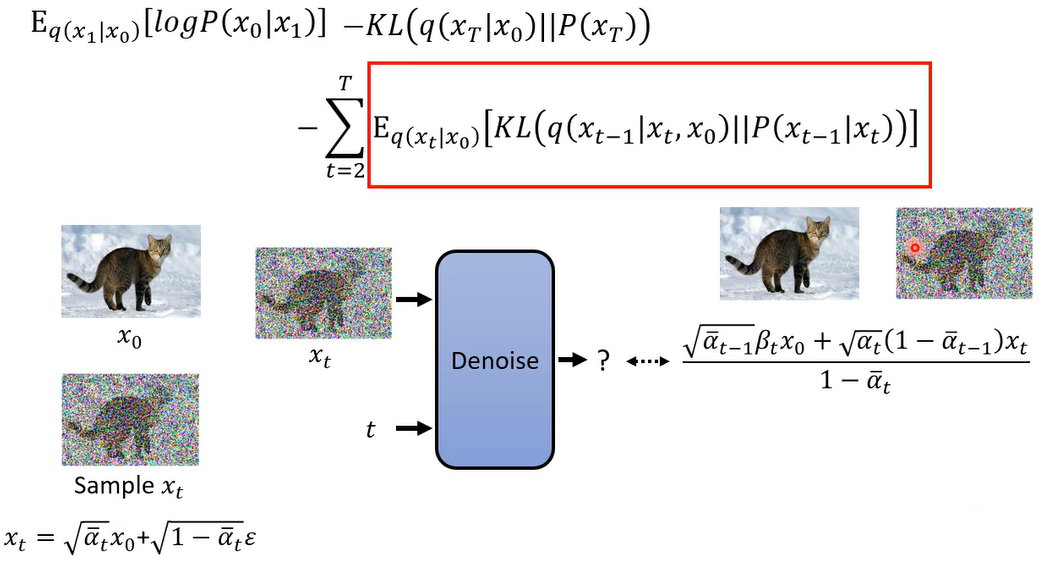
呃接下来你的denoise model
要做的事情就是吃一个xt,吃一个t,它output的结果要跟 q($x_{t-1}|x_t,x_0$) 的mean越接近越好

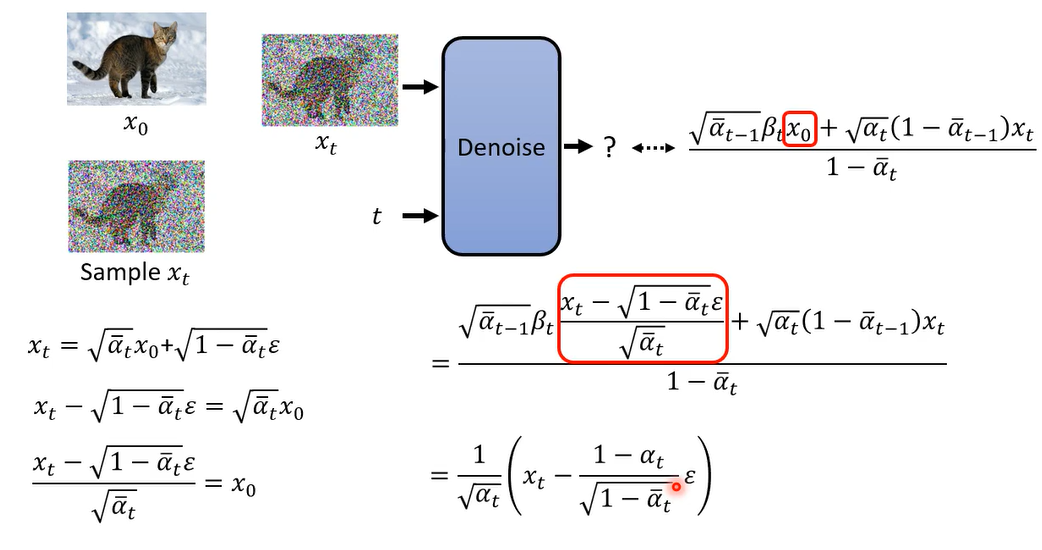
因为我们知道xt和x0的关系，所以还能进一步化简。

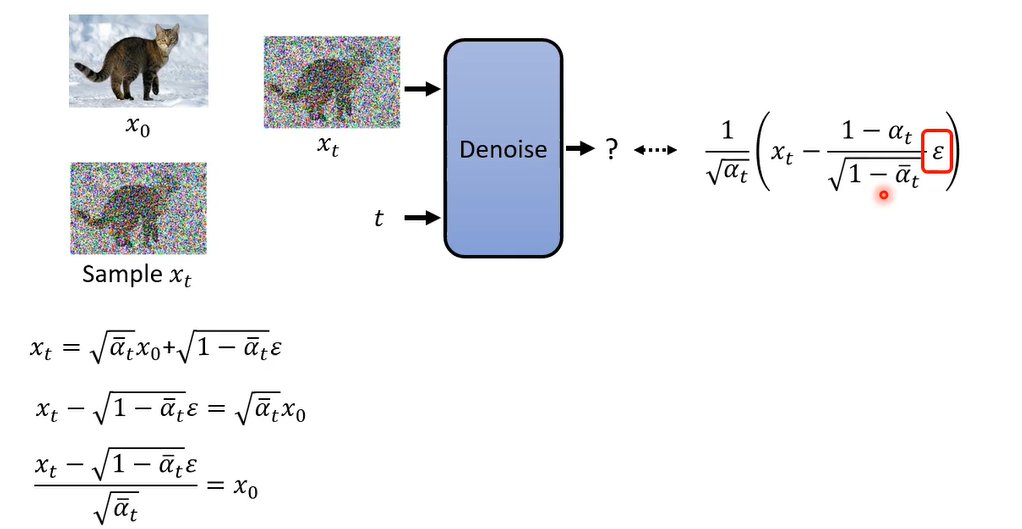
所以说那在这个他要输出的目标里面
其实只有$ϵ$是真正需要去predict，network真正需要去predict的只有$ϵ$，其他的阿尔法还有阿尔法拔都是常数

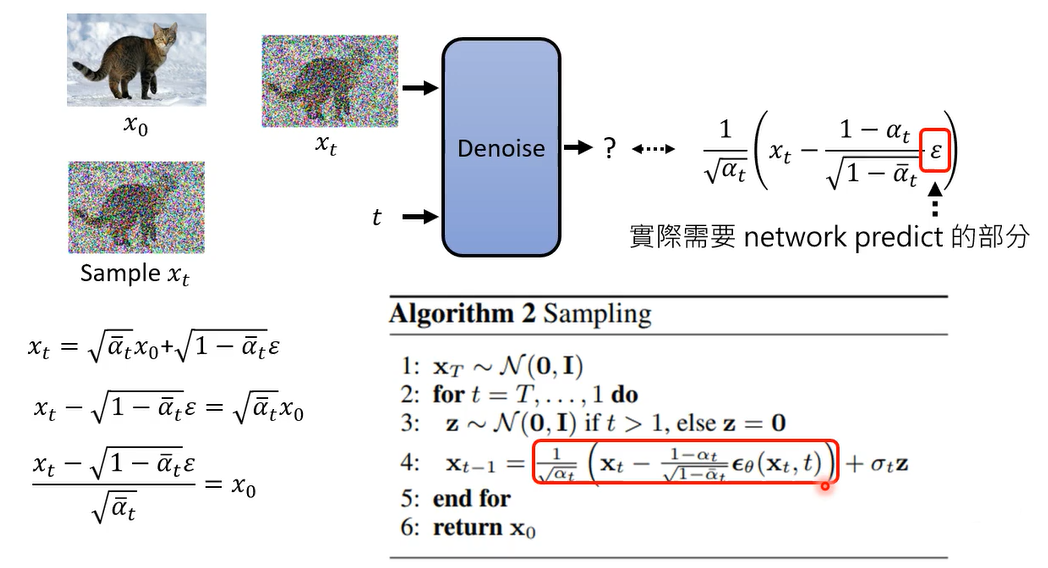
所以network唯一需要预测的就是加到x t里面的，那个noise就是$ϵ$，所以你会发现说这个式子就跟sampling的时候的，那个式子是一模一样的

阿尔法就当做是一个你事先设好的，hyperparameter好，然后你说哎那我如果我就是心情好，我想要劝一下阿尔法可不可以呢，其实d d p n的paper没开始有写，他说他们试图train了一下阿尔法，结果没有比较好哦，所以之后都不要管那个阿尔法了

就是在d d p m里面呢，它有一个schedule的process，就是这个阿尔法是谁决定的呢，这个阿尔法是被他决定的，记不记得我们前面在讲的时候，我们是说这个阿尔法t就是一减贝塔t嘛，所以你真的需要决定的是那个贝塔t，那贝塔t能不能认呢，呃可以learn，但是d d p n paper一开始就跟你说，哎learn的没有比较好，这样我就不learn了

所以你要用手设，那用手设怎么样比较好呢，啊他们里面给的一个建议，就是他们的那个贝塔是由小到大这样子啊，一开始是比较小的值，然后后来越来越大，但是那个增加的过程应该怎么设比较好呢，其实不知道他们就设一个这个利率增加的过程，那会有另外一篇paper，我记得如果没记错，他的title应该叫improve dd p a，那你就试着说啊，那是一个别的那个啊，贝塔的schedule，看会不会比较好，就试出一个比较好的schedule，所以这个有点像是hyperparameter是要调的

原理刨析4

但是讲到这里还没有解决的一个问题，就是为什么最后还要多加一个noise呢

当然你可能会说我们既然说这个dnoise，the module，它的output就是一个高斯的distribution,我们现在denoise的model真的算出来的只是高斯的mean，我们在sample的时候当然要加上一个noise，，代表说考虑当选的variance这一项

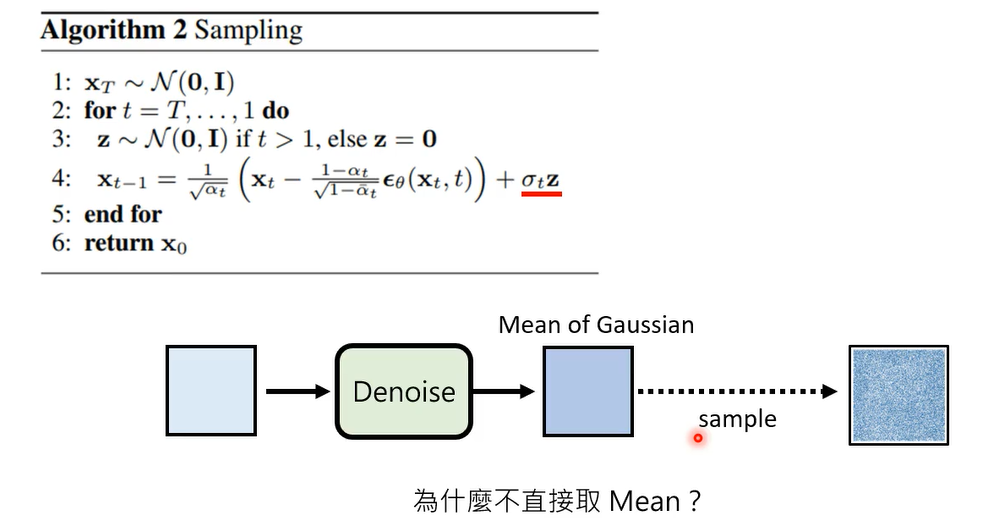
高斯取均值，也就是u的时候概率最大

先看一个类似的例子

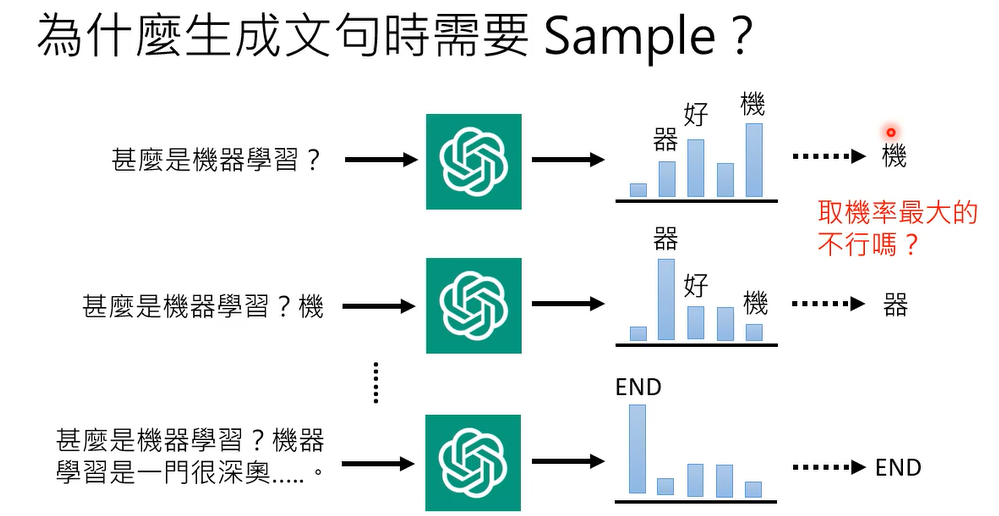
那有人可能会说这个取这个做sample的好处，就是你每次问同一个问题，chatgpt的答案都不一样，那为什么一定要这样呢，为什么不能固定住，就取几率最大的，但模型每次都回答几率最大的句子，这样不是也很好吗，有很多应用，你其实会希望说，你的模型的output每次都是固定的，为什么需要有随机性能，那其实这个问题过去就已经有人问过了，有一篇paper叫做the curious case of neural degeneration

那时候发现说如果你取几率最大的，你用你取几率最大的句子，每次你都取几率最大的词汇，你output的结果啊会是不断重复的句子，机器就会开始不断的跳帧，讲重复的话，虽然你做sampling，感觉机器比较会说一些奇奇怪怪的话，但是跟跳帧比起来，感觉simple的结果是比较好

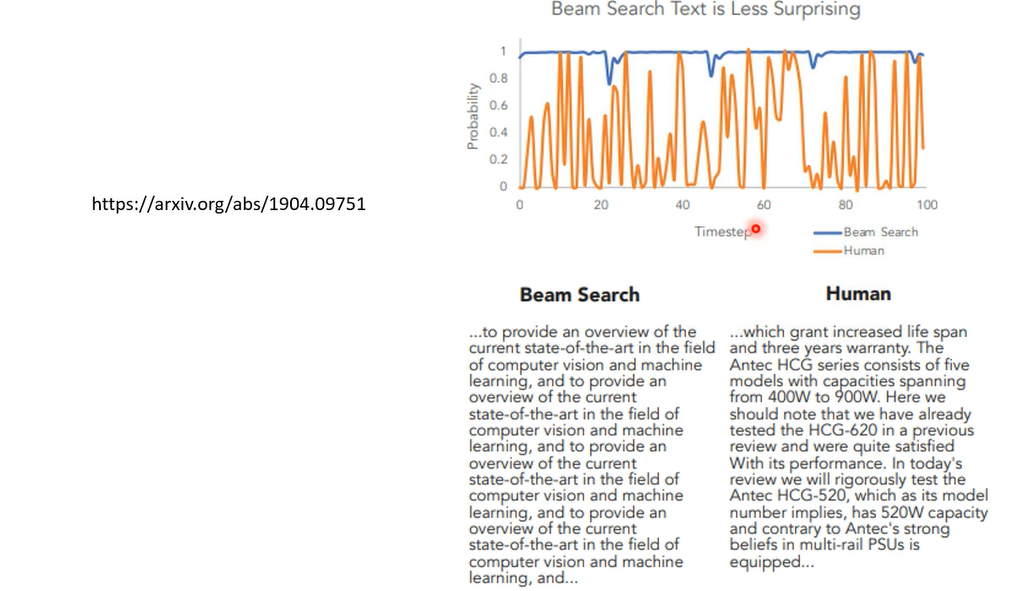
为什么呢，他做了一个分析，说我们来看看人写的句子吧，右边橙色这条线代表的是人写的句子，那右边是人写的一篇文章，我们来用我们的language model来计算，人写的这篇文章里面每一个字根据我们的language model，根据gp t two所计算出来的几率，你会发现说人写出来的文章，他用字遣词，并不是选几率最大的那一个词汇，那如果你看机器写的文章，他今天让机器选这个几率最大的词汇，让几率每当机器每一次产生字的时候，都产生几率最大的那一个字，那他发现说虽然这个句子机器产生出来的句子，它是几率最大的，但是它就是一个很奇怪的句子，你发现他不断重复在讲重样的话，the state of the art，the state of the art，一直讲一直讲，要反复讲，一样的话，当你在做生成的时候，几率最大的生成结果未必是最好的结果，那人在写一篇文章的时候，也许我们并不会选几率最大的词汇，选几率最大的词汇，他可能呃呃是最经典的，最常出现的词汇，但也是最无聊的，而且会反复出现同样的内容，这个是在文字上面的观察，但其实在语音上也有一样的观察

那今天呢语音当然都是用呃语音的，语音合成的模型都是用end to end做的啦，直接输入文字输出音轨

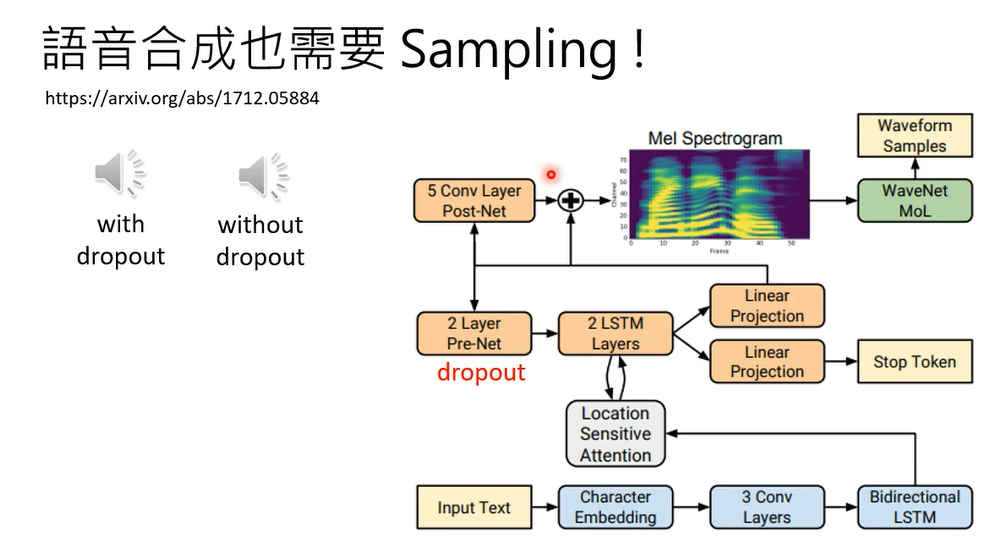
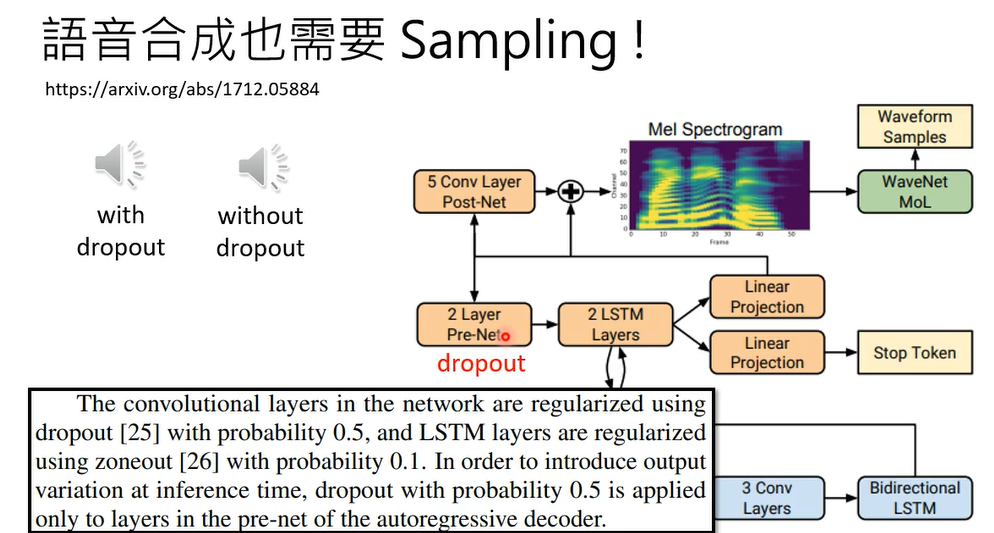
在testing加dropout。

所以会不会diffusion model也是同样的道理呢

实验验证后，也发现加noise是必要的

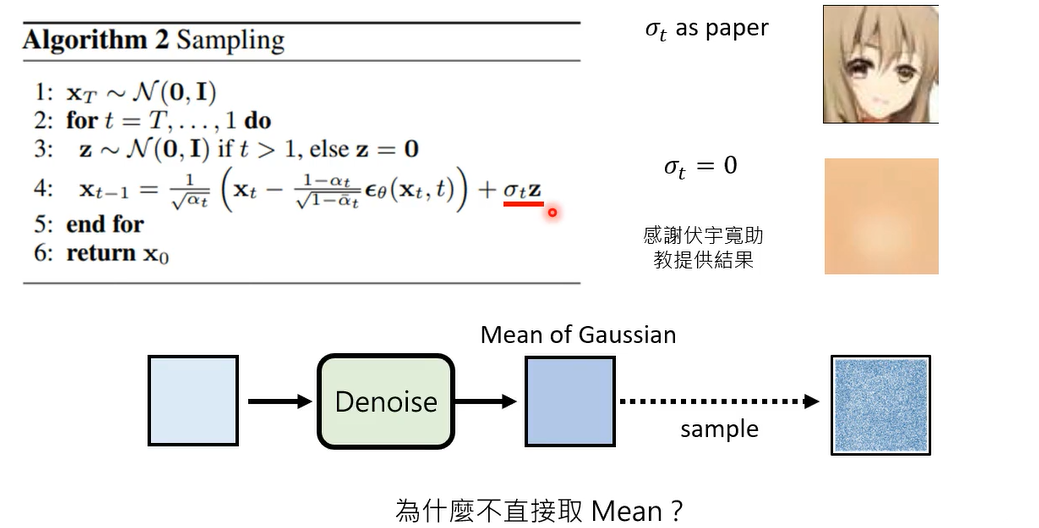
那这个就是diffusion model里面的玄机了啊

今天就告诉你说training的时候诶，为什么x为什么不是一次一次加noise，而是一步到位，加一次noise，就直接把它denoise掉呢，那这个我们已经讲过了
。然后呢也顺便讲一下，为什么在做simple的时候，我们是需要加noise

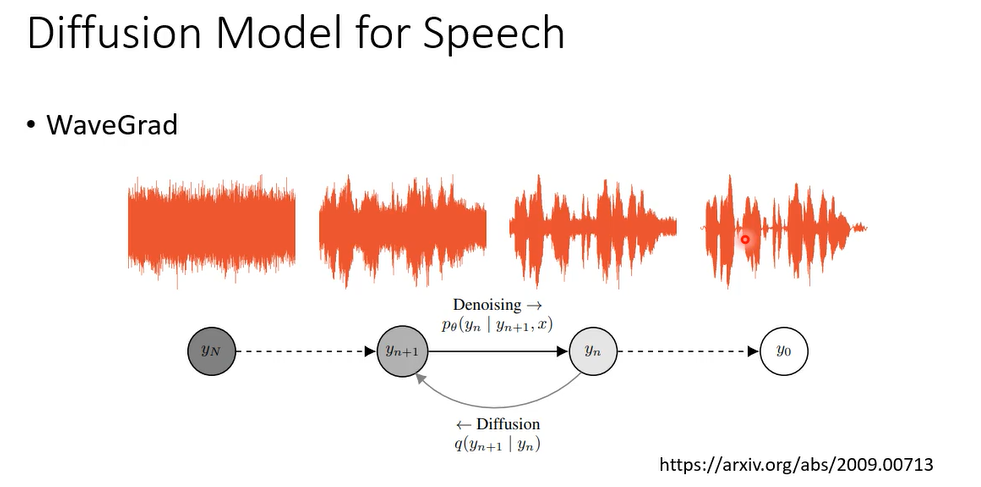
那这个diffusion model啊不是只能用在影像上，那在语音上也可以做diffusion model，做语音合成，这个就没有什么好讲的，跟影像上就是一模一样的啊，本来影像的input是2d的东西，把现在input变成1d的东西，你从一个完全高斯的simple的资讯，然后慢慢一步一步的做denoise，把它变成一段声音讯号，那就可以做语音合成。

但是把diffusion model坐在文字上就很麻烦了，至少你没办法直接apply DDPM，为什么没有办法直接派dd p m，你想我们今天做diffusion model的时候，我们就是希望说input image或input，一个一段声音讯号，你一直加高斯的noise，加到最后它就变成只有高斯的noise，没有其他的东西，看不出来原来是什么，但文字是discrete的东西，你没有办法把一个discrete的东西，一直加noise上去，让它变成完全是高斯，看不出来原来是什么东西。

一种方法是，我们今天就不讲细节，只讲大方向的概念，因为大方向的概念是不要把noise加在文字上，文字是discrete，没办法加noise怎么办哦，加在比如说加在word emdedding上，就这样结束了

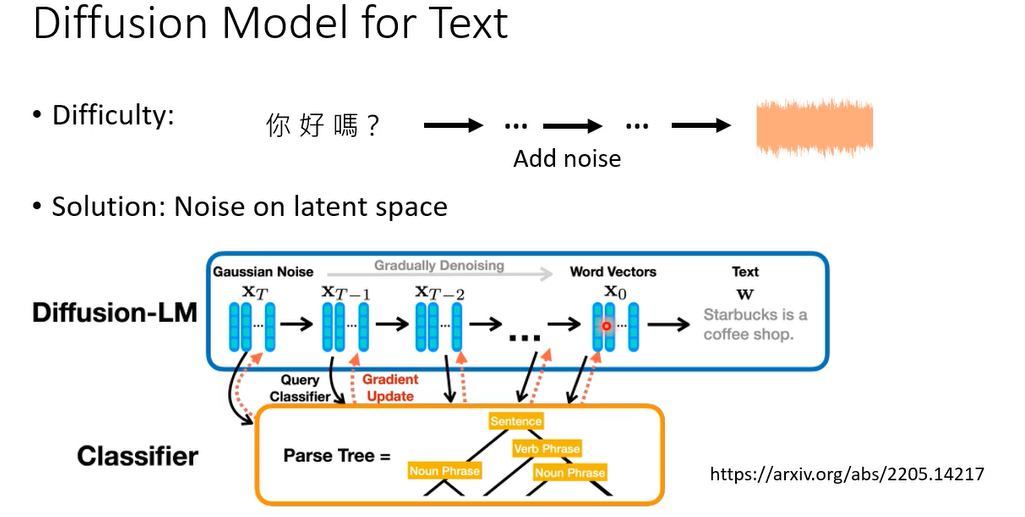
还有就是DiffuSeq

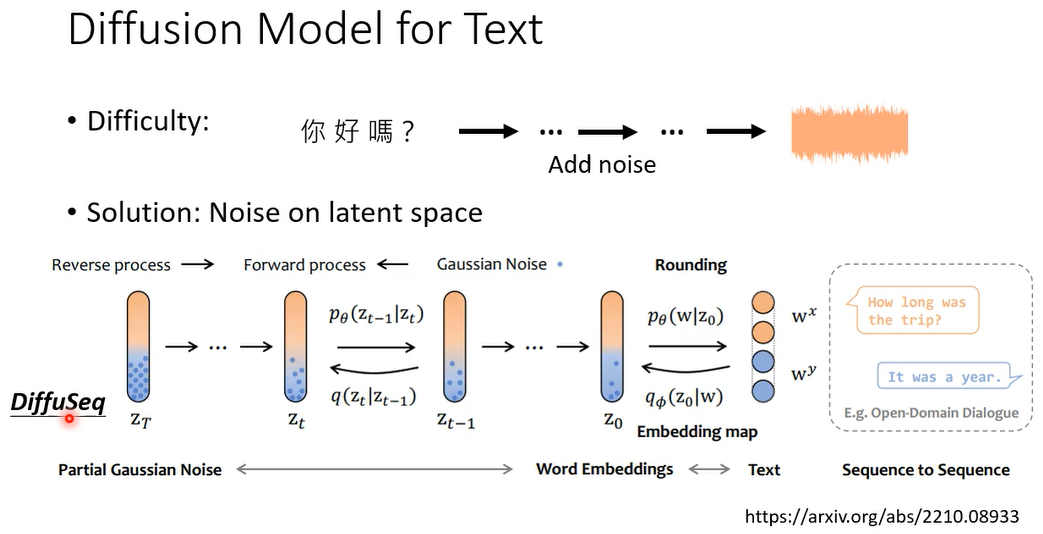
它是一个sequence to sequence和model啊，概念也是一样，反正就是在latent representation上面做这个diffusion

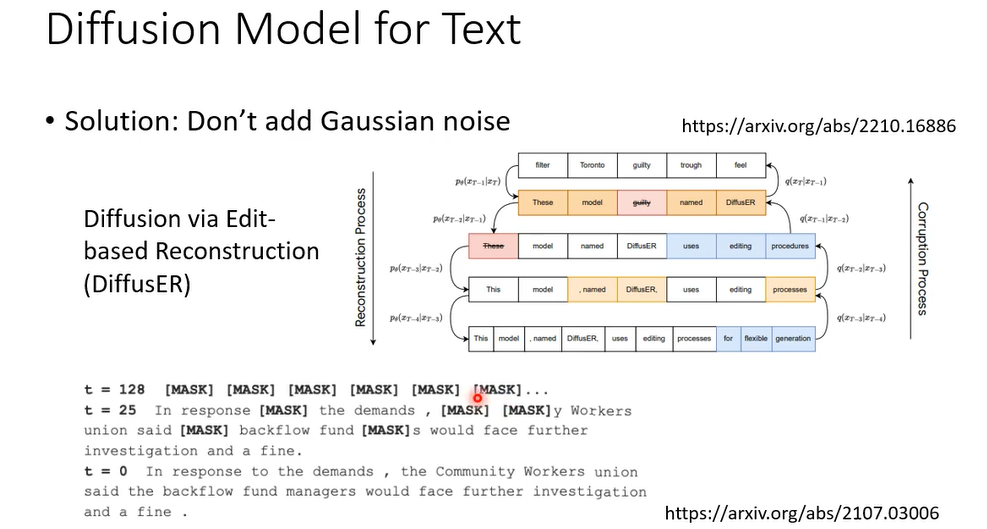
那还有另外的做法，这另外的想法是说，假设加高斯distribution，加高斯的noise是不行的，假设高斯，那也不能够加在文字中，discrete东西上，那能不能够想些其他的方法，其他种类的noise，其他种类的diffusion process加到文字上的，所以有另外一个系列的work，他们的走向就是把其他种类的diffusion process，加到文字上，所以他们到时候他们的这个这个noier distribution，就不是高斯，比如说这篇paper里面，他noise distribution都是全部都是mask，他们的这个xT呢是全部都是mask的句子，然后再慢慢的把有mask的地方呢填回来

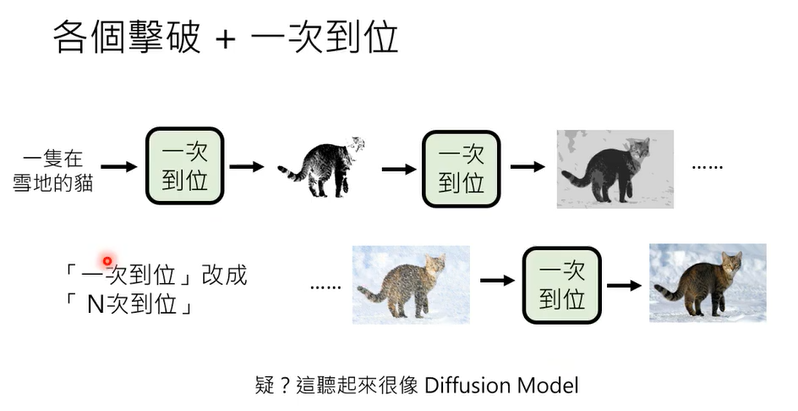
Diffusion Model的成功在于它将生成任务分解为多个小步骤（“n次到位”），借鉴了Auto-regressive Model逐步生成的优势，同时通过去噪的方式避免了Auto-regressive Model的一些局限性。这种分步生成的思想使得Diffusion Model在生成质量、稳定性和灵活性方面表现出色。

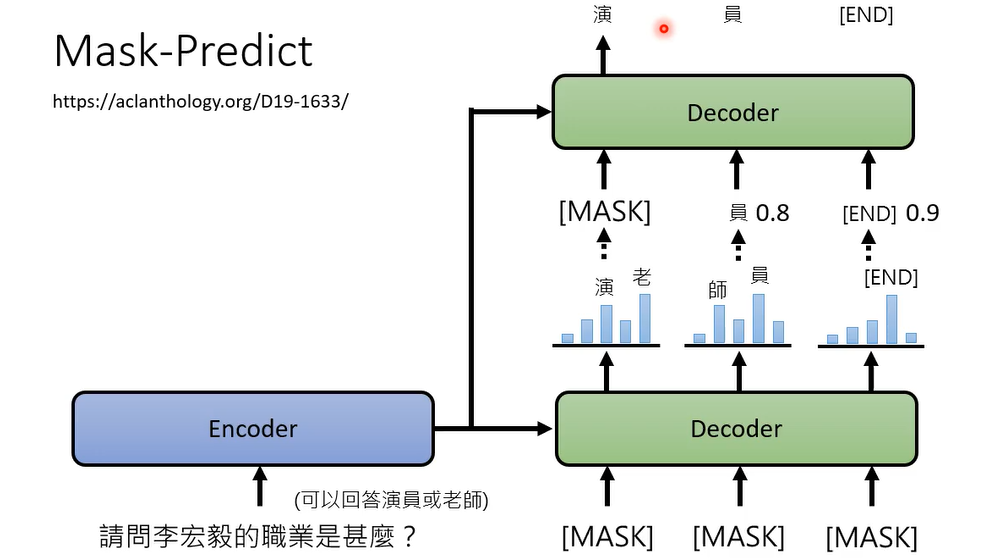
如果同样的输入可以有不同的答案,，那auto regressive model它可能会产生非常糟的结果,假设你有一个decoder，他是auto regressive是一次到位的一个model，就是输入给他一串mask，他把这些mask统统变成文字，那是因为他无法决定，到底答案应该是要演员还是老师，所以第一个字出现演跟老的几率都很大，然后第二个字出现师跟员的几率都很大，最后你做simple的时候，结果就会不好，那怎么办呢，有一个方法叫mask predict，如果今天第一次出现的结果不够好，那就再做第二次，把simple出来的结果里面几率比较低的，就你今天simple的时候，你会知道它原来的几率是多少吗，把几率比较低的部分用mask盖住，重新再做一次结果的生成

像这样的方法不只用在NLP上，也用在影像上

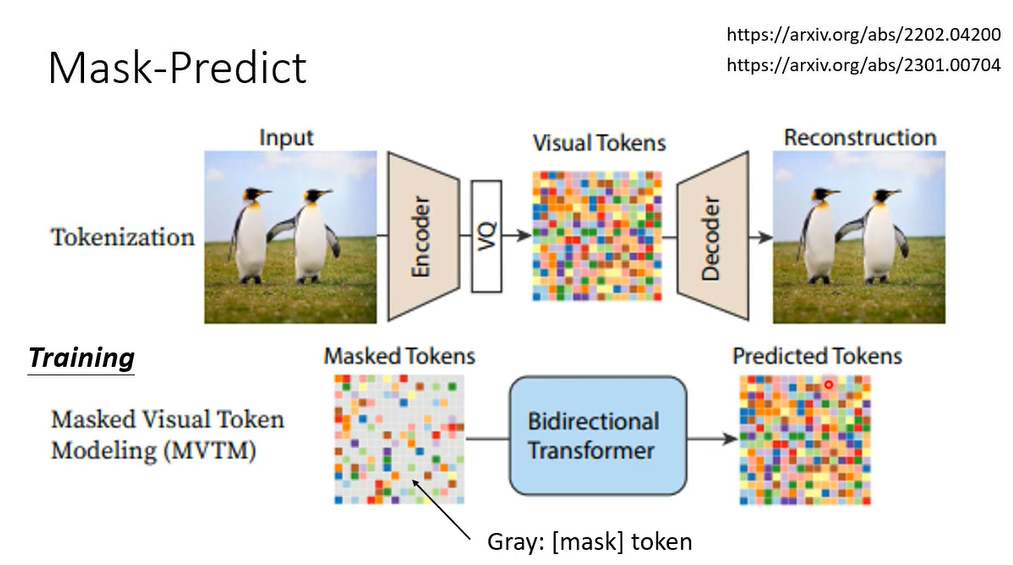
训练的时候把mask的部分猜回来，那生图的时候怎么做呢

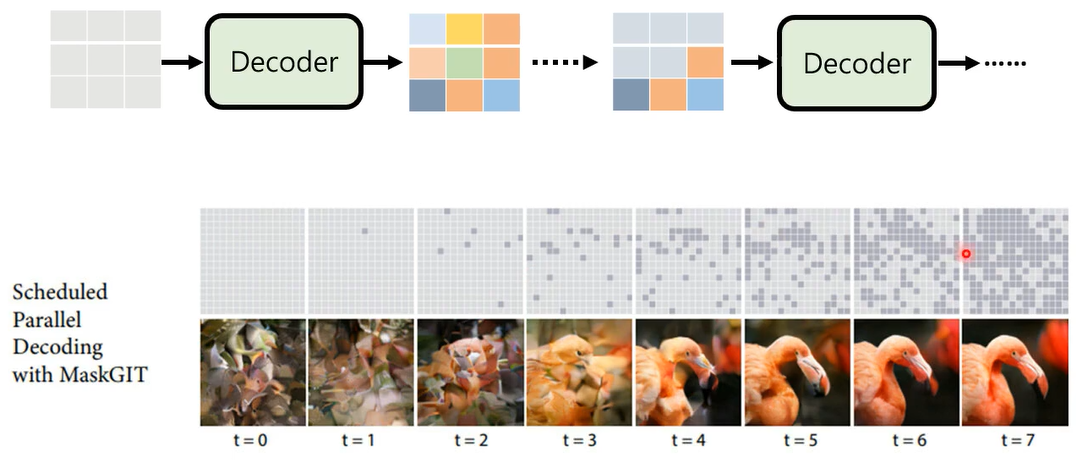
一开始你的图呢全部都是mask，把这个全部都是mask的图丢到decoder里面，decoder呢就产生一张图片，但是它产生出来的结果，里面的一些信息分数比较低的部分，把它再盖住，再重新mask，然后再重新生图，来用这个方法做也可以产生很好的结果

重点是把那auto regressive model加入
auto regressive的优势
这可能是diffusion model成功的关键

参考资料

李宏毅2023春机器学习课程